Оглавление:





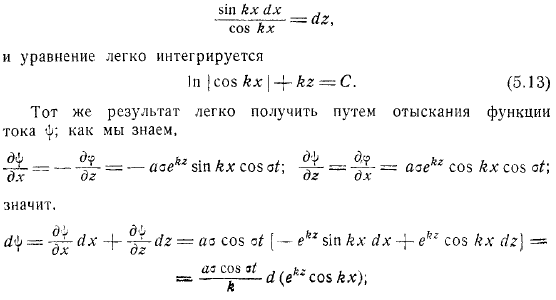
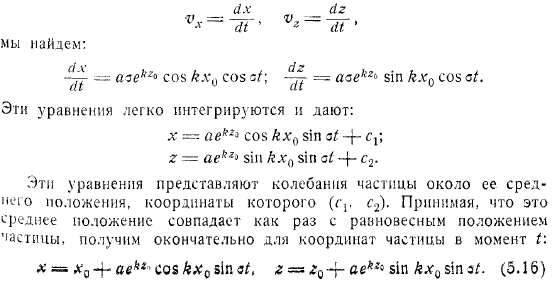

Стоячие волны
Сначала рассмотрим простейший случай. Если нет граней кроме вертикальной стенки гидромеханики, параллельной плоскости, которая еще не сыграла никакой роли, то пусть жидкость растекается в обе стороны и бесконечно (на самом деле это соответствует случаю очень большой глубины по сравнению с длиной волны). В этом случае можно легко найти конкретное решение системы уравнений вида.
Где означает постоянных значения. На самом деле, так как. Тогда мы получаем из уравнения. Если плоские волны мы решим это однородное линейное уравнение порядка с постоянными коэффициентами, мы получим. Любая константа должна считаться равной нулю.
- В противном случае, если абсолютное значение очень большое, то есть глубина большая, то термы будут очень большими (так как ось будет вертикально направлена вверх, то следует учитывать только отрицательные значения).
- Однако обе производные координат, то есть составляющая скорости, бесконечно возрастают в недопустимой. Те средства.
Теперь давайте посмотрим, что дает уравнение. Людмила Фирмаль
У нас есть. Итак, при любом мы вычисляем его по формуле. Тогда формула, имеющая любую постоянную прогрессивную волну , определяет потенциал скорости движения плоской волны неограниченной жидкости. Заметим, что здесь, в силу линейности системы фундаментальных уравнений, сумма решений любого числа этой системы также может быть решением системы.
Это утверждение будет использоваться неоднократно в будущем. То есть сначала изучают движение, которое определяется формулой, а затем изучают движение, которое определяется потенциалом скорости, который является суммой или более представлений формы. Рассмотрим движение с возможностью увеличения скорости.
- Для простоты рассмотрим, то есть движение с потенциалом скорости. Во-первых, найти форму свободного. To для этого используйте следующую формулу.
- В какой-то момент поперечное сечение поверхности жидкости в плоскости, параллельной плоскости, представляется таким образом.
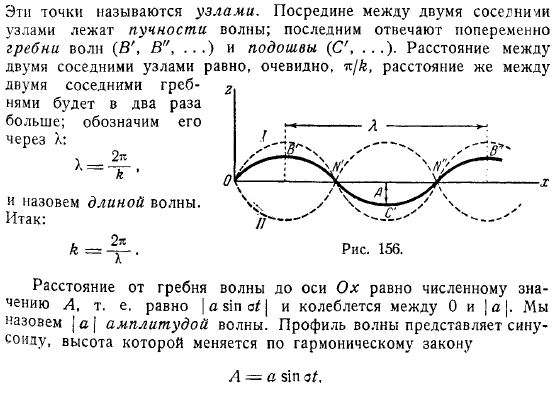
Синусоидальная волна. Если задать его на некоторое время, то уравнение синусоиды примет вид. Эта синусоида пересекает ось в точке с координатами. Чтобы было легче указать. Эти точки называются узлами. В середине соседних узлов есть волнистый живот волны.
Последние попеременно соответствуют размахивающей головке и подошве. Людмила Фирмаль
Расстояние между соседними узлами такое же, как расстояние между соседними хребтами, явно в раза. Мы покажем это следующим образом. Он называется. Расстояние от волнового фронта до оси равно числу, то есть равно или изменяется.
Мы называем это амплитудой волны. Профиль волны представляет собой синусоидальную волну, высота которой изменяется в соответствии с правилом гармоник. Таким образом, профиль волны вибрирует между крайними положениями.
Период этого колебания четко следующий: его называют волной. Обратная выражает частоту в единицу времени. Называется частота колебаний. Существует тесная связь между длиной волны, выраженной формулой, и периодом, который можно переписать следующим образом.
Далее мы переходим к рассмотрению скоростей и орбит различных жидких частиц. Прежде всего, определите проекцию скорости, но это по формуле. Напишите дифференциальное уравнение для линии потока. Где переменные разделены.
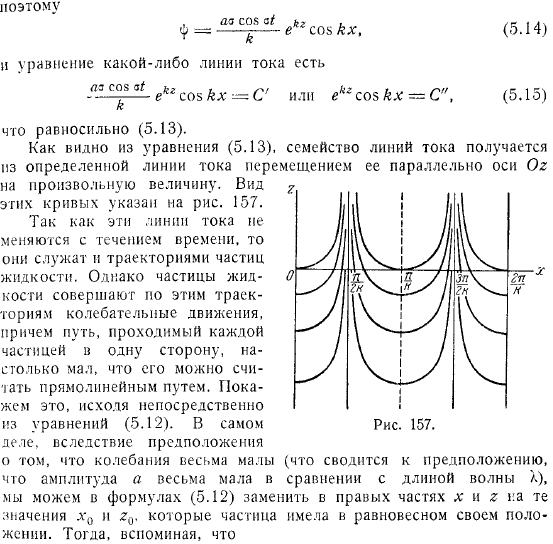
Уравнения могут быть легко интегрированы. Найдите текущую функцию и вы легко получите то же самое. Мы знаем. И уравнение обтекаемости. Это эквивалентно. Как видно из уравнения, семейство линий тока получается из конкретной линии потока путем перемещения параллельно оси при любом значении.
Внешний вид этих кривых показан выше. Поскольку эти линии тока не изменяются с течением времени, они также могут действовать как орбиты частиц жидкости. Однако частицы жидкости совершают колебательное движение по этим орбитам, и путь, по которому каждая частица движется в одном направлении, настолько мал, что его можно считать простым путем.
Исходим непосредственно из уравнения, обозначим. Факт, из-за предположения, что вибрация очень мала, амплитуда очень мала (это приводит к сравнению с предположением и длиной волны), которое может быть заменено правым выражением: значение и.
Частицы находились в равновесном положении. Мы найдем. Уравнение легко интегрируется и обеспечивает следующее. Эти уравнения представляют собой колебания вокруг промежуточных положений частиц, координаты которых являются центрами.
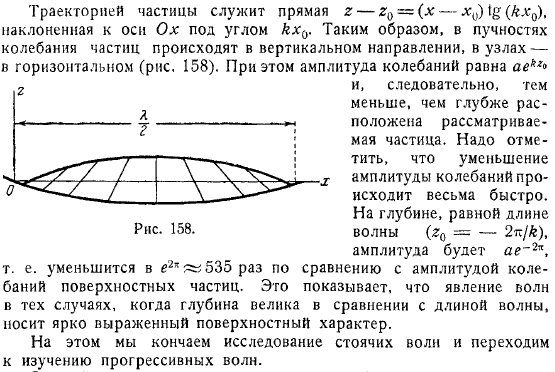
Если предположить, что это промежуточное положение совпадает с положением равновесия частицы, то в итоге получим координаты частицы в данный момент. Траектория движения частицы представляет собой прямую линию, наклоненную наискось к. На животе волны, вибрация частицы происходит вертикально, и на горизонтальном.
В этом случае амплитуда колебаний равна. Таким образом, чем глубже расположена рассматриваемая частица, тем больше она будет расположена. Обратите внимание, что уменьшение амплитуды колебаний происходит очень быстро.
На глубине, равной длине волны, амплитуда. То есть она уменьшается в разы по сравнению с амплитудой колебаний поверхностных частиц. Это свидетельствует о том, что явление волн в тех случаях, когда глубина больше по сравнению с длиной волны, имеет ярко выраженные поверхностные свойства. Исследование стоячей волны завершено, и исследование бегущей волны продвинуто.
