В этом пункте мы приведем несколько полезных утверждений о функциях, непрерывных на отрезке, которые мы будем использовать в дальнейшем.
Теорема Больцано-Коши (о промежуточных значениях). Пусть функция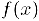 
непрерывна на отрезке 
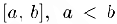. Тогда для любой точки С отрезка, граничными точками которого являются числа 
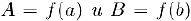. найдется точка 
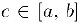такая, что 
.
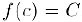Доказательство. Используем для доказательства метод дихотомии (деления отрезка пополам). Пусть для определенности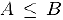 
. Обозначим через 
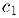. середину отрезка 
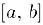Если окажется, что 
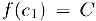, то 
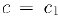и теорема доказана. Если же 
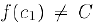, то обозначим через 
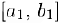отрезок 
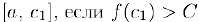и отрезок 
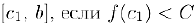. Таким образом 
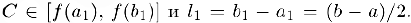Разделим далее отрезок 
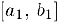точкой 
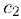. пополам. Если 
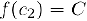. то искомая точка найдена. В противном случае обозначим через 
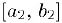отрезок 
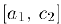. если 
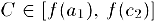и отрезок 
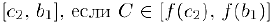. Здесь, очевидно, 
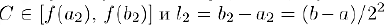. Продолжая этот процесс, мы либо через конечное число шагов найдем искомую точку 
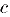, либо получим систему вложенных отрезков 
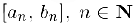. для которых
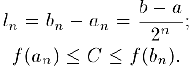
В соответствии с принципом вложенных отрезков (§2) существует общая для всех отрезков точка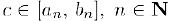 
. Из (1) следует, что с ростом n длины 
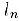отрезков 
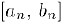стремятся к нулю, поэтому
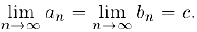
Ввиду непрерывности функции в точке с
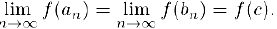
Отсюда, воспользовавшись (2) и свойством 5) предела последовательности (§3, пункт 2), получим, что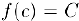 
. Теорема доказана.
Из теоремы Больцано-Коши вытекает важное в приложениях
Следствие. Если (функция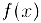 
непрерывна на отрезке 
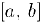и на концах этого отрезка принимает значения противоположных знаков, то внутри отрезка существует нуль функции, т.е. точка 
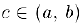, в которой 
.
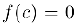Это следствие мы можем использовать для приближенного решения уравнения
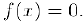
Чтобы избежать проблемы различения корней, будем считать. что внутри отрезка 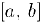существует единственный корень данного уравнения. Это последнее будет иметь место, например, если функция моно тонна на отрезке. Как следует из доказательства теоремы Больцано-Коши, для приближенного вычисления корня мы должны организовать процесс половинного деления отрезка, выбирая па каждом шаге тот из двух отрезков, па концах которого функция принимает значения противоположных знаков.
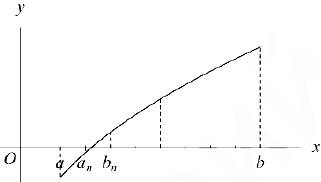
Если задана погрешность вычислений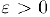 
. то остановиться мы должны на отрезке 
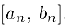, длина которого окажется меньше 
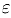, т. е.
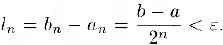
Из последнего неравенства следует, что
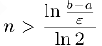
и, следовательно, закончить вычисления достаточно при
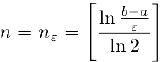
В качестве приближенного значения корня данного уравнения с точностью 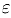мы можем взять середину отрезка 
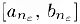. т. е. число
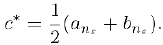
Сформулируем без доказательства еще две теоремы о непрерывных на отрезке функциях.
Теорема Вейерштрасса (о наименьшем и наибольшем значении). Непрерывная на отрезке 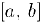функция 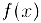) ограничена и достигает на этом отрезке своих нижней и верхней граней, т.е. найдутся точки 
такие, что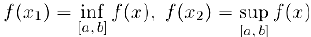 
.
Теорема (о непрерывности обратной функции). Непрерывная и монотонная на отрезке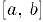 
функция 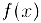имеет на отрезке, граничными точками которого являются числа 
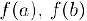непрерывную и монотонную в том же смысле обратную функцию 
.
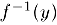Эта лекция взята со страницы онлайн помощи по математическому анализу:
Математический анализ онлайн помощь
Возможно эти страницы вам будут полезны:
