Свойства функций, непрерывных в ограниченной замкнутой области
Приведем свойства функций, непрерывных в ограниченной замкнутой области (они аналогичны свойствам непрерывных на отрезке функций одной переменной — см. п. 19.5). Предварительно уточним понятие области.
Областью называется множество точек плоскости, обладающих свойствами открытости и связности.
Свойство открытости: каждая точка принадлежит ей вместе с некоторой окрестностью этой точки.
Свойство связности: любые две точки области можно соединить непрерывной линией, целиком лежащей в этой области.
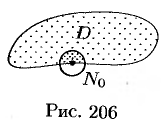
Точка 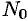 называется граничной точкой области
называется граничной точкой области 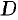 , если она не принадлежит
, если она не принадлежит 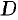 , но в любой окрестности ее лежат точки этой области (см. рис. 206). Совокупность граничных точек области
, но в любой окрестности ее лежат точки этой области (см. рис. 206). Совокупность граничных точек области 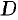 называется границей
называется границей 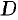 . Область
. Область 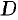 с присоединенной к ней границей называется замкнутой областью, обозначается
с присоединенной к ней границей называется замкнутой областью, обозначается 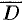 . Область называется ограниченной, если все ее точки принадлежат некоторому кругу радиуса
. Область называется ограниченной, если все ее точки принадлежат некоторому кругу радиуса 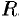 . В противном случае область называется неограниченной. Примером неограниченной области может служить множество точек первого координат кого угла, а примером ограниченной —
. В противном случае область называется неограниченной. Примером неограниченной области может служить множество точек первого координат кого угла, а примером ограниченной — 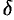 -окрестность точки
-окрестность точки 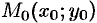 .
.
Теорема 43.1. Если функция 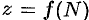 непрерывна в ограниченной замкнутой области, то она в этой области: а) ограничена, т. е. существует такое число
непрерывна в ограниченной замкнутой области, то она в этой области: а) ограничена, т. е. существует такое число 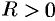 , что для всех точек
, что для всех точек 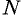 в этой области выполняется неравенство
в этой области выполняется неравенство 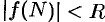 ; б) имеет точки, в которых принимает наименьшее
; б) имеет точки, в которых принимает наименьшее 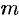 и наибольшее
и наибольшее 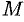 значения; в) принимает хотя бы в одной точке области любое численное значение, заключенное между
значения; в) принимает хотя бы в одной точке области любое численное значение, заключенное между 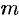 и
и 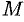 .
.
Теорема дается без доказательства.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Предел функции двух переменных |
| Непрерывность функции двух переменных |
| Частные производные первого порядка |
| Геометрический смысл частных производных функции двух переменных |
