Свойства функций, непрерывных в точке

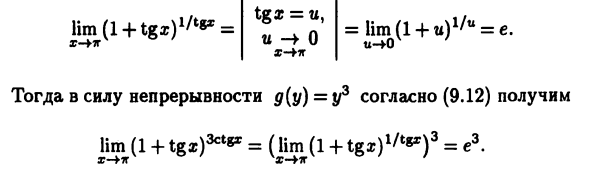
Свойства функций, непрерывных в точке

• Если функция f (x) непрерывна с a∈R, На данный момент, окончательный предел из-за свойств 1 и 2 (см. 7.4) Будет предложено, ограничено некоторыми районами } (A) φ0 — знаковая константа. Также из правил ограничения Переход (7.22) — (7.24) Арифметическая операция продолжается Непрерывность в a∈R: 1) Линейная комбинация конечного числа функций m∈N, Непрерывный в определенной точке, т.е. м 3 lim D (i) = D (a) € RV * = T to fH = «lim Y> * A (*) = x —►aa? -Fa * » фк = л да = V * c * lim Λ (x) = NL (a), c * € R V * = 1, м; (9,7) 2) произведение функции конечного числа m 6 N,

Непрерывный в определенной точке, т.е. 3 lim fk (x) = fk (a) e R V * = 17 ^ = * да 3) частное двух функций, которые являются последовательными в данной точке, Тем не менее, значение делителя в этой точке Ноль, то есть (3 лим. F (x) = f (a) e R) A (3 лим. G (x) = g (a) хм г (х) г (а) X + CL X- + CL Свойства (9.8) могут быть расширены естественным образом порядок n N N последовательных функций в 31im / (x) = / (a) € R => * lim (/ (s)) n = (lim f (x)) n = (/ («))». (9,10) I-й В частности, согласно (7.25) полином Строка R (кроме случаев, когда знаменатель Ноль.

Непрерывная функция в любой точке x∈R и дробное рациональное число Согласно (7.26) функция непрерывна во всех точках числа. Людмила Фирмаль

Теорема 9.1. Когда функция y = f (x) непрерывна в точках a, функция g (y) непрерывна в соответствующих точках Если 6 = f (a), комплексная функция g (f (x)) непрерывна в точке a. или (3 lim / (x) = f (a) = 6) A (3 lim g (y) = g (b)) = » X — Fe Y — F6 ^ 6 = Из-за непрерывности 0 3 0: | p (y) -e (b) \ 0 и все x удовлетворяют условию \ x-a \ <8iy, имеет место неравенство | / (x) -b \ <8, Поэтому для такого x выполняется условие \ g (f (x)) — g (b) \ <e. Последний является lim * (f (*)) = g (b) = g (M), (9.11) То есть, согласно определению 9.1, комплексная функция £ (/ (#)) Непрерывный с Пример 9.3. Функция cosx = sin (x + 7r / 2) Каждая точка x∈R как суперпозиция согласно теореме 9.1

На основе непрерывной функции y = f (x) = x + η / 2 ( Свойство непрерывности непрерывной линейной комбинации (9.7) Function) и g (y) = sin y (см. Пример 9.1). Tgx = функция = (Sin x) / cosx по (9.9) как частное от непрерывной функции Непрерывно в тех точках x∈R, где cos zΦ0, т.е. непрерывно Все xΦb + tr / 2 (k∈Z). Аналогично, функция ctgx = = (Cosx) / sina; непрерывно в тех точках x∈R, где sinx / 0, То есть все xΦkn (k € Z). # Отметим, что теорема 9.1 может быть обобщена Наложение 3 или более функций. Справа от (9.11) находится значение аргумента / (а) Выражается через пределы функции f (x) функции g (y), NT * (/ («)) =» (Это /(•))•(9.12) х- \ а Следовательно, для непрерывных функций, операция

• Переходные ограничения пермутируют с операцией для расчета Значение функции соответствующей точки. Согласно теореме 9.1 Полезно при вычислении пределов сложных непрерывных функций Подставьте эти операции. Отношения (9.12) Рассматривается как частный случай теоремы 7.6 о пределах комплексных чисел Работает, когда внешняя функция g (y) непрерывна. В этом случае часто называют признаком ограничений и продолжения Вы можете изменить порядок функций.

Рассчитать на основе примера 9.4 (9.12) Представляет функцию под символом ограничения формы Думайте об этом как о суперпозиции функции y = f (x) = = (L + tgx) 1 / * 8 * и g (y) = y3. Создание замены w = tgs Легко вычислить lim f (x). Конечно дано Второе заметное ограничение (см. (7.42)) TGX = и Z- ¥ ir Тогда непрерывность дает g (y) = y3 согласно (9.12). lim (1 + tgs) 30 ^ = (lim (1 = е3.

Смотрите также:

Предмет математика

Признаки существования предела действительной функции	Односторонняя непрерывность. Точки разрыва
Непрерывность функции в точке	Свойства функций, непрерывных в промежутке