Теоремы о среднем для дифференцируемых функций
В математическом анализе большое значение имеет группа теорем о существовании внутри интервала, где функция дифференцируема, точки. в которой производная обладает определенными свойствами.
Теорема Ролля. Пусть функция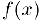 
дифференцируема в интервале 
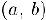, непрерывна на отрезке 
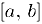и на концах этого отрезка принимает равные значения. Тогда внутри отрезка существует точка 
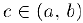, для которой 
.
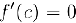Доказательство. По теореме Вейерштрасса (глава IV. §5. пункт 3) функция достигает на отрезке 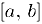своих наименьшего m и наибольшего M значений. Если 
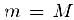, то 
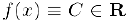. и в качестве точки с мы можем взять любое число интервала 
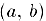, так как 
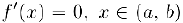. Если же 
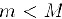, то по крайней мере одно из этих значений достигается внутри отрезка. Для определенности предположим, что 
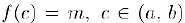и докажем, что точка с—искомая. Действительно, при малых приращениях аргумента 
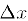в точке с имеет место неравенство 
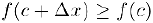, следовательно, 
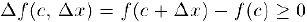и
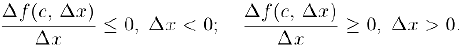
Отсюда, использовав дифференцируемость функции в точке с и свойство 5) предела функции (глава IV, §4, пункт 2), получим:
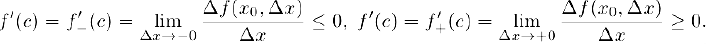
Таким образом.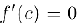 
, что и требовалось доказать.
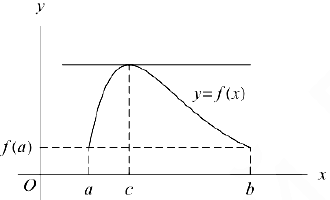
Геометрически доказанное утверждение означает, что на графике дифференцируемой функции между граничными точками, имеющими равные ординат ы, найдется точка, в которой касательная параллельна оси абсцисс.
Теорема Лагранжа. Пусть функция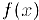 
непрерывна на отрезке 
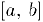и дифференцируема в интервале 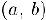. Тогда найдется точка с € (а, 6), для которой
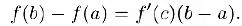
Для доказательства этой теоремы рассмотрим функцию
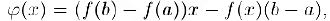
которая удовлетворяет всем условиям теоремы Ролля, так как опа, очевидно, непрерывна па отрезке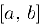 
, дифференцируема внутри его и 
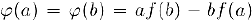. Тогда существует точка 
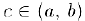, для которой 
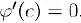. Так как
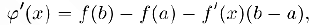
то
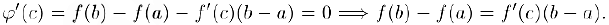
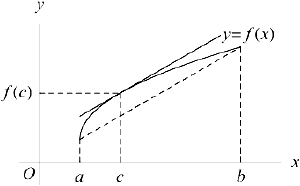
Геометрический смысл теоремы Лагранжа заключается в том, что между граничными точками графика дифференцируемой в интервале функции всегда можно найти точку, в которой касательная параллельна хорде, соединяющей граничные точки графика.
Теорема Коши. Предположим, что функции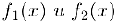 
непрерывны на отрезке 
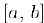и дифференцируемы в интервале 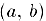. причем 
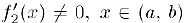. Тогда существует точка 
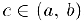, для которой
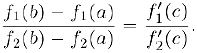
Теорема Коши может быть доказана совершенно аналогично предыдущей теореме, если ввести в рассмотрение функцию
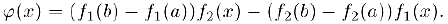
Теорема Коши имеет тот же геометрический смысл, что и теорема Лагранжа, если мы рассмотрим параметрически заданную функцию
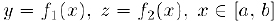
аргумента z. Графиком этой функции является линия в плоскости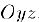 
. Хорда, соединяющая точки 
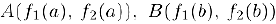имеет угловой коэффициент 
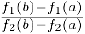а угловой коэффициент касательной к графику этой функции в точке 
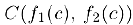равен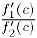 
(§2, пункт 2).
Тогда теорема Коши утверждает, что касательная к графику этой параметрически заданной функции в точке С параллельна хорде, соединяющей точки графика А и В.
Эта лекция взята со страницы онлайн помощи по математическому анализу:
Математический анализ онлайн помощь
Возможно эти страницы вам будут полезны:
