Теоретические основы и технологии начального математического образования - Семиотические аспекты обучения математике в начальной школе

Оглавление:

Распознавание начинается с момента возникновения проблемы. До тех пор, пока существование проблемы как знания о не-знании не признается, процесс признания не может начаться. Возникновение проблемы — это не только осознание того, чего мы еще не знаем, но и готовность искать ее решение. Возникновение проблемы обусловлено некоторыми предпосылками в виде предзнания, которое может быть как результатом действий человека в реальном мире, так и результатом воображения, необходимого для формирования идеи и возникновения на ее основе вопроса, поиск ответа на который составляет суть познания.

Познание в математике может представлять некоторые элементы как первичные исходные элементы, из которых можно построить теорию, обеспечивающую способ решения поставленной задачи. Геометрия, например, начинается с точки, линии, плоскости как начальных элементов. Абстрактные математические понятия «точка» или «линия» не имеют материального существования сами по себе и не обладают индивидуальными свойствами, но все, что можно узнать о точках и линиях, ограничивается тем, что видно в их взаимодействии с другими геометрическими объектами. Более того, описания вида «точка — это то, что не имеет ни размера, ни частей» ничего не определяют и нигде не используются в геометрии. Тем не менее, эти виды описаний играют психологическую роль; они необходимы как рамки отсчета для мысли, поскольку мысль не может быть беспредметной. И точка, и линия чаще всего представляются учащимся в виде графических моделей.

Возможен и другой подход к введению начальных когнитивных элементов в математику. Она заключается в том, что исходные элементы не задаются сами по себе, а берутся из системы, известной тем или иным образом из предыдущего опыта. Как показал Ж. Пиаже, оптологическая особенность математического познания заключается в том, что понимание абстрактных математических структур основывается на неявных знаниях, связанных с элементарными арифметическими и геометрическими понятиями, сформированными достаточно рано и независимо от направленного обучения. Обращение к таким представлениям позволяет нам рассматривать, например, точку как результат дифференциации и интеграции имеющихся у детей знаний об окружающем пространстве и твердых телах в этом пространстве, расположение которых можно зафиксировать каким-либо визуальным способом, а линия рассматривается как траектория движения объекта, особенно точки.

Однако математическое образование не может игнорировать онтологическую природу математических объектов, о природе которых существуют различные мнения, восходящие к Платону и Аристотелю. Например, Платон считал, что математические объекты существуют сами по себе, «в готовом виде», так сказать, в мире идей и обнаруживаются только благодаря интеллектуальным усилиям человека. Аристотель же считал, что математические понятия возникают в процессе конструктивной и преобразующей деятельности человека в реальном (вещественном или идеальном) мире и существуют в виде мысленных образов, которые «материализуются» через различные знаки. И Платон, и Аристотель отмечают абстрактность математических сущностей, поскольку как материальные объекты они представлены только знаками.

С методологических позиций знак (знак-форма, схема) является объектом действия. Более того, знаки в математике таковы, что обычно не допускают двусмысленности и позволяют нам обращаться с ними в соответствии с четко определенными правилами. Эта ситуация «провоцирует» педагогические усилия по обучению этим правилам. Знаки более «удобны» и «доступны», чем содержание, которое они представляют, и в условиях обучения они могут неоправданно доминировать над означаемым содержанием. В этом случае знак воспринимается либо как обозначение самого себя, либо как неотъемлемый атрибут объекта, представленного знаком. Например, «2» — это число два.

С другой стороны, математические понятия, правила, связи и отношения обычно представляются познающему субъекту не отдельными знаками, а текстами, которые обычно представляют собой последовательность слов или самих математических знаков. Например, метод нахождения суммы 7 + 5 может быть представлен следующим текстом: Найдите число, которое прибавляет 7 к 10, найдите число, которое прибавляет найденное число к 5, прибавьте полученное число к 10; запишите ответ.

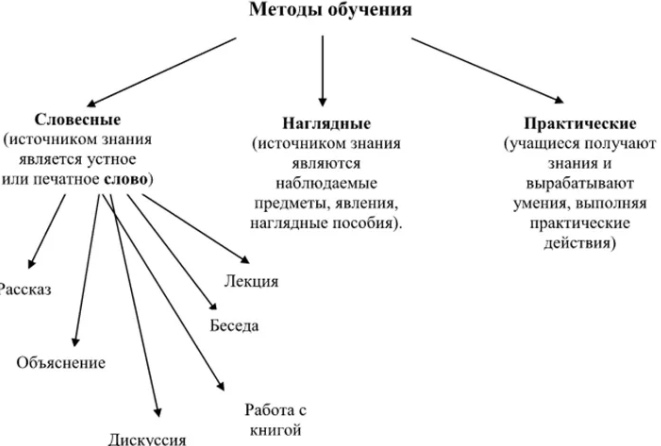
Теоретические основы и технологии начального математического образования

Семиотические аспекты обучения математике в начальной школе

Чтобы стать объектом изучения и применения, математический объект, как идеальный концептуальный образ, конструируемый познающим субъектом в процессе деятельности, «материализуется» в реальном мире знаком — элементом системы знаков. Смысл и значение знака основаны на соглашении (конвенции) между теми, кто его использует. В единстве означающего и означаемого знак участвует в процессе культурной коммуникации и служит, с одной стороны, формой хранения знаний, а с другой — средством приобретения новых знаний. Последовательность знаков, построенная по определенным правилам, образует текст. Тексты, в отличие от одного знака, обладают неограниченными возможностями хранения знаний (информации) и выполнения функции получения новых знаний. Система знаков — семиотическая система — как средство культурной коммуникации представляет собой язык, понимаемый в широком смысле. Это свойство знаковых систем определяет их важность в образовании. Семиотический подход означает использование различных языков в обучении математике для построения концептуальных образов изучаемых объектов.

Ч. Пирс (1839-1914) — один из основателей семиотики (науки о знаках и знаковых системах) выделял три типа знаков: Значки, индексы и символы. Значки обозначают объект, который максимально приближен к обозначаемому объекту. Это могут быть рисунки, предметы, фотографии и т.д. Индексные знаки служат обозначением не самих объектов, содержащихся в рассматриваемой ситуации, а тех их характеристик, которые абстрагируются в процессе поиска, сохраняя частично визуально воспроизводимые отношения к исходной ситуации. Знаки-символы не имеют ничего общего с обозначаемым объектом; они воздействуют на наши органы восприятия не сами по себе, а с помощью информации, которую они несут. В то же время сенсорно-визуальный знак создает точку опоры для мысли, центр, вокруг которого возникают различные ассоциации, не позволяющие мысли погрузиться в поток представлений и идей.

Синтаксис семиотической системы — это формальные правила, определяющие способ построения текстов (предложений, высказываний) с помощью данной системы и способ их преобразования, т.е. синтаксис — это отношения знаков друг к другу.

Отношения знаков к внешнему миру, к объектам, обозначаемым знаками, составляют семантику системы, которая определяет смысловое содержание информации, представленной текстом. Отношения между знаками и теми, кто их использует, — это прагматика системы, она характеризует ценность и полезность сообщаемой информации.

Специальный научный язык математики, без владения которым невозможно познание математики, образует семиотическую систему, обладающую рядом характеристик. Во-первых, его синтаксис — это достаточно «жесткая» система правил, которая однозначно определяет структуру выражений математического языка и способ их функционирования. Во-вторых, в отличие от естественного языка, например, русского, предложения математического языка, как правило, не допускают различных толкований и двусмысленностей, то есть представления математических объектов средствами математического языка однозначно их определяют. В то же время существуют глубокие причины, по которым идея, выраженная исключительно на символическом языке, искусственно созданном математиками, трудна для восприятия; поэтому представление математических объектов не ограничивается языком математических знаков, а обращается как к обычному живому языку, так и к знакам, не являющимся математическими.

Обозначение объекта с помощью определенной семиотической системы является его именем. Имя определяет объект, которому присвоено это имя, а сам объект является значением (денотатом) имени. Один и тот же объект может иметь разные имена. Например, «периметр прямоугольника» и «сумма длин сторон прямоугольника» — это названия одного и того же объекта. Но название «периметр прямоугольника» обозначает лишь то, что объект с таким названием существует, а название «сумма длин сторон прямоугольника» обозначает вполне конкретную геометрическую конструкцию, из чего видно, что их смыслы не совпадают. Это несоответствие легко увидеть, сравнив вопросы: Человек с недостаточными знаниями может вполне обоснованно спросить, является ли периметр прямоугольника суммой длин его сторон, но было бы нелепо спрашивать, является ли периметр прямоугольника периметром прямоугольника.

Понимание математики младшими школьниками

Одна из самых больших проблем для детей — это понимание мира, в котором они живут. Понимание мира включает в себя не только знания о мире, но и понимание объективного мира, отраженного в знаниях, и понимание самого знания. Понимание предопределяет осмысленное поведение, возможность ориентации в социальной жизни, в культуре, в истории. В самом общем виде понимание характеризуется как универсальная когнитивная способность, один из важнейших аспектов развития человеческого мира.

Понимание тесно связано со знанием, но не совпадает с ним. Можно знать и не понимать. Таким образом, чтобы найти сумму 27 + 8, достаточно знать соответствующий прием, и не обязательно понимать, почему нужно действовать именно так. В то же время решение проблемы: «Когда из бочки удалили 8 литров воды, в ней осталось 27 литров. Сколько литров воды было в бочке изначально?» требует не только знания понятий, подразумеваемых в тексте, но и понимания связей и зависимостей между ними. Понимание, с одной стороны, выражает определенное состояние познающего субъекта, а с другой стороны, обусловлено природой и структурой познаваемого объекта.

Познание математики — это сложный процесс формирования концептуальных форм знаний. Факты, явления и теории считаются понятными, если они укладываются в рациональную схему, являющуюся результатом осмысления знаний. Особый онтологический статус математических объектов, идеальных абстракций, создаваемых активной деятельностью сознания в процессе освоения окружающего мира, является объективным фактором, осложняющим понимание математики учащимися. Человеческая тенденция к объективизации идеального заставляет математические абстракции казаться конкретными через представление знаков, придающих форму математической реальности, которую студенты часто отождествляют с объектом, который они пытаются представить.

О необходимости понимания математики и причинах ее непонимания в процессе обучения говорили такие математики, как Ж. Адамар, А. Пуанкаре, А.Н. Колмогоров, В.А. Успенский, В.А. Гусев, В.Г. Дорофеев и другие. Среди причин непонимания были:

Обучение студентов лишь конечный результат творческих усилий математиков, который остается только воспроизвести;
Сложность логической и грамматической структуры текстов, определяющих математические понятия
Отсутствие визуальных представлений изучаемых понятий;
Пренебрежение изучением знаков в ущерб развитию концептуальных навыков.
Неадекватная способность связно рассуждать;
Рациональность и невежество образного обучения.

Ориентация обучения на понимание математики требует выделения таких средств описания, которые способствовали бы созданию условий для формирования в сознании ребенка понятийного образа распознаваемого объекта, соответствующего его объективному содержанию. Такие средства должны обеспечивать полноту представления в концептуальной картине ее структурных когнитивных компонентов. По мнению М.А. Холодной, обязательными когнитивными компонентами ментальной концептуальной картины являются вербально-лингвистический, сенсорно-чувственный, визуально-пространственный, операционально-логический, операционально-символический.

Формирование вербально-лингвистических компонентов будет тем успешнее, чем большим набором выразительных средств располагает педагог. Например, при переформулировании текста приведенной выше задачи понимание быстрее и полнее достигается при использовании здравого смысла, когда говорится, что воды взяли столько же, сколько и оставили. Сенсорный компонент формируется в процессе действий детей с предметами. В этом случае такие действия могут быть действиями переполнения, которые вместе с рисуночным образом проблемной ситуации приводят к формированию визуально-пространственных компонентов образа воображения.

Методика обучения математике в начальной школе: становление и развитие

Одним из самых ранних сохранившихся математических трактатов является папирус Ринд, написанный Ахеменом около 2000 года до н.э. По мнению историков математики, он предназначался для обучения писцов и является копией более древнего источника. Папирус начинается с объяснения техники счета. Техника сложения была очень простой, аддитивный принцип записи чисел сводил сложение к сопоставлению одного ввода с другим. В то время как сложение и вычитание были вполне освоенными операциями, умножение не существовало как особая операция.

Поскольку одной из задач писцов было определение количества людей, необходимых для рытья канавы, количества кирпичей для строительства, площади участка земли, объема зернохранилища и т.д., папирус содержит решения задач прикладного характера. Даны задачи на определение площадей прямоугольников, треугольников, трапеций и кругов и приведены их решения. Высший уровень составляли задачи, решаемые методом ложной позиции: «Множество и его четвертая часть дают в сумме 15». Египетское решение: отсчитайте от 4, отнимите четверть, а именно 1, вместе 5. Затем разделите 15 на 5 и умножьте результат на 4. Искомое число равно 12. Такие задачи не были вызваны практическими потребностями, но, очевидно, были придуманы людьми, которые любили считать, чтобы попрактиковаться в трудном искусстве счета. Никаких общих правил, не говоря уже о теоретических обобщениях, для решения задач не приводилось. Они определяли способы обучения: запоминание, воспроизведение, действие по образцу, что вызывало значительные трудности, несмотря на то, что образование было рассчитано на узкий круг избранных.

Египетский способ умножения сохранялся до эллинистического периода, и в греческих школах его называли «египетским счетом». Даже в Средние века удвоение dupltatio, как и уменьшение meditatio вдвое, рассматривалось как самостоятельный акт. Когда деление не помогало, египтяне прибегали к дробям. Существовал ограниченный выбор дробей, для которых существовали специальные названия: 1/2, 1/3, 2/3, 1/4, 3/4, 1/6, 1/8. Правила счета половинками, третями и шестыми египетский счетчик должен был запомнить.

Античная (греко-римская) и средневековая системы образования основывались на семи гуманитарных искусствах. На низшей ступени школьного образования изучался тривиум: Грамматика, диалектика, риторика. На высшем уровне — квадривиум: арифметика, геометрия, астрономия, музыка. Наиболее важным арифметическим текстом стала книга Никомаха Геразского (I век н.э.) «Введение в арифметику», в которой автор, следуя пифагорейской традиции, ставит главной целью описание чудесных и божественных свойств чисел в доступной форме. Так, в «Арифметике» было изложено учение о совершенных числах, которые равны сумме всех делителей числа, кроме суммы самих делителей. Например, 6 = 1 + 2 + 3 — совершенное число. В настоящее время с помощью компьютера найдено более 30 идеальных чисел.

Пифагор, проповедовавший, что Бог положил числа в основу миропорядка, был одним из тех, кто освободил математику от всех практических приложений. Математика была формой свободного развития для свободного человека, в отличие от образования ремесленника. У свободных эллинов было много времени для занятий наукой и искусством. К середине пятого века до нашей эры софисты, учителя мудрости, пользовались большим уважением. Среди богатых людей считалось обязательным уметь вести философские беседы, поэтому они отдавали своих сыновей в ученые софисты. В центре научной жизни находилась фигура Платона. Платон требовал от всех своих учеников глубокого знания математики. Только математика, говорил Платон, может научиться думать о вещах, которые не видимы и не слышимы, но существуют в идеальном мире и открыты для интеллектуальных усилий человека. У Аристотеля был другой взгляд на природу математики. Согласно Аристотелю, математика создается познающим человеком в процессе деятельности в реальном мире.

Освобождение науки от практических нужд и провозглашение ее главной целью свободного поиска истины позволило греческим ученым сделать качественно новый шаг в понимании окружающего мира, что подняло античную науку на такой высокий уровень, который и сегодня вызывает восхищение и изумление.

Математическое развитие младших школьников

Математическое развитие как процесс с позиции теории психологической деятельности А.Н. Леонтьева можно охарактеризовать как формирование математического образа мира и своего «Я» в этом мире в сознании ребенка в процессе овладения математическим опытом.

В методико-математических и психолого-педагогических исследованиях термины «математическое развитие», «математические способности», «математическое мышление», «математическое образование» часто служат обозначением одного и того же процесса, в котором выделяются разные стороны. Так, А.Н. Колмогоров называет математическими способностями: умение преобразовывать буквенные выражения, или «вычислительные и алгоритмические навыки», «геометрическое воображение» или геометрическую интуицию, искусство последовательного, правильно расчлененного логического мышления. В.А. Крутецкий, обладая наиболее значительными исследованиями математических способностей, подчеркивал, в частности, способность к формализации математического материала, умение абстрагироваться от конкретных количественных отношений и пространственных форм, умение работать с формальными структурами математических отношений и связей. Структура математических способностей, по мнению В.А. Крутецкого, имеет вид:

Приобретение математической информации;
Обработка математической информации;
Хранение математической информации;
общий пластиковый компонент.

Н.Г. Салмина выделяет способность к знаково-символической деятельности как один из необходимых параметров математических способностей.

Подчеркивая необходимость математического развития в общем образовании, академик А.И. Маркушевич подчеркнул, что решение достаточного количества задач и усвоение отдельных фактов математической науки не является гарантией математического развития. Математические сущности, не имеющие эмпирического прототипа в мире вещей, возникают в результате творческой деятельности человеческого сознания и существуют в виде ментальных концептуальных образов. Чтобы стать объектом познания, концептуальный образ репрезентируется знаком (словом, текстом), главное требование — он должен быть понятен другим. Смысл математического объекта не заменяет никакой материальной вещи, которой можно было бы придать смысл.

С этой точки зрения, математическое развитие — это развитие способностей человека создавать концептуальные образы математических объектов и оперировать ими в процессах решения познавательных задач. Логически существует два способа создания концептуальных образов математических объектов в процессе обучения. Первая направляет познание «от знака к смыслу». Суть в том, что смысл формируется в сознании учащихся в процессе работы со знаками по правилам математического языка. В этом случае сами правила являются объектом обучения, а степень овладения ими — одним из показателей математического развития. Знаки дают возможность хранить понятия в «свернутом виде», сокращают непродуктивную мыслительную деятельность, разгружают воображение и память. Оперирование знаками математического языка, в соответствии с его синтаксическими правилами, часто заменяет набор умозаключений и в то же время требует определенной сноровки, которая вырабатывается упражнениями.

На странице курсовые работы по педагогике вы найдете много готовых тем для курсовых по предмету «Педагогика».

Здесь темы рефератов по педагогике

Читайте дополнительные лекции: