Задача №8.
Точка описывает плоскую кривую. Радиальная составляющая скорости точки положительна и постоянна по величине, а радиальная составляющая ускорения отрицательна и обратно пропорциональна кубу расстояния от некоторого полюса. Определить траекторию и секторную скорость точки.
Решение:
Аналитическое решение этой задачи следует непосредственно из определения радиальной и трансверсальной составляющих ускорения материальной точки. Имеем
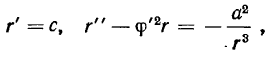
откуда

Разделив второе из последних уравнений на первое, будем иметь

Отсюда получаем конечное уравнение траектории
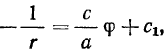
где
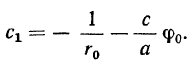
Окончательно можно записать:
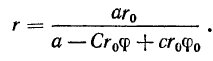
Из формулы
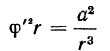
непосредственно получаем

так что секторная скорость точки будет равна
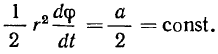
Из-за того, что оси -полярной системы координат являются подвижными, создаются искусственные трудности и при исследовании движения материальной точки, отнесенной к полярным осям.
Задача взята со страницы подробного решения задач по всем темам теоретической механики:
Решение задач по теоретической механике
Возможно эти дополнительные задачи вам будут полезны:
