Оглавление:





Точные решения уравнении ламинарного пограничного слоя для плоской пластины
- Создание ламинарного пограничного слоя вдоль плоской бета-пластины при постоянном давлении для стационарных условий изучалось достаточно быстро путем интегрирования уравнений течения пограничного слоя. Эти расчеты основаны на l. -x, показав, что Прандтль может преобразовать дифференциальные уравнения в частных производных (6-16) и (6-18) в полные дифференциальные уравнения для условия течения при consideration. It исполнял Блазиус.
2 дифференциальные уравнения, описывающие поток, можно объединить в 1 уравнение, введя функцию потока, определяемую следующим образом. df. ч = — т -; в = — 3 -. Сделайте dh. Введение функции тока в уравнение неразрывности (6-18) удовлетворяет этому уравнению. Уравнение импульса (6-16) принимает вид: dfd2fdfd2f_ Д » Ф дю dhdu2du⁹ dhdu ’ (6-43) Л. Прандтль показал, что это уравнение можно преобразовать в обыкновенное дифференциальное уравнение, введя новую независимую переменную И предположим, что текущая функция может быть записана следующим образом: Где f-только 1 функция.
Для изменения внутренней энергии системы посредством теплообмена также необходимо совершить работу. Людмила Фирмаль
Введение в эти 2 новых Параметры f и q уравнения импульса дают новое уравнение. ^ + ^ = ° — (6-44) Граничное условие (6-19) для 2 новых переменных: для m] = 0 По Т| — ОО £= 2 Понятно, что функция f сразу описывает 2 составляющие скорости в соответствии с соотношением. Блазиус решил это уравнение, последовательно разложив функцию f. После того, как Пирси и Престон [l. a. 54]показали другой способ привести к более простому решению путем последовательного approximation. To для этого 2-я производная от f обозначается через r.
Дифференциальное уравнение принимает вид: Если в какой-то момент Вы думаете о f как о заданной функции tj, вы можете разделить переменные. Интегрировать lnz = — j’f ^ + lnci; z = c₁e’if4 При дополнительной консолидации получается следующая формула для скорости и пограничного слоя: в utj-j-cj. Константы cj и С₂ определяются из граничных условий, и после подстановки может быть получена следующая формула. °ДФ Йе} О И затем О (645) Поскольку функция f, появляющаяся в экспоненте справа от уравнения, неизвестна, то это уравнение нельзя рассматривать как решение уравнения (6-44). Однако он может быть использован для получения решения путем последовательного приближения следующим образом: Производится первая оценка функции f.
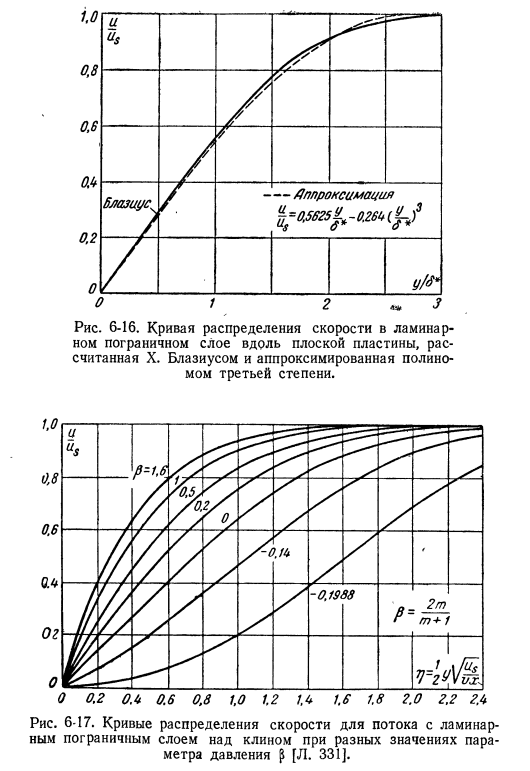
- Это значение подставляется в уравнение (6-45), и уравнение решается относительно и. Дополнительные интегралы дают f, которые также могут быть заменены в уравнение (6-45) в качестве 2-го приближения функции f. Интегрирование дает 3-е соответствие, поэтому вы можете продолжать до тех пор, пока последовательные приближения не будут хорошо согласованы. Ppersy и Престон начали расчет из грубого предположения, что/ = 2m]и получили очень хорошее решение для профиля скорости с 3 последовательными повторениями. Профиль скорости, полученный таким образом, показан на рисунке. 6-16.
Здесь же показаны профили, описываемые формулой (6-26), с одинаковой толщиной пограничного слоя. Эта диаграмма показывает, что матч очень удовлетворительный. Точное решение уравнения ламинарного пограничного слоя также может быть получено для двумерного течения на поверхности, если скорость течения изменяется в соответствии с соотношением. И затем Это распределение скоростей установлено вдоль поверхности бесконечного клина с углом раскрытия a = 2tl / (t + 1) = pl, с несжимаемым потоком, ориентированным симметрично к вершинам. Поэтому эти растворы относятся к типу потока раствора для промывки клина.
Однако это не механическая работа, которая связана с перемещением границы макроскопической системы. Людмила Фирмаль
Опять же, преобразование уравнения границы Рисунок 6-16. X. Кривая распределения скорости ламинарного пограничного слоя вдоль плоской пластины, вычисленная по Блазиусу и аппроксимированная полиномом 3-го порядка. Рисунок 6-17. Параметры давления£[l. Кривая распределения скорости потока с ламинарным пограничным слоем на вершине клина для различных значений. 331]. Те же преобразования, которые использовались ранее, могут быть стратифицированы в обыкновенные дифференциальные уравнения.
Конечным дифференциальным уравнением совершенной производной является[l. 55. : ^₊ф* т ___ ^ _rm2_ii ₌ ₀ ФПИ. Дж. (6-46) Профиль скорости этого типа потока показан на рисунке. 6-17. Профиль для параметра p = 0 (/l = 0) является профилем Блазиуса. Положительное значение p или t указывает на увеличение скорости вдоль поверхности. Величина m — (p = 1) соответствует углу клина a = 180 *или 2-мерному потоку, обычно направленному на плоскую пластину.
Этот поток также возникает вблизи шины тупого цилиндра. Отрицательное значение m соответствует потоку, скорость которого уменьшается вдоль поверхности. Значение m = −0. 1104 (p = −0. 1988) характеризуется тем, что градиент скорости этого профиля вблизи поверхности равен нулю (профиль отрыва потока).
Смотрите также:
| Движение вдоль плоской стенки | Движение жидкости в трубе |
| Градиенты давления вдоль поверхности | Поперечное обтекание цилиндра |
