Оглавление:







Влияние гироскопических сил на свободные колебания твердого тела
- Чтобы составить дифференциальное уравнение малых колебаний твердых тел при наличии гироскопической силы, необходимо применить теорему о движении центра инерции системы материальных точек, а также теорему об изменении основного момента импульса системы материальных точек в относительном движении относительно центра инерции. Согласно первой теореме Эл С Р, МПЦ с-а. Где M-масса твердого тела, xc, Vc rc-координата центра инерции силы тяжести твердого тела в системе неподвижных координатных осей, RJ, K , R — проекция главного вектора внешней силы, приложенной к твердому телу. Вторая теорема приводит к соотношению СЖО, dLcv Ви Ви Ви -гг 2 ТС-ый 2.
Где Lcx, Lcv и Lq-главные моменты импульса для оси, поступательно движущейся вместе с центром инерции гравитации твердого тела, а Y , m F — главные моменты внешних сил на той же оси. Когда осесимметричное твердое тело вращается вокруг оси симметрии с большой угловой скоростью 0, это совпадает с отсутствием колебаний оси x и малого объекта, и является главным моментом импульса к координатной оси перемещения, вплоть до 1-го измерения, центра инерции твердого тела.
Как известно, переносное поступательное движение системы происходит как движение абсолютное под действием всех внешних сил системы и сил инерции масс в их относи-тельном движении, т. Людмила Фирмаль
Где D-твердый момент инерции относительно оси симметрии, B-перпендикулярно оси симметрии и B-твердый момент инерции относительно любой оси через центр инерции тела, p-малое вращение оси симметрии, измеренное от оси x плоскости xy, и P-малое вращение оси симметрии, измеренное от оси XY плоскости. При исследовании поперечных колебаний малые продольные перемещения твердых тел обычно игнорируются. То есть предположим, что координата xc не изменяется. Тогда первое уравнение 1 disappears. In кроме того, при учете равномерного вращения твердого тела первое уравнение системы 2 также исчезает.
Для решения задачи о свободной вибрации твердых тел, которую можно предположить выше, мы рекомендуем следующую процедуру. 1 Выберите 2 системы координат. Первая система фиксируется на твердом теле, а вторая-на неподвижной системе координат. 2 применить теорему к движению центра инерции, чтобы создать 2 дифференциальных уравнения для движения центра тяжести. 3 используя теорему об изменении главного момента импульса в относительном движении относительно оси, движущейся постепенно вместе с центром инерции, построим оставшиеся 2 дифференциальных уравнения малых колебаний твердых тел.
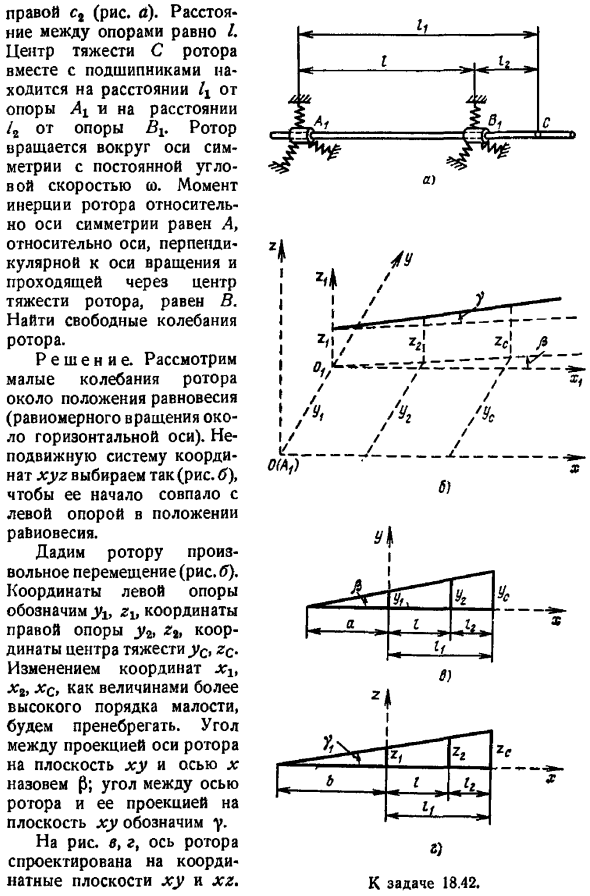
Результаты дифференциального уравнения движения твердого тела интегрируются с системой и находят частоту свободных колебаний, основную вибрацию ротора и общее решение задачи. Задача 18.42.Жесткий ротор с массой M вращается с 2 упругими опорами L1 и Rj. Коэффициент жесткости левой опоры Справа с рисунок а. Расстояние между опорами равно I. центр тяжести Ротора C расположен на расстоянии Zj от опоры At, вместе с подшипником, и на расстоянии Z2 от опоры Bi. Ротор вращается вокруг оси симметрии с постоянной угловой скоростью. Момент инерции ротора относительно оси симметрии равен А и равен в, перпендикулярен оси вращения, относительно оси, проходящей через центр тяжести Ротора.
Найдите свободную вибрацию Ротора. Решение. Рассмотрим малую вибрацию Ротора вблизи положения равновесия равномерное вращение вокруг горизонтальной оси. Выберите положение системы координат, которое не может быть перемещено рисунок Y .так, чтобы его начальное положение совпадало с левой опорой в положении равновесия. Дайте Ротору любое движение рисунок B .Левые координаты опоры обозначаются буквой Z , правые координаты опоры-y, z, усы-координатами центра тяжести, zc. Изменение координаты xlt xt игнорируется как меньшее значение степени. угол между проекцией оси ротора и осью x в плоскости xy называется p. угол между осью ротора и проекцией на плоскость x y обозначается y.
Фигуры c, d и оси ротора выполнены на координатных плоскостях xy и xz. х Z х 0 а б Я 2 д К выпуску 18.42. Представляет координаты и углы центроида 5, через независимые координаты yt, которые определяют положение идеально Ротор. B, c, d, исходя из рисунка Дж С Л-Г Л О КЦ — Зи — З — -, 2 В 3 Б 4 Основываясь на теореме о движении центра инерции, можно написать 2 дифференциальных уравнения L1rs — c1 1-ca 5 Л с — Ви-с, 6 С правой стороны имеется выступ на соответствующей оси упругой реактивной силы пружины. приступим к построению дифференциального уравнения малых колебаний ротора вокруг осей, параллельных y и r, проходящих через центр инерции колебательной системы.
Основной момент импульса системы включает в себя десятичные дроби первого порядка с небольшим количеством максимум L, 4, 7 8 часов вечера. З. 4 ой Б. 9 Основные моменты внешней силы относительно нарисованной оси. Через центр инерции, рисунок а 10 2 tSu F — ZtCtlt-ZicJi, 11 2 С2 Ф ytcilt y1c1ll.
- Используя теорему и формулу 8 — 12 об изменении основного момента импульса при относительном движении относительно центра инерции у. Зи Зі, 13 Эш Б УЗК у. 14 Уравнение 5 6 13 14 получаем значения yy, Zq, P T , YV Yy zlt z, находим систему из 4 линейных однородных дифференциальных уравнений л Аль-ш ctiyt о М,- А ctlzt 0 Ла П-Х −5 2х-2х С4, ЗЗ, 0 L u x, −2 B J a-A —fivj i . Конкретное решение для этой системы требуется в виде Ух Д грех р а ух да грех пз КТ ЗТ ДТ Кос р а З2 D4cos р а ДП Д, Здесь. Da, 4, p, -постоянная 19 делится для удовлетворения системы дифференциальных уравнений 15 — 18.
Вводя 19 в 15 — 18, сокращение каждого из них на sin pZ a и cos pt a , и сокращение таких членов, Z Однородная система из 4 алгебраических уравнений относительно I, Dt, D3, Dj. кросслинкинг- мл МДж ДТ м, ЦЗ A4Z8p2 Д8 С, З-М 1П Д4.Ноль -А mpDx AmpDt с з-ВР Д3 c2Z2Z ВР ДТ 0,я ВР — СХ л Ди- ВР CjZ, З Д AmpDa — AmpDa 0.Дж Легко показать, что система 20 делится на 2 parts. In факт, если вы сложите и вычитаете первые 2 уравнения и последние 2 уравнения, вы получите C1Z Ml Dx D, c, Z-Mlxp Da Dt 0 cxZ Ml Dx-D. 4- ctl-MlxP Dt-DJ 0 ВР пож-CxV ДХ да — ВР Лcop с, Z2Z ДТ ди-джей 0 ВР — пож-qZxZ ДХ-Оз — ВР — амп cttl да-ДТ 0.
В условиях отсутствия болтов механизм может начать подпрыгивать над горизонтальной плоскостью. Людмила Фирмаль
Когда группа уравнений получается система найти на ZX и ДТ ДТ cxl Mlxp Dx Dg 4- c, Z-Mlxp Dt D. 0, x ВР Пож-Cxlxl ДХ ДС — Я 21 — ВР усилок 4-КШЗ, з ДТ ди-джей 0 Дж. Система для поиска и ох-Д и ДТ-ДТ cx1 м СП ДТ-Д3 с Л- Ди-Ди 0, БПИ-На-CiliD Д1-Д3 — 22 — Брг-топ ДТ-Д4 0. Если уравнять детерминанты системы 21 и 22 до нуля, то получим 2 частотных уравнения Б СР-эрф-qZJ м с — Алп qZx КЗ, 0 23 Bp2-Atop-erf-qZJ fa с, — Alp erf qZj 0. 24 Докажем, что в уравнениях 23 и 24 нет общих корней. Предположим, что существует общий корень pt. Тогда в случае p pi оба уравнения удовлетворяются одновременно. Если вычесть 2-е выражение из первого выражения 2лшд1 CJ Q-ALPF 0 То есть общий корень — ЗЕ.
Однако оба эти значения не соответствуют исходному уравнению. Здесь мы покажем, что корни уравнения частоты являются real. To сделайте это, рассмотрим функцию Л Р ВР поверх-КЗ — КЗ М м-АФП qZx эрф 25 Л Р Вр2-на-Фэр-Фэр, м м-Алп qZx crfp. 26 и найти значение некоторых характерных значений аргумента p. — ае-Со-Оо — са са бесплатный Wi кя 0-qql 4 З С а г 1 ДУ — Утвердительный ответ. По существу, описанная операция подразумевает разложение коэффициентов частотного уравнения системы 20.
Из таблицы видно, что если аргумент p изменяется с-oo на oo, то непрерывные функции A p и, p меняют знак 4 раза. Напомним, что 23 и 24 являются уравнениями 4-го порядка, можно утверждать, что каждое из уравнений 23 и 24 имеет 2 отрицательных и 2 положительных корня, то есть корни обоих уравнений являются real. It следует отметить, что рассматриваемый корень обладает интересными свойствами. Отрицательный корень 1 уравнения имеет абсолютное значение, равное положительному корню другого уравнения, и наоборот. При угловой скорости, равной нулю, уравнения 23 и 24 совпадают и принимают вид ВР — компакт-диска-CD н с — Мп С111 ЦТЛ 0. 27 7.
Корень формулы 27 определяет частоту свободных колебаний невращающегося Ротора. На рисунке e показан график функций f P A P и f P кроме того, f0 p показывает левую часть 27. Как видно из графика, положительные корни этих уравнений, то есть частоты свободных колебаний Ротора, расположены в следующем порядке Pr Po Pi Pi Po Pt — 28, где pi-частота свободных колебаний невращающегося Ротора.
Из формул 21 и 22 видно, что для корней первого частотного уравнения конкретное решение будет иметь вид У1 Г грех ПФ Т ЗТ Ди Кос ПТ а д Я D1sin ПФ а Р ДТ со пи а В этом случае система 22 имеет только тривиальное решение D1-Da 0 и—D4 0, поэтому для корня 2-го частотного уравнения оно выглядит так 1 D1sin ПФ а, — Djcosfpi а, я ya Д, Син п а, я 1 з — да со п а. Дж Нетрудно убедиться, что приведенные выше особенности уравнения корневой частоты позволяют ограничиться 29 и 30 заменой только положительного корня соответствующего частотного уравнения. Это связано с тем, что отрицательный маршрут не приводит к новому линейному независимому частотному решению.
В результате 1-я и 2-я ключевые вибрации соответствуют корням pr и p .Где ось ротора представляет собой конус, который вращается в том же направлении, что и Ротор. Эти движения называются прямой прецессией Ротора. В прямой прецессии вектор угловой скорости твердого тела при вращении вокруг оси симметрии и вектор угловой скорости оси ротора образуют острый угол. корни pr и p1 соответствуют 3-му и 4-му основным колебаниям, когда ось ротора рисует конус, который вращается в противоположном направлении от вращения ротора. Эти движения называются обратной прецессией ротатора.
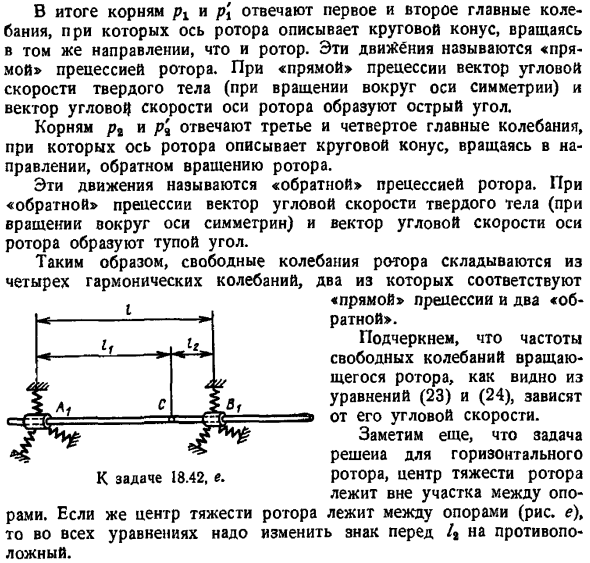
В случае обратной прецессии вектор угловой скорости твердого тела при вращении вокруг оси симметрии и вектор угловой скорости оси ротора образуют тупой угол. Итак, свободная вибрация Ротора состоит из 4 гармонических колебаний, 2 из которых соответствуют прямой прецессии, а 2 из которых соответствуют обратному движению. Как видно из формул 23 и 24, подчеркнем, что частота свободных колебаний вращающегося ротора зависит от его угловой скорости. Также отметим, что горизонтальная задача решена Выпуск 18.42, e. центр тяжести Ротора Он находится за пределами области между опорами. Если центр тяжести Ротора находится между опорами рис.
Смотрите также:
Предмет теоретическая механика
