Оглавление:

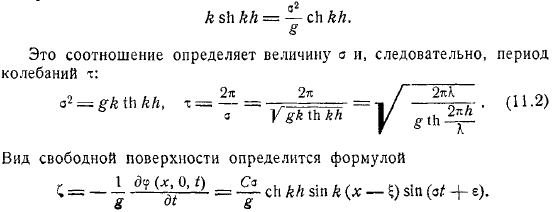

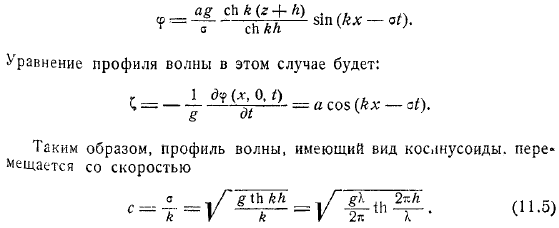





Волны при конечной глубине жидкости
Теперь предположим, что глубина жидкости конечна и равна. Ограничимся выводом формулы для стоячих и бегущих волн в этом случае. Опять же, существует уравнение, которое предполагает, что дно жидкости горизонтально и что уравнение действует как фиксированное.
Уравнение гидродинамики выглядит следующим образом: если эти продукты не соответствуют вашим потребностям, пожалуйста, свяжитесь с нами, и мы хотели бы предоставить соответствующую информацию. Итак, в этом случае существует стоячая волна, а потенциал скорости равен. Остается удовлетворить уравнению, которое дает отношение.
- Это соотношение волны определяет величину, а значит и период колебаний. Тип свободной поверхности определяется по формуле. Я введу обозначения.
- Тогда мы получаем следующую формулу для потенциала скорости и профиля волны (предполагая для простоты).
Людмила Фирмаль
Поскольку проекция скорости частицы на координатные оси определяется формулой, уравнение движения любой частицы выглядит следующим образом после интегрирования оно заменяется формулой. Далее рассмотрим, например, бегущую волну, движущуюся в направлении положительной оси. То есть рассмотрим упражнение с потенциалом скорости.
Уравнение профиля волны в этом случае выглядит следующим образом. Поэтому профиль волны в виде косинусной волны движется со скоростью. Интересно отметить на поверхности раздела двух жидкостей и граничных случая. Если глубина жидкости очень большая (или соотношение очень большое).
- Потому что вы можете взять равный. То есть, вы получите знакомую формулу. Другой ограничительный случай-когда глубина очень мала (или если соотношение мало).
- В этом случае это означает следующее. То есть для малой глубины жидкости скорость распространения волн не зависит от их длины.
Он предоставляет таблицу, которая может рассчитать скорость распространения волны различной длины. Эта пластина была рассчитана с использованием выражения. Найти орбиту частицы в случае бегущей волны. У нас есть. Следовательно. Найти уравнение орбиты частицы, за исключением времени.
Другими словами, путь частицы представляет собой полуосевой эллипс. Людмила Фирмаль
При перемещении она происходит только в горизонтальном направлении, поскольку малая ось поворачивается к нулю, а эллипс входит в отрезок прямой, который расположен ниже. Вращение частицы вдоль эллипса происходит относительно волн, которые распространяются по часовой стрелке, в положительном направлении оси.
Интересно рассмотреть задачу о групповой скорости в случае жидкости конечной глубины. Групповая скорость всегда определяется по формуле. В этом деле выражения с равными ограничениями всегда уменьшаются по мере их стремится к нулю при.
Групповая скорость всегда больше половины скорости распространения отдельных волн, и эта скорость меньше, чем. Крайний случай очень малой глубины жидкости, можно сказать, и получается, что групповая скорость совпадает со скоростью распространения отдельных волн. Это и понятно.
Потому что в рассматриваемом случае скорость последнего не зависит от длины волны. Это указывает на особую простоту в случае малой глубины. Мы подробно рассмотрим это в разделах, посвященных длинным волнам и цунами.
