Оглавление:



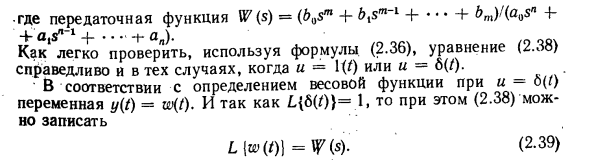

Временные характеристики
- Временные характеристики Другой важной характеристикой автоматических систем (связей) являются переходные и импульсные переходные функции и их графики (временные характеристики). Они используются для описания как стационарных, так и нестационарных линейных систем. Функция перехода системы (связи) — это функция, которая описывает изменение выходного значения системы (связи), когда к входу применяется одношаговое действие, когда начальное состояние равно нулю. Функция перехода обычно представляется как h (t).
Аналитически, эффекты одного шага могут быть объяснены одной функцией График функции перехода, зависящей от времени кривой, функции h (t) называется характеристикой перехода или ускорения. Системная (звенная) переходная или взвешенная переходная функция (весовая функция) — это функция, которая описывает реакцию системы (? Вены) на одно импульсное воздействие при нулевых начальных условиях. Эта функция обозначена как w (t).
В противном случае, функция перехода h (t) является функцией, которая описывает реакцию системы (ссылка) на одношаговое действие при начальном условии, равном нулю. Людмила Фирмаль
График импульсных переходных функций называется импульсным переходным откликом. Переходные и импульсные переходные процессы называются временными характеристиками biMu. При определении весовой функции использовалась концепция единичного импульса. Физически, один импульс может быть представлен как очень узкий импульс, ограничивающий единицу площади. Математически это описывается функцией b (/), называемой дельта-функцией. Дельта-функция является обобщенной функцией.
Теория обобщенных функций является относительно новым разделом функционального анализа и здесь не рассматривается. Обратите внимание, что в рамках теории обобщенных функций функции, встречающиеся в приложении, имеют производные произвольного порядка. В частности, существует производная от единичной функции — такая же, как дельта-функция 1 (/) = & (t). Сама дельта-функция имеет производные в любом порядке. Давайте перейдем к определению дельта-функции и ее производных.
Предмет теория автоматического управления тау
| Формы записи линейных дифференциальных уравнений. Передаточные функции | Элементарные звенья и их характеристики |
| Частотные характеристики | Понятие устойчивости |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- В то же время при решении практических задач, как правило, мы пользуемся тем, что дельта-функция и ее производные могут быть найдены только на промежуточных этапах. В конечном результате они либо полностью отсутствуют, либо появляются под неотъемлемым символом произведения с некоторой «нормальной» функциональностью. Таким образом, вам не нужно отвечать на вопрос о том, что непосредственно представляет собой дельта-функция, но что означает произведение дельта-функции или некоторый интеграл от ее производной?
Исходя из вышеизложенного, дельта-функция может быть определена как: Дельта-функция — это функция со следующими свойствами: f 5 (/) <* / = j $ (/) d / = l, (2,32) — так -r [Α (/) φ (/) Λ = | * (/) Φ (0 dt = q> (0). (2.33) — и — Производная дельта-функции может быть определена соотношением 15 (/) Ф (/) Л = 15 (/) Ф (/) Л = -Ф (0), (2,34) — так -e (M)! (Т) (т) J 5 (/) φ (/) = j 6 (/) ф (/) Л = (_ \ r 9 ‘0), (2,35) -Да- * Где е — любое положительное число. f (/) — функция Оливы. (Вт) 6 (/), которая имеет шестую производную, является третьей производной по времени дельта-функции.
Вода и нормальная функция. Людмила Фирмаль
Найти изображение Лапласа дельта-функции и ее производных. В этом случае преобразование Лапласа рассматривается как предельное соотношение 00 Используйте соотношение (2.32) — (2.35), чтобы легко понять L (6 (/)} = 1, L {5 (/)} = s, …, L {7 (/)} = S «. (2.30) Рассмотрим линейные дифференциальные уравнения с постоянными коэффициентами в общем виде • «KPn +» Y’1 + ••• + ajy = (b0m + + ••• + bm) u. (2.37) На изображении Лапласа это уравнение , Y (секунды) = W (секунды) U (секунды), (2,38)
Где передаточная функция W (s) = (bas «+ b, s-1 + •• + bm) Быстрый способ проверки с помощью Форсюльха (2.36). Уравнение (2.38) также справедливо, когда u = 1 (f) или u. Переменная Следовательно, передаточная функция равна изображению Лапласа весовой функции, поэтому w (t) = L ~ l (W (s) |. (2,40) Вы можете использовать последнюю формулу для расчета весовой функции. Установите связь между весовой функцией и функцией перехода. Поскольку !! (/)} — 1 / s, уравнение (2.38) для u = 1 (/) принимает следующий вид: L \ h (t) \ = W (s) -i. $ Сравнивая эту формулу с (2.39), легко увидеть, что sL (A (/)) = L | a> (0).
Если начальное условие равно нулю, умножение изображения на s соответствует исходной производной и производной от последнего уравнения, w (t) = h (t). «» Весовая функция и переходная функция, как и в передаточной функции, являются исчерпывающей характеристикой системы (звена), когда начальное состояние равно нулю, и могут быть использованы для однозначного определения выходной величины любого входного действия. Свойство преобразования Лапласа 5), I. x (t) = jw (t-T) u (x) dx = jw (x) u (t-x) dx Эта формула действительна только тогда, когда начальное условие равно нулю, аналогично формуле (2.38).
