Оглавление:
Вычисление поверхностного интеграла II рода
Вычисление поверхностного интеграла II рода сводится к вычислению двойного интеграла.
Пусть функция 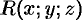 непрерывна во всех точках поверхности
непрерывна во всех точках поверхности  , заданной уравнением
, заданной уравнением 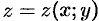 , где
, где 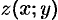 — непрерывная функция в замкнутой области
— непрерывная функция в замкнутой области  (или
(или 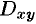 ) — проекции поверхности
) — проекции поверхности  на плоскость
на плоскость 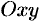 .
.
Выберем ту сторону поверхности  , где нормаль к ней образует с осью
, где нормаль к ней образует с осью 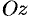 острый угол. Тогда
острый угол. Тогда 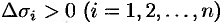 .
.
Так как 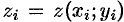 , то интегральная сумма (58.1) может быть записана в виде
, то интегральная сумма (58.1) может быть записана в виде
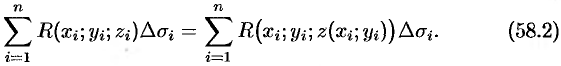
Правая часть этого равенства есть интегральная сумма для функции 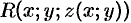 , непрерывной в области
, непрерывной в области  . Переходя к пределу в равенстве (58.2) при
. Переходя к пределу в равенстве (58.2) при 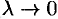 , получаем формулу
, получаем формулу
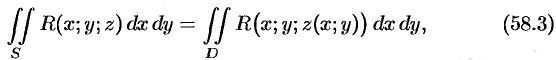
выражающую поверхностный интеграл II рода по переменным  и
и  через двойной интеграл. Если выбрать вторую сторону, т. е. нижнюю, поверхности
через двойной интеграл. Если выбрать вторую сторону, т. е. нижнюю, поверхности  , то полученный двойной интеграл берут со знаком «минус». Поэтому
, то полученный двойной интеграл берут со знаком «минус». Поэтому
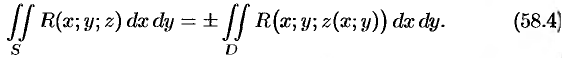
Аналогично
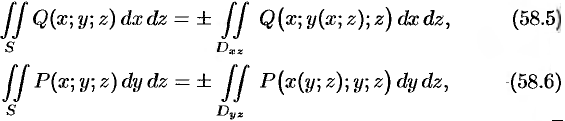
где 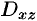 и
и 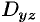 — проекции поверхности
— проекции поверхности  на плоскости
на плоскости 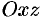 и
и 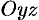 соответственно (замкнутые области).
соответственно (замкнутые области).
В формуле (58.5) поверхность  задана уравнением
задана уравнением 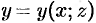 , в формуле (58.6) — уравнением
, в формуле (58.6) — уравнением 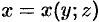 . Знаки, перед интегралами выбираются в зависимости от ориентации поверхности
. Знаки, перед интегралами выбираются в зависимости от ориентации поверхности  (так, в формуле (58.5) берем знак «плюс», если нормаль к поверхности образует с осью
(так, в формуле (58.5) берем знак «плюс», если нормаль к поверхности образует с осью  острый угол, а знак «минус» — если тупой угол).
острый угол, а знак «минус» — если тупой угол).
Для вычисления общего поверхностного интеграла II рода используют формулы (58.4) — (58.6), проектируя поверхность  на все три координатные плоскости:
на все три координатные плоскости:
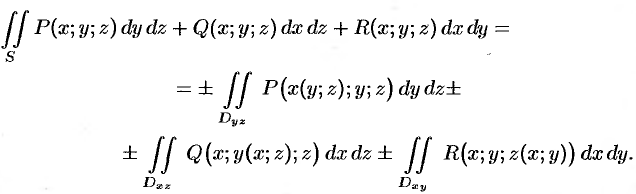
Замечание. Можно показать справедливость равенств
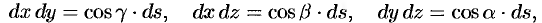
где 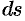 — элемент площади поверхности
— элемент площади поверхности  ;
; 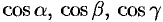 — направляющие косинусы нормали
— направляющие косинусы нормали 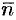 к выбранной стороне поверхности
к выбранной стороне поверхности  .
.
Поверхностные интегралы I и II рода связаны соотношением
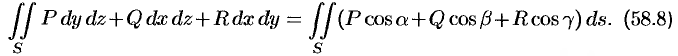
Пример №58.1.
Вычислить
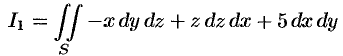
по верхней стороне части плоскости 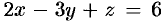 , лежащей в IV октанте.
, лежащей в IV октанте.
Решение:
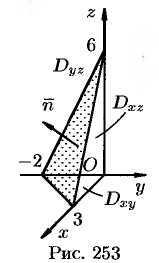
На рисунке 253 изображена заданная часть плоскости. Нормаль 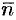 , соответствующая указанной стороне поверхности, образует с осью
, соответствующая указанной стороне поверхности, образует с осью 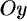 тупой угол, а с осями
тупой угол, а с осями  и
и 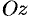 — острые. В этом можно убедиться, найдя направляющие косинусы нормального вектора
— острые. В этом можно убедиться, найдя направляющие косинусы нормального вектора 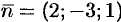 плоскости:
плоскости:
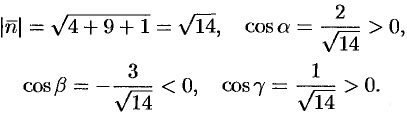
Поэтому перед двойными интегралами в формулах (58.4) и (58.6) следует брать знак «плюс», а в формуле (58.5) — знак «минус». Следовательно,
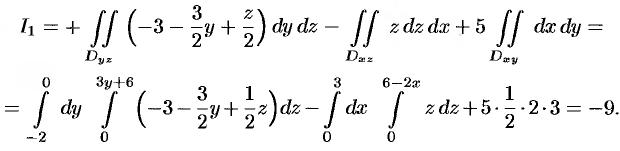
Формула Остроградского-Гаусса
Связь между поверхностным интегралом II рода по замкнутой поверхности и тройным интегралом по объему, ограниченному этой поверхностью устанавливает следующая теорема.
Теорема 58.1. Если функции 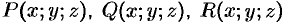 непрерывны вместе со своими частными производными первого порядка в пространственной области
непрерывны вместе со своими частными производными первого порядка в пространственной области  , то имеет место формула
, то имеет место формула
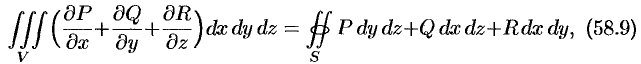
где  — граница области
— граница области  и интегрирование по
и интегрирование по  производится по ее внешней стороне.
производится по ее внешней стороне.
Формула (58.9) называется формулой Остроградского-Гаусса (является аналогом формулы Остроградского-Грина (см. п. 56.3).
Пусть область  ограничена снизу поверхностью
ограничена снизу поверхностью 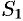 , уравнение которой
, уравнение которой 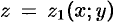 ; сверху — поверхностью
; сверху — поверхностью 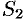 , уравнение которой
, уравнение которой 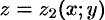 (функции
(функции 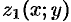 и
и 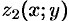 непрерывны в замкнутой области
непрерывны в замкнутой области  — проекции
— проекции  на плоскость
на плоскость 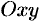 ,
, 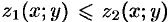 ); сбоку — цилиндрической поверхностью
); сбоку — цилиндрической поверхностью 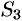 , образующие которой параллельны оси
, образующие которой параллельны оси 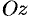 (см. рис. 254).
(см. рис. 254).
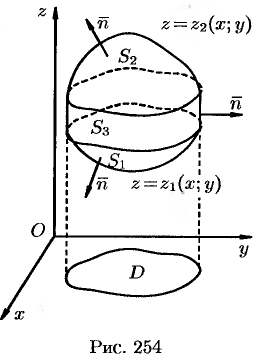
Рассмотрим тройной интеграл
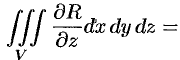
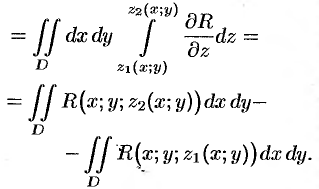
Двойные интегралы в правой части равенства заменим поверхностными интегралами II рода по внешней стороне поверхностей 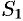 и
и 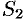 соответственно (см. (58.3)). Получаем:
соответственно (см. (58.3)). Получаем:
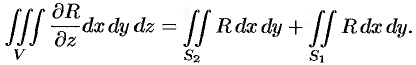
Добавляя равный нулю интеграл 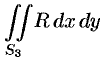 по внешней стороне
по внешней стороне 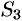 (см. свойство 5 п. 58.1), получим:
(см. свойство 5 п. 58.1), получим:
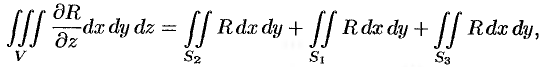
или
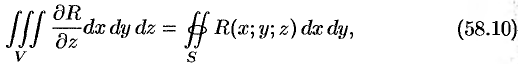
где  — поверхность, ограничивающая область
— поверхность, ограничивающая область  .
.
Аналогично доказываются формулы
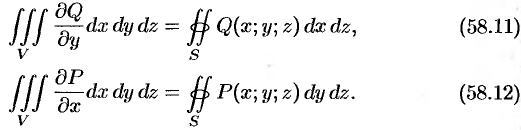
Складывая почленно равенства (58.10), (58.11) и (58.12), получаем формулу (58.9) Остроградского- Гаусса.
Замечания.
- Формула (58.9) остается справедливой для любой области
 , которую можно разбить на конечное число областей рассмотренного вида.
, которую можно разбить на конечное число областей рассмотренного вида. - Формулу Остроградского-Гаусса можно использовать для вычисления поверхностных интегралов II рода по замкнутым поверхностям.
Пример №58.2.
Вычислить 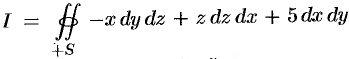 , где
, где  — внешняя сторона пирамиды, ограниченной плоскостями
— внешняя сторона пирамиды, ограниченной плоскостями 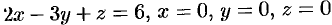 .
.
Решение:
Но формуле (58.9) находим:
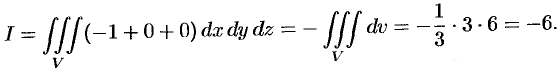
Заметим, что интеграл 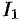 (см. пример 58.1) можно вычислить иначе:
(см. пример 58.1) можно вычислить иначе:
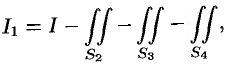
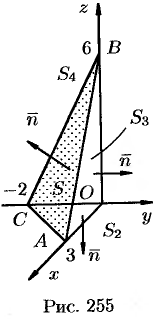
где поверхности 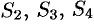 есть соответственно треугольники
есть соответственно треугольники 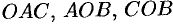 (см. рис. 255).
(см. рис. 255).
Имеем:
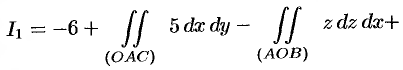
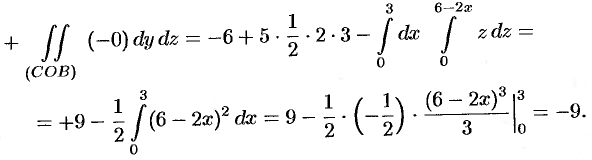
Формула Стокса
Связь между поверхностными и криволинейными интегралами II рода устанавливает следующая теорема.
Теорема 58.2. Если функции 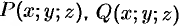 и
и 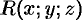 непрерывны вместе со своими частными производными первого порядка в точках ориентированной поверхности
непрерывны вместе со своими частными производными первого порядка в точках ориентированной поверхности  , то имеет место формула
, то имеет место формула
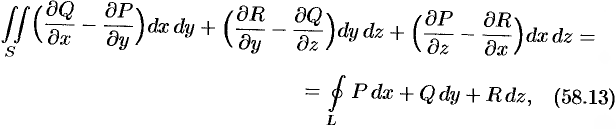
где  — граница поверхности
— граница поверхности  и интегрирование вдоль кривой
и интегрирование вдоль кривой  производится в положительном направлении (т. е. при обходе границы
производится в положительном направлении (т. е. при обходе границы  поверхность
поверхность  должна оставаться все время слева).
должна оставаться все время слева).
Формула (58.13) называется формулой Стокса (Д. Г. Стокс — английский математик, физик).
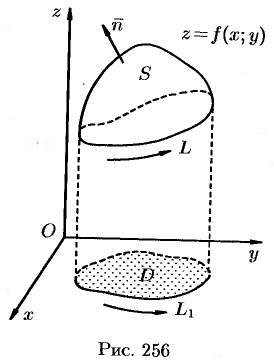
Пусть 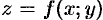 — уравнение поверхности
— уравнение поверхности  , функции
, функции 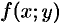 ,
, 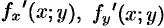 непрерывны в замкнутой области
непрерывны в замкнутой области  (проекции поверхности
(проекции поверхности  на плоскость
на плоскость 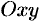 ),
), 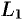 — граница области
— граница области  (см. рис. 256). Будем считать, что поверхность
(см. рис. 256). Будем считать, что поверхность  пересекается с любой прямой, параллельной оси
пересекается с любой прямой, параллельной оси 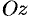 , не более чем в одной точке. Выберем верхнюю сторону поверхности
, не более чем в одной точке. Выберем верхнюю сторону поверхности  . Рассмотрим сначала интеграл вида
. Рассмотрим сначала интеграл вида 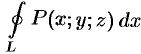 .
.
Значения функции 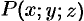 на
на  равны значениям функции
равны значениям функции 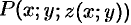 на
на 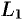 . Интегральные суммы для криволинейных интегралов II рода по контурам
. Интегральные суммы для криволинейных интегралов II рода по контурам  и
и 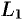 совпадают. Поэтому
совпадают. Поэтому
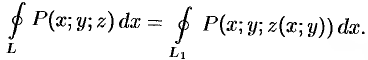
Применим к этому интегралу формулу Остроградского-Грина (см. п. 56.3). Тогда получим:
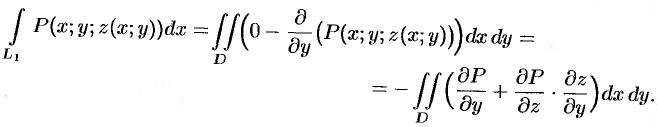
Преобразуем полученный двойной интеграл в равный ему поверхностный интеграл II рода (см. и. 58.2). Для этого последнее равенство перепишем в виде
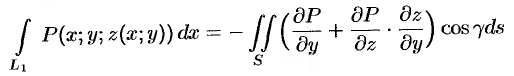
(см. 58.7) и используем уравнение нормали к поверхности  (см. (45.3)). Так как выбрана верхняя сторона поверхности
(см. (45.3)). Так как выбрана верхняя сторона поверхности  , т. е.
, т. е. 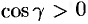 (
(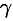 — острый угол между нормалью
— острый угол между нормалью 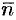 к поверхности
к поверхности  и осью
и осью 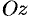 ), то нормаль
), то нормаль 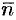 и имеет проекции
и имеет проекции 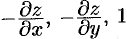 . Направляющие косинусы пропорциональны соответствующим проекциям:
. Направляющие косинусы пропорциональны соответствующим проекциям:
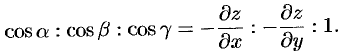
Отсюда 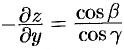 . Тогда
. Тогда
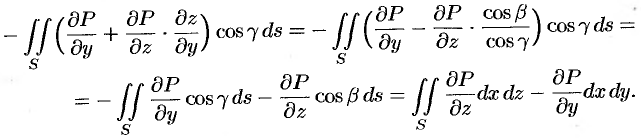
Следовательно,
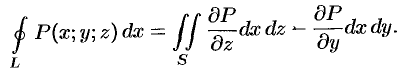
Аналогично получаются при соответствующих условиях еще два равенства:
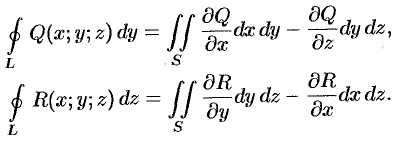
Складывая почленно три последних равенства, получаем формулу Стокса (58.13).
Отметим, что формулу Стокса (58.13) можно применить и для поверхностей более сложного вида (разбив ее на части рассмотренного выше типа).
Формулу Стокса можно применять для вычисления криволинейного интеграла по замкнутому контуру с помощью поверхностного интеграла.
Из формулы Стокса вытекает, что если выполняются условия
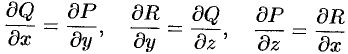
(см. п. 56.4), то криволинейный интеграл по произвольному пространственному замкнутому контуру  равен нулю:
равен нулю: 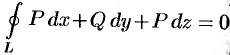 . Следовательно, в данном случае криволинейный интеграл не зависит от вида пути интегрирования.
. Следовательно, в данном случае криволинейный интеграл не зависит от вида пути интегрирования.
Пример №58.3.
Вычислить 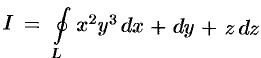 , где контур
, где контур  — окружность
— окружность 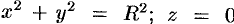 : а) непосредственно, б) используя формулу Стокса, взяв в качестве поверхности полусферу
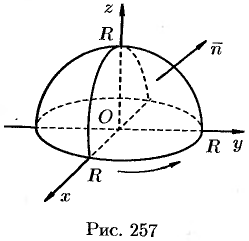
: а) непосредственно, б) используя формулу Стокса, взяв в качестве поверхности полусферу 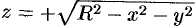 .
.
Решение:
Поверхность интегрирования изображена на рисунке 257.
а) Запишем уравнение окружности в параметрической форме:
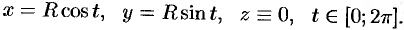
По формуле (56.7) имеем:
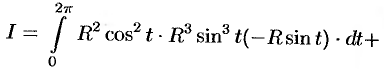
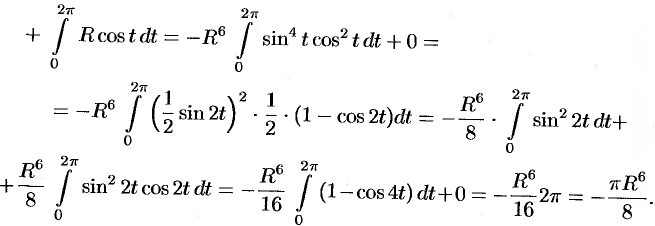
б) По формуле Стокса (58.13) находим:
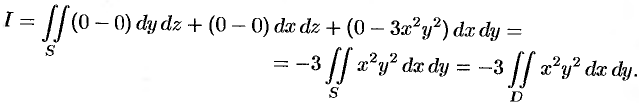
Переходя к полярным координатам, получаем:
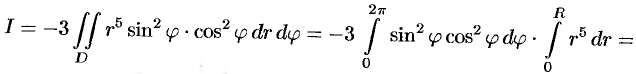
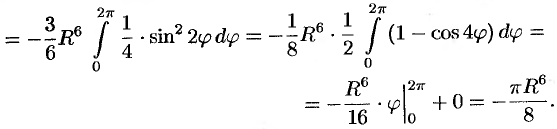
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
