Выпуклость функции. Точки перегиба
Важной геометрической характеристикой функции и кривой, являющейся графиком этой функции, служит выпуклость.
Пусть функция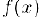 
определена и непрерывна в некотором интервале 
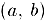. Возьмем точки 
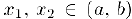и обозначим через 
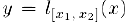уравнение прямой, проходящей через точки 
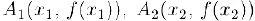графика функции.
Функция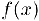 
(соответственно, кривая 
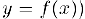называется выпуклой (вогнутой) в интервале 
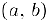, если для любых чисел 
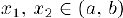выполняется неравенство
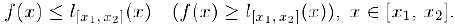
Если последние неравенства строгие для всех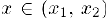 
, то и функция называется строго выпуклой (строго вогнутой).
Геометрически выпуклость (вогнутость) означает, что любой фрагмент графика функции расположен не выше (не ниже), чем хорда соединяющая, граничные точки этого фрагмента.
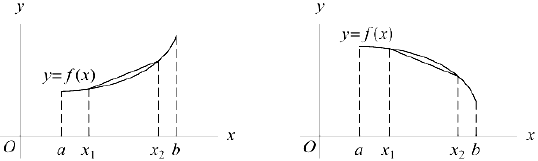
Найдем теперь условия, при которых функция является выпуклой (вогнутой).
Теорема 1 (критерий выпуклости I). Если функция дифференцируема в интервале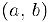 
, то для того, чтобы она была выпуклой (вогнутой), необходимо и достаточно, чтобы производная 
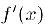была неубывающей (невозрастающей). Если производная 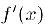возрастает (убывает), то функция 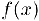строго выпукла (строго вогнута).
Доказательство. Убедимся сначала в необходимости условия теоремы. Предположим для определенности, что функция является выпуклой. Возьмем произвольные точки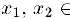 
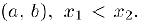— Так как уравнение хорды, соединяющей точки 
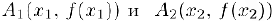мы можем записать в виде
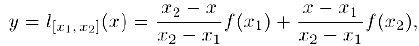
то по определению выпуклости
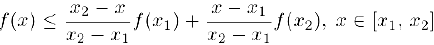
или
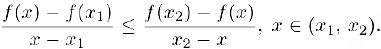
Устремляя в последнем неравенстве переменную х сначала к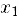 
. а затем к 
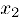, получим: Г
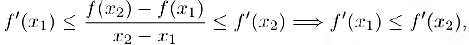
т.е. производная 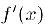не убывает.
Докажем теперь, наоборот, что неубывания производной и достаточно для выпуклости функции. Действительно, применив к обеим частям неравенства (2) теорему Лагранжа (§3). получим:
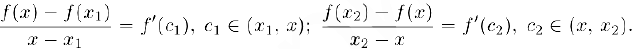
Так как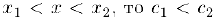 
следовательно, 
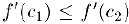. Поэтому неравенство (2), а вслед за ним и неравенство (1) выполняются, т.е. функция 
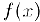выпукла.
Если в рассуждениях предыдущего абзаца считать производную возрастающей, то неравенство (1) будет строгим и, таким образом, функция 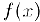будет строго выпуклой.
Теорема доказана.
Привлекая вторую производную, сформулируем еще один признак выпуклости.
Теорема 2 (критерий выпуклости II). Для того, чтобы (функция 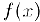, определенная и дважды дифференцируемая в некотором интервале 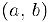была, выпуклой (вогнутой) в этом интервале, необходимо и достаточно, чтобы ее вторая производная была неотрицательной (неположительной) в этом интервале, т.е.. 
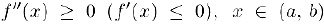. Если же 
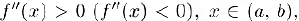, то функция строго выпукла (строго вогнута.) в интервале .
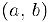Доказательство этой теоремы немедленно следует нз предыдущей теоремы и признака монотонности, доказанного в пункте 1.
Пусть функция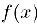 
непрерывна в интервале 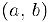. Точка 
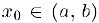называется точкой (строгого) перегиба данной функции, если в интервалах 
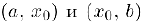эта функция имеет противоположный характер (строгой) выпуклости. Иначе говоря, точка, перегиба является границей двух интервалов, в одном из которых (функция выпукла, а в другом — вогнута.
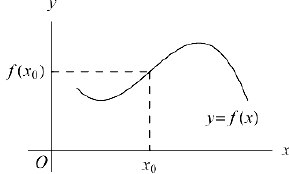
Если функция 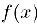дифференцируема в интервале 
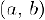, то. как следует из теоремы 1. в точке перегиба 
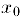производная имеет экстремум. Следовательно, пользуясь признаками экстремума, мы можем сформулировать как необходимый, так и достаточный признаки точки перегиба.
Теорема 3 (необходимый признак точки перегиба). В точке перегиба вторая производная 
не существует или равна нулю.
Таким образом, точка перегиба 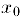является критической точкой для производной 
.
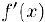Теорема 4 (достаточный признак точки перегиба). Пусть функция 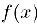дифференцируема в интервале 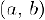и точка 
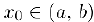является критической для производной. Предположим также, что функция 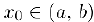дважды дифференцируема в интервале 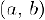за ‘исключением, возможно, точки 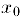. Тогда, если в одном из интервалов 
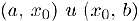вторая производная неотрицательна (положительна), а в другом — неположительна (отрицательна), то 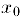— точка перегиба (строгого перегиба) функции .
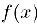Из приведенных теорем следует, это для нахождения точек перегиба функции необходимо найти сначала критические точки ее производной и затем исследовать на перегиб каждую и.з них с помощью достаточного признака.
Эта лекция взята со страницы онлайн помощи по математическому анализу:
Математический анализ онлайн помощь
Возможно эти страницы вам будут полезны:
