Оглавление:
Исследование функций с помощью производных
Определение 1. Функция 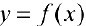 называется возрастающей (убывающей) на интервале
называется возрастающей (убывающей) на интервале 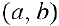 , если
, если 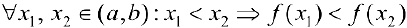
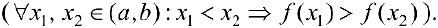
Функция 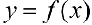 называется неубывающей (невозрастающей) на интервале
называется неубывающей (невозрастающей) на интервале 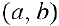 , если
, если 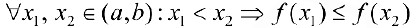
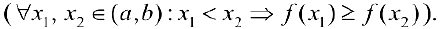
Возрастает:
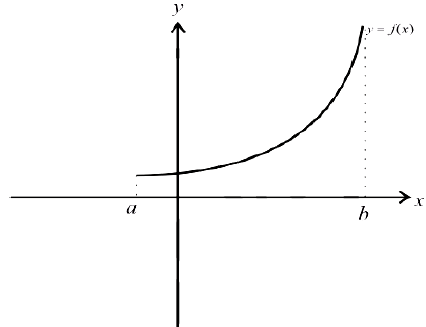
Убывает:
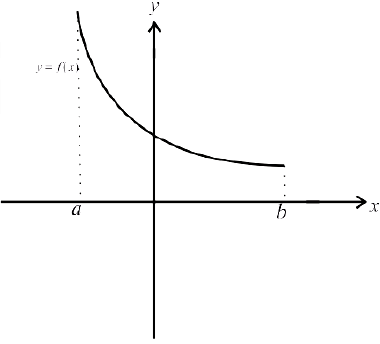
Неубывает:
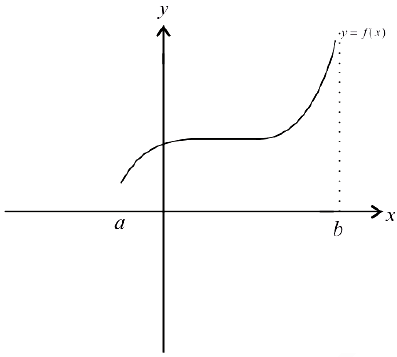
Невозрастает:
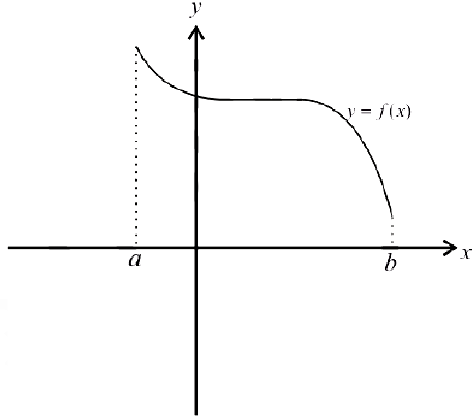
Функции из определения 1 называются монотонными.
Теорема 1. Для того, чтобы дифференцируемая на интервале 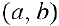 функция
функция 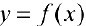 не убывала (не возрастала) па этом интервале необходимо и достаточно, чтобы
не убывала (не возрастала) па этом интервале необходимо и достаточно, чтобы 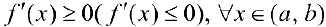 .
.
Доказательство. Необходимость. Рассмотрим случай, когда 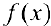 не убывает и докажем, что производная
не убывает и докажем, что производная 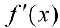 необходимо
необходимо 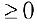 .
.
Пусть 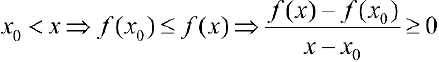 .
.
Пусть 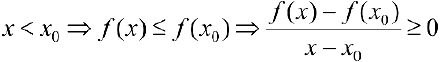 .
.
Таким образом 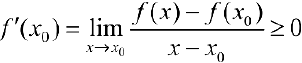 , что и требовалось доказать.
, что и требовалось доказать.
Достаточность. Рассмотрим случай, когда 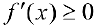 и докажем, что этого достаточно для того, чтобы функция не убывала. Пусть
и докажем, что этого достаточно для того, чтобы функция не убывала. Пусть 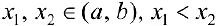 . Тогда по теореме Лагранжа (теорема 4 § 12)
. Тогда по теореме Лагранжа (теорема 4 § 12) 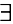 точка
точка 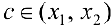 такая, что
такая, что 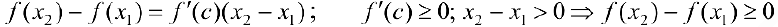 что и требовалось доказать.
что и требовалось доказать.
Теорема 2. Для того, чтобы дифференцируемая на интервале 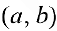 функция
функция 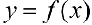 возрастала (убывала) на этом интервале достаточно, чтобы
возрастала (убывала) на этом интервале достаточно, чтобы 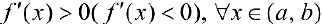 .
.
Доказательство теоремы аналогично доказательству достаточности в теореме 1. Нужно заметить, что условие 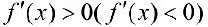 не является необходимым для возрастания (убывания) функции.
не является необходимым для возрастания (убывания) функции.
Задача №1
Рассмотрим функцию 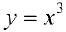 . Она возрастает на промежутке (-1; 1). Но условие
. Она возрастает на промежутке (-1; 1). Но условие 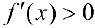 не выполнено в точке
не выполнено в точке 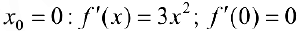 .
.
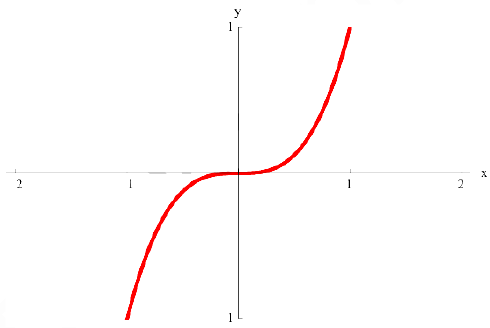
Теорема 3. (необходимое условие экстремума).
Пусть функция 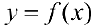 определена в некоторой окрестности точки
определена в некоторой окрестности точки 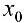 и имеет в этой точке локальный экстремум(см. определение 1 §12). Тогда ее производная в этой точке равна 0 или не существует.
и имеет в этой точке локальный экстремум(см. определение 1 §12). Тогда ее производная в этой точке равна 0 или не существует.
Доказательство. Если производная 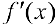 в точке
в точке 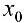 не существует, то все доказано. Предположим, что
не существует, то все доказано. Предположим, что 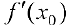 — существует. Тогда по теореме Ферма (теорема 1 §12)
— существует. Тогда по теореме Ферма (теорема 1 §12) 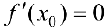 , что и требовалось доказать.
, что и требовалось доказать.
Определение 2. Пусть функция 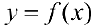 непрерывна в точке
непрерывна в точке 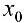 и производная
и производная 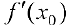 равна 0 или не существует. Тогда точка
равна 0 или не существует. Тогда точка 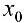 называется критической точкой для функции
называется критической точкой для функции  или точкой возможного экстремума.
или точкой возможного экстремума.
Замечание. Для непрерывной функции любая точка локального экстремума будет критической. Наоборот — не верно.
Задача №2
Для функции 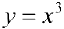 , точка
, точка 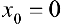 — критическая, но не является точкой локального экстремума.
— критическая, но не является точкой локального экстремума.
Для функции 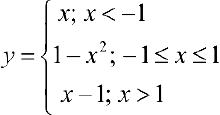
(см. пример 9 §5) 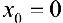 — критическая и локальный максимум;
— критическая и локальный максимум; 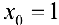 -критическая и локальный минимум.
-критическая и локальный минимум.
Для функции 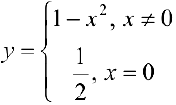
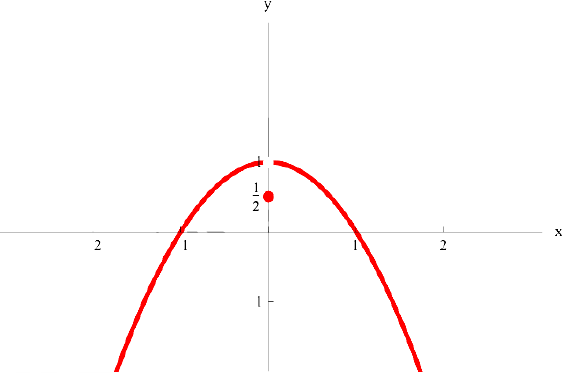
точка 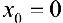 — локального минимума, производная
— локального минимума, производная 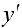 в точке
в точке 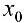 не существует. Точка
не существует. Точка 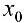 не является критической( в точке
не является критической( в точке 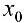 — разрыв 1-ого рода).
— разрыв 1-ого рода).
Для функции 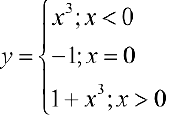
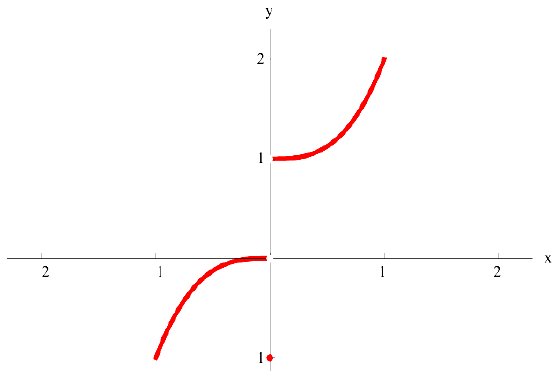
точка 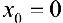 — точка локального минимума. Точка
— точка локального минимума. Точка 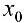 не является критической в точке
не является критической в точке 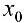 — разрыв 1-ого рода).
— разрыв 1-ого рода).
Теорема 4. (достаточное условие экстремума функции). Пусть функция 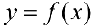 дифференцируема в некоторой окрестности
дифференцируема в некоторой окрестности 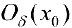 своей критической точки
своей критической точки 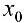 за исключением может быть самой точки
за исключением может быть самой точки 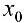 .
.
а) Пусть при переходе через точку 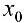 производная
производная 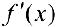 меняет знак с «-» на «+» :
меняет знак с «-» на «+» :
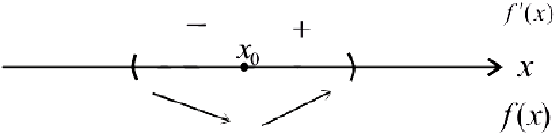
Тогда  — точка локального минимума .
— точка локального минимума .
Пусть при переходе через точку  производная
производная  меняет знак с «+»на «-» :
меняет знак с «+»на «-» :
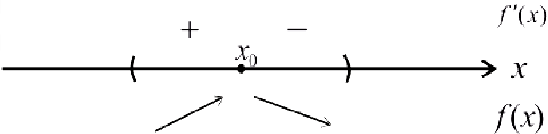
Тогда 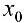 — точка локального максимума.
— точка локального максимума.
б) Пусть при переходе через точку 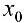 производная
производная 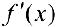 не меняет знака. Тогда
не меняет знака. Тогда 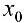 не является точкой локального экстремума.
не является точкой локального экстремума.
Доказательство следует из теоремы 2. При этом важно, чтобы функция 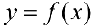 была непрерывна в точке
была непрерывна в точке 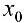 (см. пример 2), а также то, что
(см. пример 2), а также то, что 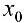 — изолированная критическая точка.
— изолированная критическая точка.
Теорема 5. (второе достаточное условие экстремума функции).
Пусть 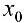 — стационарная точка для функции
— стационарная точка для функции 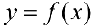 , то есть
, то есть 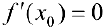 . Пусть
. Пусть 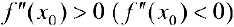 . Тогда
. Тогда 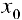 — точка локального минимума (локального максимума).
— точка локального минимума (локального максимума).
Доказательство. Запишем формулу Тейлора 2-ого порядка для функции 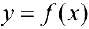 в окрестности точки
в окрестности точки 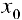 :
:
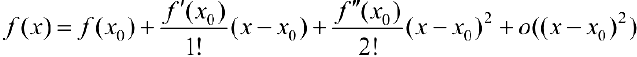
(см. теорему 1 §14).
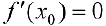 поэтому из (1) следует:
поэтому из (1) следует:
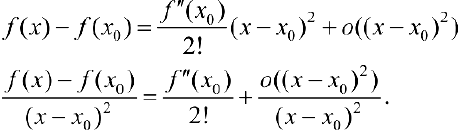
Из (2) следует, что 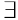 окрестность точки
окрестность точки 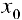 , такая что знак
, такая что знак 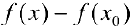 совпадает со знаком
совпадает со знаком 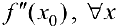 из этой окрестности, что и требовалось доказать.
из этой окрестности, что и требовалось доказать.
Теорема 6. Пусть функция 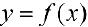 имеет в точке
имеет в точке 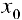 n производных, причем
n производных, причем
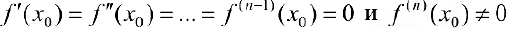 Тогда:
Тогда:
1) если n — четное и 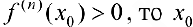 — точка локального минимума;
— точка локального минимума;
2) если n — четное и 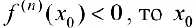 — точка локального максимума;
— точка локального максимума;
3) если n — нечетное, то в точке 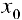 локального экстремума нет.
локального экстремума нет.
Доказательство аналогично доказательству теоремы 5.
| Решение задач по математическому анализу |
Задача №3
Исследовать на экстремум функцию 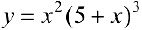 .
.
Решение:
Функция непрерывна  .
.
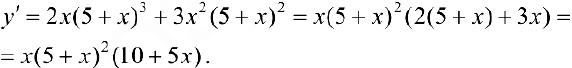
Найдем критические точки: 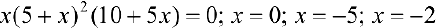 .
.
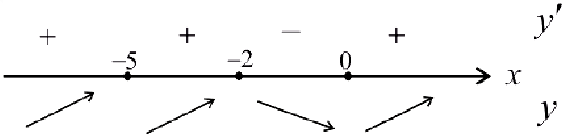
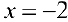 — точка локального максимума:
— точка локального максимума: 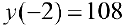 ;
;
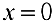 — точка локального минимума;
— точка локального минимума; 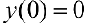 .
.
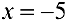 — не является точкой экстремума.
— не является точкой экстремума.
При исследовании функции на экстремум точки разрыва(если они есть) также наносят на числовую прямую. При переходе через эти точки может изменятся направление возрастания (убывания) функции.
Упражнение 1. Исследовать на экстремум функции:
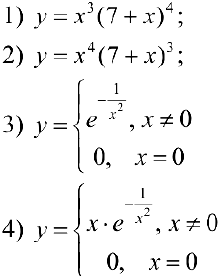
Замечание. При решении ряда технических и экономических задач приходится находить не локальные, а глобальные экстремумы( наибольшие и наименьшие значения функций на некотором множестве). Из теоремы Вейерштрасса(см.теорему 1 § 11) следует, что для непрерывной функции 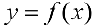 заданной на отрезке
заданной на отрезке 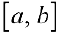 глобальные min и max существуют. При этом точки
глобальные min и max существуют. При этом точки 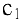 и
и 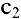 — глобального min и max лежат либо на концах отрезка
— глобального min и max лежат либо на концах отрезка 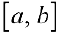 , либо являются критическими для функции
, либо являются критическими для функции 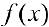 .
.
Задача №4
Найти наибольшее и наименьшее значение функции 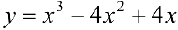 на отрезке [0, 3].
на отрезке [0, 3].
Решение:
Функция непрерывна 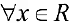 . Найдем критические точки:
. Найдем критические точки:
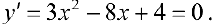
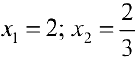 — критические точки.
— критические точки.
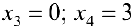 — концы отрезка.
— концы отрезка.
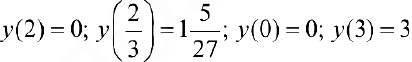
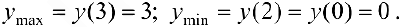
Задача №5
Боковые стороны и меньшее основание трапеции 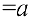 . Найти длину большего основания, при котором площадь трапеции — наибольшая.
. Найти длину большего основания, при котором площадь трапеции — наибольшая.
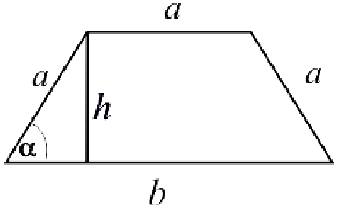
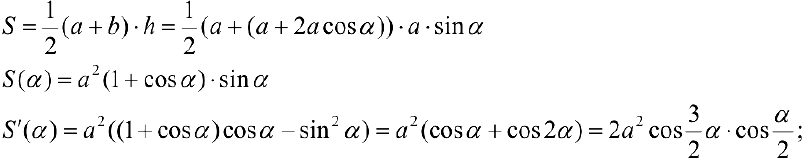
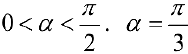 — критическая точка для функции
— критическая точка для функции 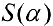 .
.
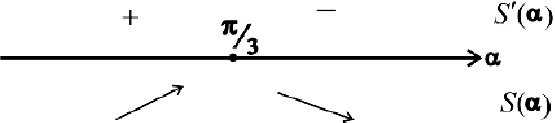
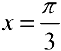 — точка локального максимума.
— точка локального максимума.
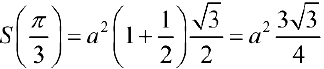 — наибольшее значение площади, при этом
— наибольшее значение площади, при этом 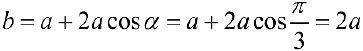 — длина большего основания.
— длина большего основания.
Определение 1. Пусть функция 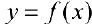 дифференцируема на интервале
дифференцируема на интервале 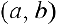 . И пусть
. И пусть 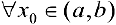 график функции
график функции 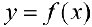 расположен ниже (не выше), чем касательная
расположен ниже (не выше), чем касательная 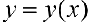 к нему в точке
к нему в точке 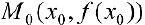 , то есть
, то есть 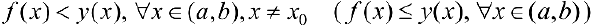 . Тогда
. Тогда 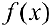 называется выпуклой(нестрого выпуклой вверх).
называется выпуклой(нестрого выпуклой вверх).
Пусть 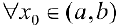 график функции
график функции 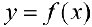 расположен выше (не ниже), чем касательная
расположен выше (не ниже), чем касательная 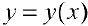 к нему в точке
к нему в точке 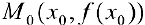 , то есть
, то есть 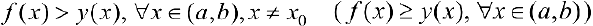 ). Тогда
). Тогда 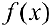 называется вогпутой(нестрого вогнутой).
называется вогпутой(нестрого вогнутой).
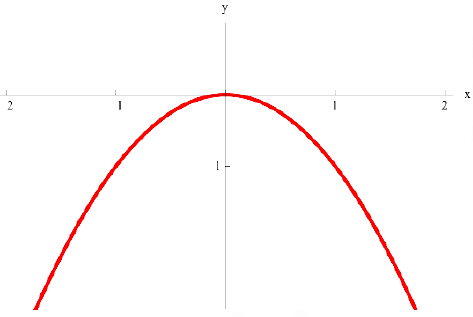
Задача №6
а) 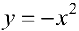 выпукла на всей оси
выпукла на всей оси 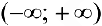 ;
;
б) 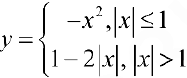 нестрого выпукла вверх на всей оси
нестрого выпукла вверх на всей оси 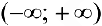
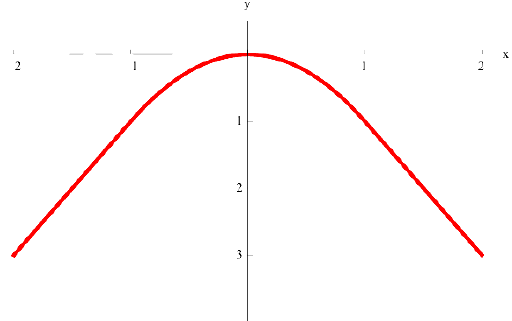
в) 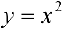 вогнута па всей оси
вогнута па всей оси  :
:
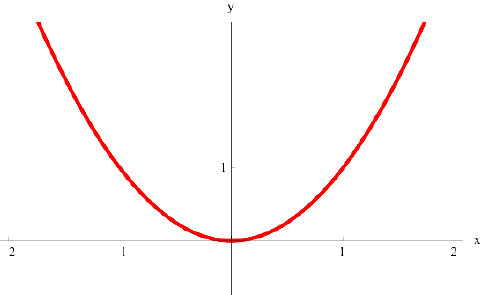
r)  нестрого вогнута на всей оси
нестрого вогнута на всей оси 
Теорема 1. Для того, чтобы дифференцируемая функция  была вогнутой (выпуклой) на интервале
была вогнутой (выпуклой) на интервале 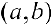 необходимо и достаточно, чтобы ее производная
необходимо и достаточно, чтобы ее производная 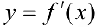 возрастала(убывала) на этом интервале.
возрастала(убывала) на этом интервале.
Докажем для случая, когда 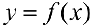 — вогнута.
— вогнута.
Необходимость. Пусть 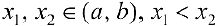 ,
,
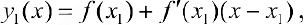
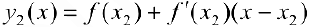 — касательные к графику
— касательные к графику 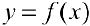 в точках
в точках 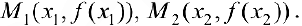 . Так как
. Так как 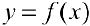 ) — вогнута, то
) — вогнута, то
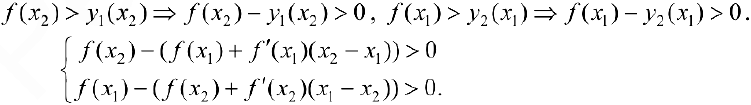
Сложим эти неравенства:
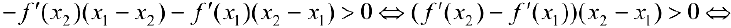
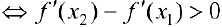 что и требовалось доказать.
что и требовалось доказать.
Достаточность. Пусть 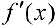 — возрастает. Докажем, что
— возрастает. Докажем, что 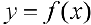 — вогнута. Пусть
— вогнута. Пусть 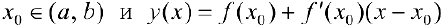 — уравнение касательной в точке
— уравнение касательной в точке 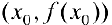 . Пусть
. Пусть 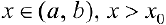 . Найдем разность
. Найдем разность 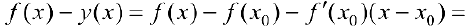
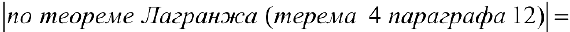
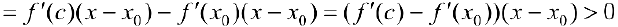 что и требовалось доказать.
что и требовалось доказать.
Теорема 2. Для того, чтобы дифференцируемая функция 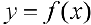 была нестрого вогнутой (пестрого выпуклой) на интервале
была нестрого вогнутой (пестрого выпуклой) на интервале 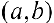 необходимо и достаточно, чтобы производная
необходимо и достаточно, чтобы производная 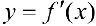 неубывала (невозрастала) на этом интервале.
неубывала (невозрастала) на этом интервале.
Доказательство аналогично доказательству теоремы 1.
Теорема 3. Для того, чтобы дважды дифференцируемая на интервале 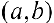 функция
функция 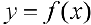 была не строго вогнутой (не строго выпуклой) необходимо и достаточно, чтобы
была не строго вогнутой (не строго выпуклой) необходимо и достаточно, чтобы 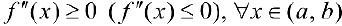 .
.
Доказательство следует из теоремы 2 и теоремы 1 §15.
Теорема 4. Для того, чтобы дважды дифференцируемая па интервале 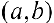 функция
функция 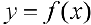 была вогнутой (выпуклой) на этом интервале достаточно, чтобы
была вогнутой (выпуклой) на этом интервале достаточно, чтобы 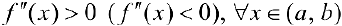 .
.
Доказательство следует из теоремы 1 и теоремы 2 §15. Нужно заметить, что условие 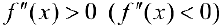 не является необходимым для вогнутости(выпуклости) функции.
не является необходимым для вогнутости(выпуклости) функции.
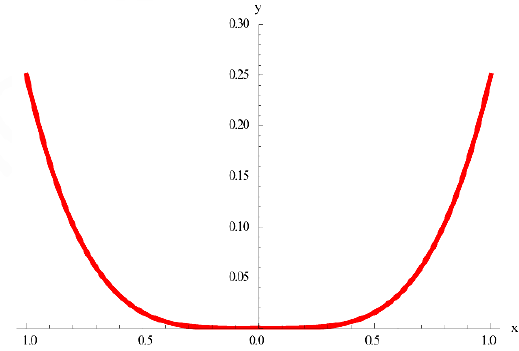
Задача №7
Рассмотрим функцию 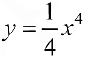 . Она вогнута на интервале (-1; 1).
. Она вогнута на интервале (-1; 1).
Но условие 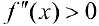 не выполнено в точке
не выполнено в точке 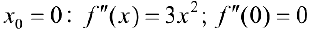 .
.
Определение 2. Пусть функция 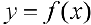 имеет касательную в точке
имеет касательную в точке 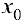 (см. определение!, 2 § 9, определение 5 §6) и пусть при переходе через точку
(см. определение!, 2 § 9, определение 5 §6) и пусть при переходе через точку 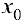 направление выпуклости меняется на противоположное. Тогда точка
направление выпуклости меняется на противоположное. Тогда точка 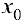 называется точкой перегиба.
называется точкой перегиба.
Теорема 5 (необходимое условие точки перегиба). Пусть 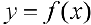 дифференцируема в некоторой окрестности точки
дифференцируема в некоторой окрестности точки 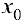 за исключением может быть самой точки
за исключением может быть самой точки 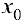 и точка
и точка 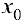 является точкой перегиба. Тогда ее вторая производная
является точкой перегиба. Тогда ее вторая производная 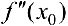 в этой точке равна 0 или не существует.
в этой точке равна 0 или не существует.
Доказательство. Если 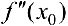 не существует, то все доказано. Предположим, что
не существует, то все доказано. Предположим, что 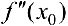 существует. Тогда
существует. Тогда 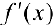 — непрерывна в точке
— непрерывна в точке 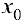 и, так как
и, так как 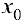 — точка перегиба, то согласно теореме 1,
— точка перегиба, то согласно теореме 1, 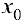 — точка локального экстремума для функции
— точка локального экстремума для функции 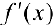 , поэтому по теореме 3 §15
, поэтому по теореме 3 §15 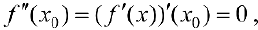 , что и требовалось доказать.
, что и требовалось доказать.
Определение 3. Пусть вторая производная 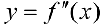 функции
функции 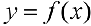 равна 0 или не существует в точке
равна 0 или не существует в точке 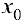 и пусть функция
и пусть функция 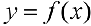 имеет касательную в точке
имеет касательную в точке 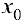 . Тогда точка
. Тогда точка 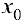 называется точкой возможного перегиба.
называется точкой возможного перегиба.
Замечание. Согласно теореме 5 для дифференцируемой функции 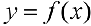 любая точка перегиба будет удовлетворять определению 3. Наоборот неверно.
любая точка перегиба будет удовлетворять определению 3. Наоборот неверно.
Для функции 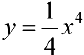 из примера 2 точка
из примера 2 точка 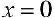 — точка возможного перегиба, но эта точка не будет точкой перегиба.
— точка возможного перегиба, но эта точка не будет точкой перегиба.
Теорема 6 (достаточное условие перегиба функции). Рассмотрим функцию 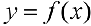 дважды дифференцируемую в некоторой окрестности
дважды дифференцируемую в некоторой окрестности 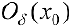 точки возможного перегиба
точки возможного перегиба 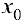 за исключением может быть самой точки
за исключением может быть самой точки 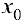 . Предположим также, что вторая производная
. Предположим также, что вторая производная 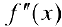 меняет знак при переходе через точку
меняет знак при переходе через точку 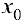 . Тогда
. Тогда 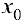 будет точкой перегиба для функции
будет точкой перегиба для функции 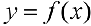 —
—
Доказательство следует из теоремы 4.
Задача №8
Найдем точки перегиба и интервалы выпуклости-вогнутости функции 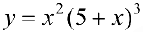 из примера 3 §15.
из примера 3 §15.
Решение:
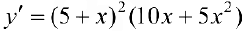 (см. пример 3 §15).
(см. пример 3 §15).
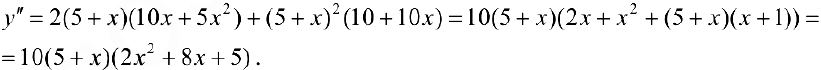
Найдем точки возможного перегиба (точки, где 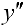 равна 0 или не существует).
равна 0 или не существует).
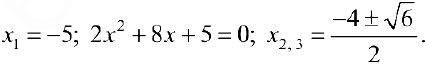
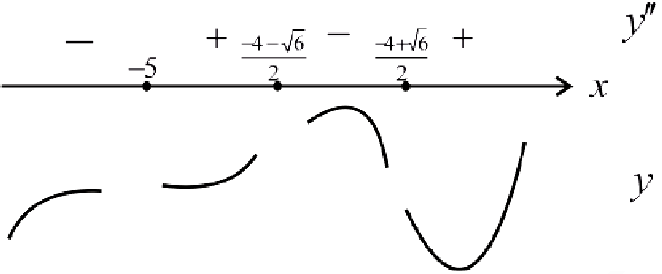
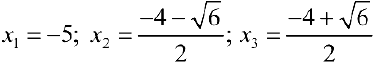 — точки перегиба функции.
— точки перегиба функции.
При нахождении интервалов выпуклости-вогнутости точки, где функции  имеют разрывы также наносят па числовую прямую. При переходе через эти точки может меняться направление выпуклости-вогнутости.
имеют разрывы также наносят па числовую прямую. При переходе через эти точки может меняться направление выпуклости-вогнутости.
Определение 4. Прямая 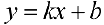 называется наклонной асимптотой функции
называется наклонной асимптотой функции 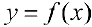 при
при 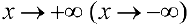 , если
, если 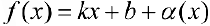 , где
, где 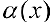 бесконечно-малая функция при
бесконечно-малая функция при 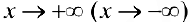 , то есть
, то есть
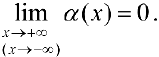
Теорема 7. Для того, чтобы прямая 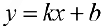 была наклонной асимптотой для функции
была наклонной асимптотой для функции 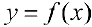 при
при 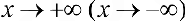 необходимо и достаточно, чтобы существовали пределы
необходимо и достаточно, чтобы существовали пределы
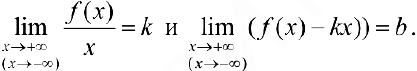
Доказательство. Рассмотрим, например, случай 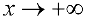 .
.
Необходимость. Пусть 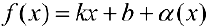 , где
, где 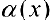 бесконечно-малая функция. Докажем, что выполняются пределы (1).
бесконечно-малая функция. Докажем, что выполняются пределы (1).
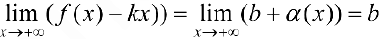
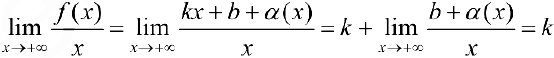 что и требовалось доказать.
что и требовалось доказать.
Достаточность. Пусть выполняется (1). Докажем, что 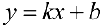 — асимптота для
— асимптота для 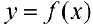 .
.
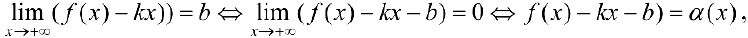 где
где 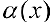 бесконечно-малая функция при
бесконечно-малая функция при 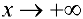 , что и требовалось доказать. Таким образом теорема доказана.
, что и требовалось доказать. Таким образом теорема доказана.
Замечание. Наличие наклонной асимптоты значит, что при 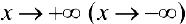 график функции очень близок к прямой линии
график функции очень близок к прямой линии 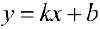 .
.
Задача №9
Для функции 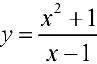 (см. пример I §5)
(см. пример I §5) 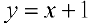 — наклонная асимптота при
— наклонная асимптота при 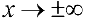 .
.
Для функции 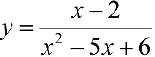 (пример 8 §5)
(пример 8 §5) 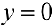 — горизонтальная асимптота при
— горизонтальная асимптота при 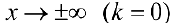 .
.
Для функции 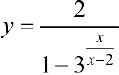 (пример 10 §5)
(пример 10 §5) 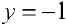 — горизонтальная асимптота при
— горизонтальная асимптота при 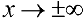 .
.
Для функции 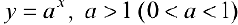 (пример 2 §5)
(пример 2 §5) 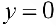 — горизонтальная асимптота при
— горизонтальная асимптота при 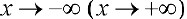 .
.
Определение 5. Прямая 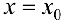 называется вертикальной асимптотой функции
называется вертикальной асимптотой функции 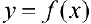 , если хотя бы один из пределов
, если хотя бы один из пределов 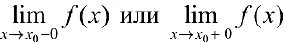 равен
равен 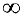 .
.
Задача №10
Для функции 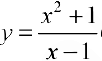 (см. пример 1 §5) прямая
(см. пример 1 §5) прямая 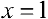 — вертикальная асимптота, для функции
— вертикальная асимптота, для функции 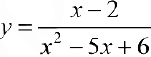 (пример 8 §5) прямая
(пример 8 §5) прямая 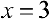 — — вертикальная асимптота, для функции
— — вертикальная асимптота, для функции 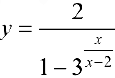 (пример 10 §5) прямая
(пример 10 §5) прямая 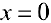 — вертикальная асимптота, для функции
— вертикальная асимптота, для функции 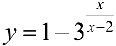 из упражнения 1 §5 прямая
из упражнения 1 §5 прямая 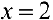 — вертикальная асимптота
— вертикальная асимптота 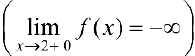 .
.
При построении графиков функции используют результаты §15, 16. Это можно проводить по следующей схеме:
- Найти область определения
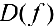 функции и исследовать поведение функции в граничных точках
функции и исследовать поведение функции в граничных точках 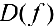 . Определить точки разрыва, вертикальные асимптоты, нули функции, исследовать функцию на периодичность, четность, нечетность.
. Определить точки разрыва, вертикальные асимптоты, нули функции, исследовать функцию на периодичность, четность, нечетность. - Найти наклонные асимптоты.
- Найти интервалы монотонности, точки локального экстремума.
- Найти интервалы выпуклости, вогнутости, точки перегиба.
- Построить график.
Задача №11
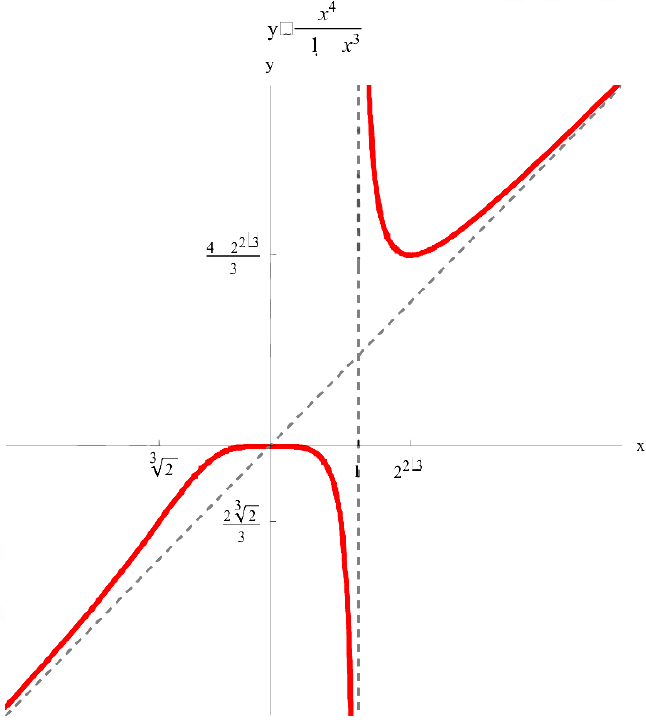
Провести полное исследование и построить график функции 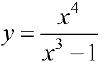 .
.
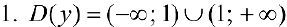
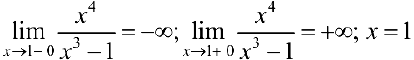 — вертикальная асимптота.
— вертикальная асимптота.
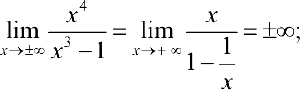
Нули функции: 
Таким образом график пересекает оси координат в точке 0(0; 0). Функция ни четная, ни нечетная, не периодическая.
2. Наклонные асимптоты. По формулам (1);
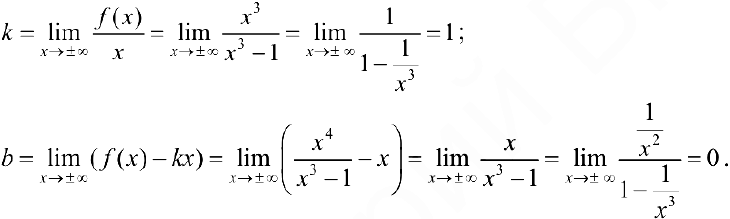
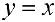 — наклонная асимптота при
— наклонная асимптота при 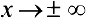 .
.
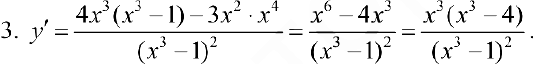
Точки, где 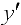 равна 0 или не существует:
равна 0 или не существует: 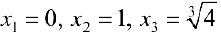 .
.

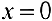 — точка локального максимума;
— точка локального максимума; 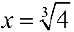 — точка локального минимума;
— точка локального минимума;
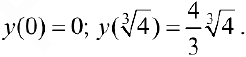
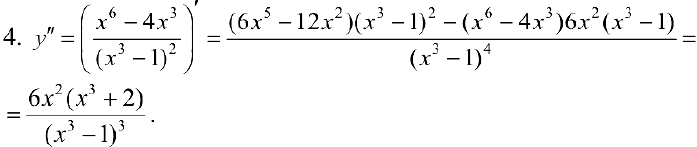
Точки где 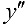 равна 0 или не существует:
равна 0 или не существует: 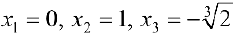 .
.

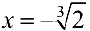
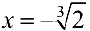 — точка перегиба;
— точка перегиба; 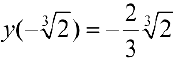 .
.
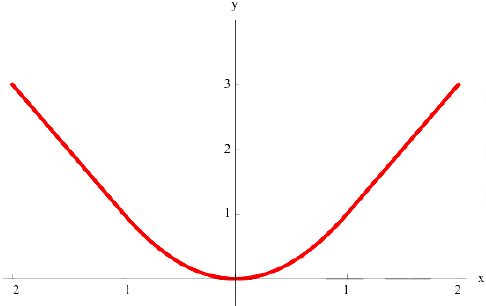
5. График функции.
Эта теория и задачи с решением взяты со страницы готовых задач с решением по математическому анализу:
Решение задач по математическому анализу
Возможно эти темы вам будут полезны:
