Оглавление:
Неопределенный интеграл
Определение 1. Пусть  — промежуток действительной оси. Функция
— промежуток действительной оси. Функция 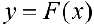 называется первообразной для функции
называется первообразной для функции 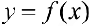 на промежутке
на промежутке  , если
, если 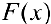 — дифференцируема на
— дифференцируема на  и
и
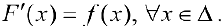
Задача №12
a) 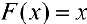 — первообразная для
— первообразная для 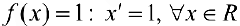 .
.
б) 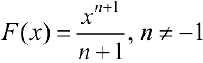 — первообразная для
— первообразная для 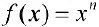 :
:
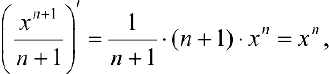 на любом промежутке из области определения функции
на любом промежутке из области определения функции 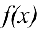 .
.
в) 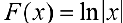 — первообразная для
— первообразная для 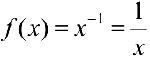 . Действительно,
. Действительно,
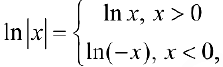 и
и 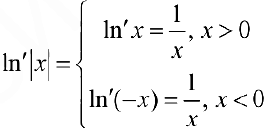 — на любом промежутке, не содержащем точку 0.
— на любом промежутке, не содержащем точку 0.
Упражнение 1. Найти первообразную для функций:
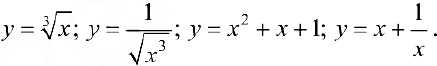
Упражнение 2. 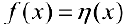 — единичная функция Хевисайда (см. пример 4 §5). Найти первообразные для
— единичная функция Хевисайда (см. пример 4 §5). Найти первообразные для 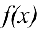 :
:
1) на промежутке (0, 2); 2) на промежутке (- 2, 0); 3) на промежутке (- 2; 2).
Упражнение 3. 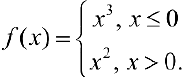 Найти первоооразные для
Найти первоооразные для 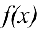 на промежутках (0,2); (- 2, 0); (- 2; 2).
на промежутках (0,2); (- 2, 0); (- 2; 2).
Замечание. Первообразная функция определена не однозначно. А именно, 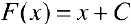 , где С — любая константа также будет первообразной для
, где С — любая константа также будет первообразной для 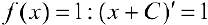 .
.
В общем случае верна теорема:
Теорема 1. Две дифференцируемые на промежутке  функции
функции 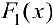 и
и 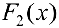 будут первообразными для одной и той же функции
будут первообразными для одной и той же функции 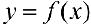 тогда и только тогда, когда
тогда и только тогда, когда 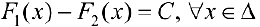 .
.
Доказательство. Необходимость. 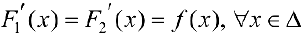 . Докажем, что они отличаются на константу. Пусть
. Докажем, что они отличаются на константу. Пусть 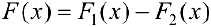 .
.
Тогда 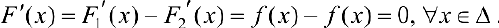 . Пусть
. Пусть 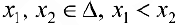 . По теореме Лагранжа (теорема 4 § 12):
. По теореме Лагранжа (теорема 4 § 12):
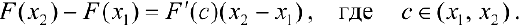 Но
Но 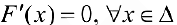 , поэтому
, поэтому 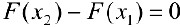 , то есть
, то есть 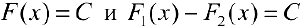 , что и требовалось.
, что и требовалось.
Достаточность. 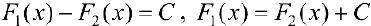 . Обозначим
. Обозначим 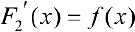 . Тогда
. Тогда 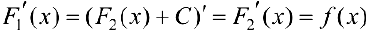 , то есть
, то есть 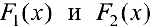 — первообразные для одной и той же функции
— первообразные для одной и той же функции 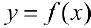 , что и требовалось доказать.
, что и требовалось доказать.
Определение 2. Множество всех первообразных для функции 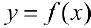 на промежутке
на промежутке  называется неопределенным интегралом от функции
называется неопределенным интегралом от функции 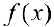 и обозначается
и обозначается 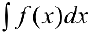
Если 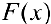 — одна из первообразных, то , согласно теореме 1,
— одна из первообразных, то , согласно теореме 1,
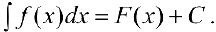
Свойства неопределенного интеграла.
1. Если 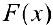 — дифференцируема на
— дифференцируема на  , то
, то 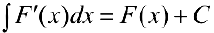 ,
,
или 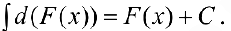 .
.
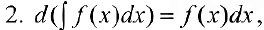
здесь под записью 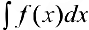 подразумеваем одну из первообразных.
подразумеваем одну из первообразных.
3. Если 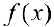 имеет первообразную на
имеет первообразную на  , то
, то 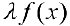 также имеет первообразную на
также имеет первообразную на  и ,если
и ,если 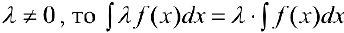
4. Если 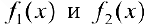 имеют первообразную на
имеют первообразную на  , тогда
, тогда 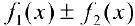 также имеет первообразную на
также имеет первообразную на  и:
и:
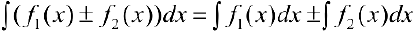
Свойства 1 — 4 легко выводятся из определения первообразной и интеграла и соответствующих свойств производной.
Докажем, например, свойство 3.
Пусть 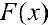 — первообразная для
— первообразная для 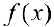 на промежутке
на промежутке  . Тогда
. Тогда 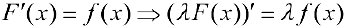 то есть
то есть 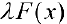 — первообразная для
— первообразная для 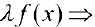
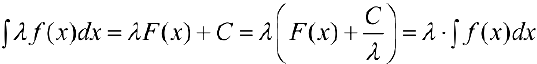 что и требовалось доказать.
что и требовалось доказать.
Из определений 1,2 следует, что интегрирование — действие обратное дифференцированию (находится функция, производная которой равна данной).
Таблица интегралов
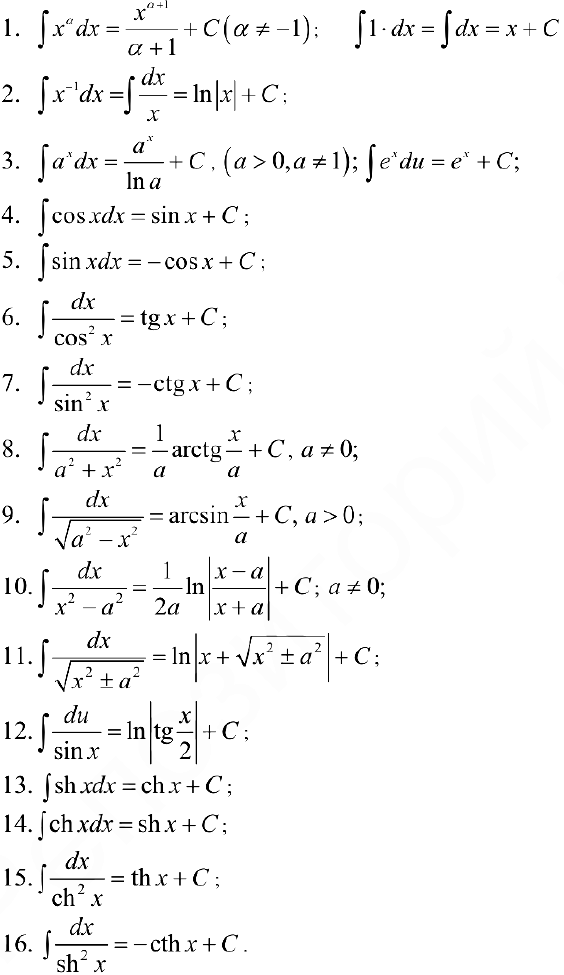
При вычислении интегралов в простых случаях применяют свойства 1 — 4.
Задача №13
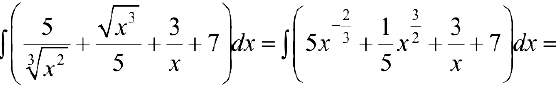
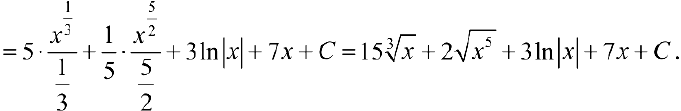
Задача №14
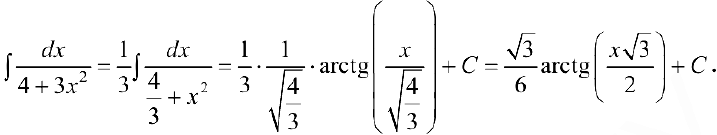
Теорема 1. Если 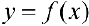 — непрерывна на промежутке
— непрерывна на промежутке 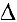 , то для нее
, то для нее 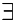 первообразная функция
первообразная функция 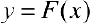 на этом промежутке.
на этом промежутке.
Эта теория и задачи с решением взяты со страницы готовых задач с решением по математическому анализу:
Решение задач по математическому анализу
Возможно эти темы вам будут полезны:
