Оглавление:

| Здравствуйте! Я Людмила Анатольевна Фирмаль, занимаюсь помощью студентам более 17 лет. У меня своя команда грамотных, сильных преподавателей. Мы справимся с любой поставленной перед нами работой технического и гуманитарного плана. И неважно – она по объёму на две формулы или огромная, сложно структурированная, на 125 страниц! Нам по силам всё, поэтому не стесняйтесь, присылайте. |
| Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу! |
Как заказать выполнение заданий по математике
Вы можете написать сообщение в WhatsApp. После этого я оценю ваш заказ и укажу стоимость и срок выполнения вашей работы. Если условия Вас устроят, Вы оплатите, и преподаватель, который ответственен за вашу работу, начнёт выполнение и в согласованный срок или, возможно, раньше срока Вы получите файл готовой работы в личные сообщения.
Сколько может стоить заказ математики
Стоимость заказа зависит от задания и требований Вашего учебного заведения. На цену влияют: сложность, количество заданий и срок выполнения. Поэтому для оценки стоимости заказа максимально качественно сфотографируйте или пришлите файл задания, при необходимости, загружайте поясняющие фотографии лекций, файлы методичек, указывайте свой вариант.
Какой срок выполнения заказа
Минимальный срок выполнения заказа составляет 2-4 дня, но помните, срочные задания оцениваются дороже.
Как оплатить заказ
Сначала пришлите задание, я оценю, после вышлю вам форму оплаты, в которой можно оплатить с баланса мобильного телефона, картой Visa и MasterCard, apple pay, google pay.
Гарантии и исправление ошибок
В течение 1 года с момента получения Вами готового решения заказа действует гарантия. В течении 1 года я и моя команда исправим любые ошибки в заказе.
Чуть ниже я предоставила теорию для того чтобы вы освежили свои знания и примеры оформления работ по математике, так я буду оформлять ваши работы если закажите у меня.
Элементы теории чисел
Целые числа. Делимость и остатки Теоретический материал
При решении задач на целые числа необходимо знать следующие факты:
- любое натуральное число единственным образом (с точностью до перестановки сомножителей) может быть представлено в виде произведения простых чисел;
- при делении натурального числа
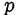 на натуральное число
на натуральное число 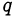 возможны
возможны 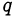 различных остатков: 0,1, 2,…, (
различных остатков: 0,1, 2,…, (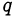 — 1).
— 1).
Полезно также помнить признаки делимости натуральных чисел:
- при делении на 5 и на 10 число даёт такой же остаток, как и последняя его цифра;
- при делении на 4, 25, 50 и на 100 число даёт такой же остаток, как и число, записанное двумя его последними цифрами;
- при делении на 3 и на 9 число даёт такой же остаток, как и сумма его цифр. Поэтому, если сумма цифр делится на 3 или на 9, то и само число делится на 3 или на 9.
Заметим, что при изучении делимости чисел достаточно работать не с самими числами, а с остатками от деления этих чисел. Все арифметические действия с остатками, кроме деления, повторяют действия с числами, а именно: при сложении чисел складываются остатки, при возведении в степень в эту степень возводятся остатки и т.д.
В задачах, где требуется установить, что какое-то выражение, зависящее от натурального числа 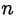 , делится или не делится при всех
, делится или не делится при всех 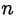 на заданное натуральное число, часто используется следующий факт: произведение
на заданное натуральное число, часто используется следующий факт: произведение 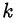 последовательных натуральных чисел делится на
последовательных натуральных чисел делится на 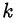 .
.
Эта ссылка возможно вам будет полезна:
| Предмет математика полный курс лекций |
Пример оформления заказа №1.
Остатки от деления на 3 чисел тип равны 1 и 2 соответственно. Каковы остатки от деления на 3:
а) суммы 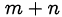 ;
;
б) произведения 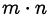 ?
?
Решение:
Так как 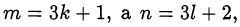 то
то

Следовательно, 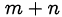 делится на 3 нацело. Рассмотрим теперь произведение
делится на 3 нацело. Рассмотрим теперь произведение
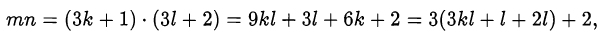
то есть при делении на 3 произведения топ остаток равен 2. Ответ, а) 0, б) 2.
Пример оформления заказа №2.
Доказать, что для всех натуральных 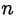 выражение
выражение 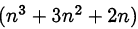 делится на 6.
делится на 6.
Решение:
Так как 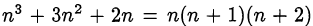 — есть произведение трёх последовательных чисел, которое всегда делится и на 2, и на 3, то
— есть произведение трёх последовательных чисел, которое всегда делится и на 2, и на 3, то 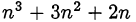 делится на 6.
делится на 6.
Пример оформления заказа №3.
Дано число 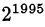 . Найти
. Найти
а) последнюю цифру этого числа,
б) остаток от деления на 7.
Решение:
а) Представим исходное число в виде
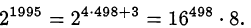
Поскольку 16 в любой натуральной степени оканчивается на б, а 6 • 8 = 48, последняя цифра числа 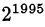 равна 8.
равна 8.
б) Рассмотрим остатки степеней двойки от деления на 7:
-
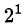 при делении на 7 даёт остаток 2,
при делении на 7 даёт остаток 2, -
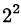 при делении на 7 даёт остаток 4,
при делении на 7 даёт остаток 4, -
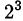 при делении на 7 даёт остаток 1.
при делении на 7 даёт остаток 1.
Эти остатки повторяются с периодом 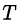 = 3. Так как 1995 = 3 • 665, то
= 3. Так как 1995 = 3 • 665, то 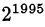 при делении на 7 даёт остаток 1.
при делении на 7 даёт остаток 1.
Ответ, а) 8, б) 1.
Уравнения в целых числах
Теоретический материал и примеры решения задач Приведём основные приёмы решения уравнений в целых числах.
- Разложение на множители с последующим перебором возможных вариантов.
Пример оформления заказа №4.
Решить в натуральных числах уравнение 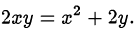
Решение:
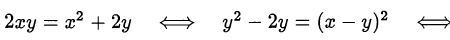
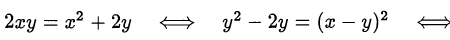
Следовательно, оба множителя равны единице и 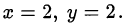
Ответ. (2;2).
Пример оформления заказа №5.
Решить в целых числах уравнение 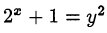 .
.
Решение:
Если 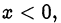 то
то 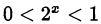 и
и 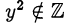 . При
. При 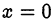 также
также 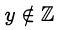 .
.
Пусть 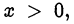 тогда
тогда 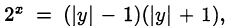 следовательно,
следовательно, 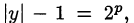
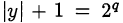 и
и 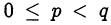 . Откуда
. Откуда
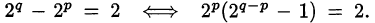
Возможные варианты:
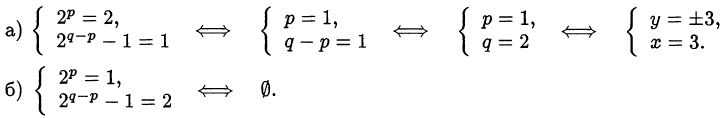
Ответ: (3;3), (3;-3).
• Использование делимости целых чисел.
Пример оформления заказа №6.
Доказать, что уравнение 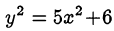 не имеет решений в целых числах.
не имеет решений в целых числах.
Решение:
Перепишем уравнение в виде
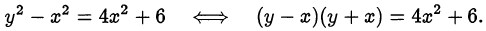
Так как правая часть уравнения является чётным числом, то и левая часть также должна быть чётным числом. Если 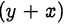 чётно, то
чётно, то 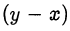 тоже чётно, и наоборот. Следовательно, левая часть уравнения делится на 4, но правая часть на 4 не делится. Значит уравнение не имеет решений.
тоже чётно, и наоборот. Следовательно, левая часть уравнения делится на 4, но правая часть на 4 не делится. Значит уравнение не имеет решений.
• Использование оценок с последующим перебором возможных значений.
Эта ссылка возможно вам будет полезна:
| Решение задач по математике |
Пример оформления заказа №7.
Решить в натуральных числах уравнение 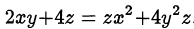 .
.
Решение:
Вынесем 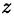 за скобки:
за скобки:
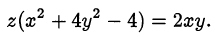
Выражение в скобках не равно нулю, так как иначе 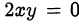 , что неверно при
, что неверно при 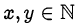 . Следовательно,
. Следовательно,
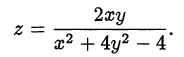
Так как 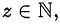 то
то 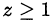 , то есть
, то есть
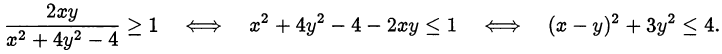
Откуда видно, что 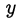 не может быть больше 1, а при
не может быть больше 1, а при 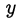 = 1 получаем
= 1 получаем
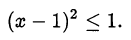
Следовательно, 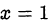 либо
либо 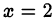 .
.
Ответ. (1; 1; 2), (2;1;1).
• Рассмотрение остатков.
Пример оформления заказа №8.
Решить в целых числах уравнение 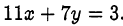
Решение:
Выразив 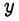 через
через 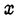 , получим
, получим 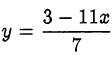 . Представим
. Представим 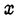 в виде
в виде
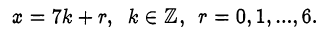
Тогда 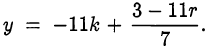 Для того, чтобы у было целым надо, чтобы
Для того, чтобы у было целым надо, чтобы 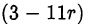 делилось на 7. В результате перебора всех значений
делилось на 7. В результате перебора всех значений 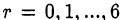 оказывается, что подходит только
оказывается, что подходит только 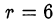 . Следовательно,
. Следовательно, 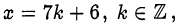
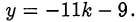
Ответ. 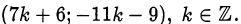
Смешанные задачи на целые числа
При решении смешанных задач пригодятся методы и приёмы решения задач на целые числа, приведённые в предыдущих разделах, а именно: разложение на множители с последующим перебором возможных вариантов, использование делимости целых чисел, рассмотрение остатков, использование оценок с последующим перебором возможных значений.
Также в этот раздел включены задачи, связанные с исследованием сократимости дробей вида 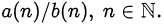 Существует несколько способов решения таких задач.
Существует несколько способов решения таких задач.
• Предполагается сократимость дроби на натуральное 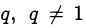 . Этот факт переписывается в виде двух равенств для числителя и знаменателя. Затем исключается исходная переменная
. Этот факт переписывается в виде двух равенств для числителя и знаменателя. Затем исключается исходная переменная 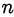 и получается равенство для
и получается равенство для 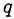 , из которого находятся возможные значения
, из которого находятся возможные значения 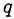 .
.
• Заданная дробь 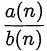 представляется в виде
представляется в виде
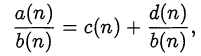
где выражения 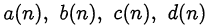 принимают целочисленные значения. Поскольку натуральное число к является общим делителем выражений
принимают целочисленные значения. Поскольку натуральное число к является общим делителем выражений 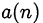 и
и 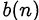 тогда и только тогда, когда оно является общим делителем выражений
тогда и только тогда, когда оно является общим делителем выражений 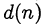 и
и 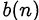 , вопрос о сократимости исходной дроби сводится к исследованию сократимости дроби
, вопрос о сократимости исходной дроби сводится к исследованию сократимости дроби 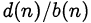 . В случаях, когда указанное представление исходной дроби является выделением целой части или когда
. В случаях, когда указанное представление исходной дроби является выделением целой части или когда 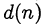 не зависит от
не зависит от 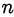 (то есть является целым числом), исследование сократимости новой дроби
(то есть является целым числом), исследование сократимости новой дроби 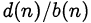 является, как правило, менее трудоёмким, чем исследование сократимости исходной дроби
является, как правило, менее трудоёмким, чем исследование сократимости исходной дроби 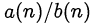 .
.
Напомним также, что если числа 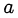 и
и 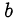 представлены в виде произведения простых множителей
представлены в виде произведения простых множителей
то наибольший общий делитель (НОД) и наименьшее общие кратное (НОК) этих чисел вычисляются следующим образом:
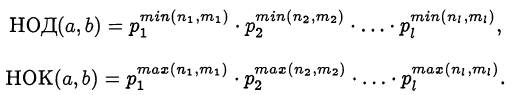
Замечание.
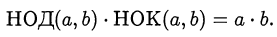
Пример оформления заказа №9.
При каких 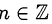 выражение
выражение 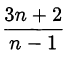 является целым числом:
является целым числом:
Решение:
Так как 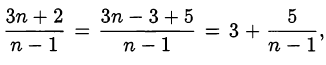 то исходное число будет целым только, если целым будет число
то исходное число будет целым только, если целым будет число 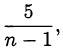 что возможно при
что возможно при 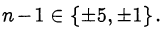
Ответ, 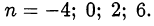
Пример оформления заказа №10.
Доказать, что дробь 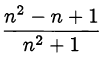 несократима ни при каком
несократима ни при каком 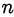 .
.
Решение:
Преобразуем исходную дробь
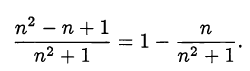
Если сократима дробь 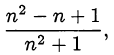 то сократима дробь
то сократима дробь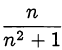 Если сократима дробь
Если сократима дробь 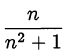 , то сократима дробь
, то сократима дробь 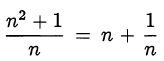 и сократима дробь
и сократима дробь 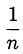 , что неверно. Следовательно, исходная дробь несократима.
, что неверно. Следовательно, исходная дробь несократима.
Пример оформления заказа №11.
При каких натуральных 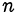 число
число 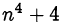 простое?
простое?
Решение:
Так как
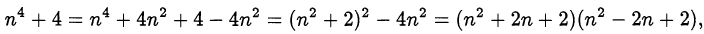
то 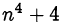 — простое число, только если
— простое число, только если 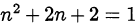 или
или  . Первое уравнение решений в натуральных числах не имеет. Решением второго уравнения является
. Первое уравнение решений в натуральных числах не имеет. Решением второго уравнения является 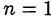 , в этом случае выражение
, в этом случае выражение 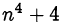 равно 5, то есть является простым числом.
равно 5, то есть является простым числом.
Ответ. 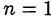 .
.
Пример оформления заказа №12.
Является ли полным квадратом число 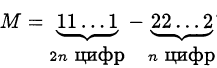 ?
?
Решение:
Так как
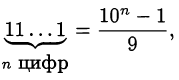
то
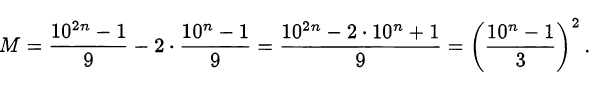
Так как 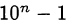 делится нацело на 3, то исходное число является полным квадратом.
делится нацело на 3, то исходное число является полным квадратом.
Ответ. Да.
Рациональные и иррациональные числа
Рациональным числом называется действительное число, представимое в виде несократимой дроби 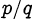 , где
, где 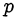 — целое число,
— целое число, 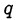 — натуральное число.
— натуральное число.
Иррациональным числом называется действительное число, непредставимое в виде несократимой дроби 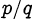 .
.
Замечание 1. Любое рациональное число можно представить в виде конечной десятичной дроби или бесконечной периодической десятичной дроби, а любое иррациональное число — в виде бесконечной непериодической десятичной дроби.
Замечание 2. Сумма, разность, произведение и частное двух рациональных чисел всегда является рациональным числом. Сумма, разность, произведение и частное двух иррациональных чисел может оказаться как рациональным, так и иррациональным числом.
Доказательство иррациональности числа, как правило, проводится от противного. Предполагается, что заданное число можно представить в виде несократимой дроби, после чего полученное равенство с помощью алгебраических преобразований приводится к уравнению в целых числах, не имеющему решений.
Утверждение 1. Если числа 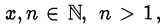 а
а 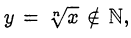 , то
, то 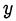 — иррационально.
— иррационально.
Доказательство. Предположим противное. Пусть 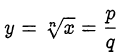 — несократимая дробь, тогда
— несократимая дробь, тогда 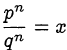 . Пусть
. Пусть 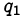 — делитель числа
— делитель числа 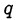 и
и 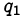 — простое число. Так как
— простое число. Так как 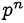 делится на
делится на 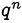 , то
, то 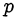 делится на
делится на 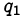 . Следовательно, дробь
. Следовательно, дробь 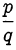 сократима на
сократима на 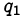 , а это противоречит нашему предположению. Значит,
, а это противоречит нашему предположению. Значит, 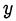 — иррационально.
— иррационально.
Утверждение 2. Если 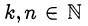 взаимно простые числа и
взаимно простые числа и 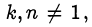 то
то 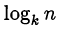 -число иррациональное.
-число иррациональное.
Доказательство. Предположим противное. Пусть 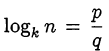 — несократимая дробь, тогда
— несократимая дробь, тогда 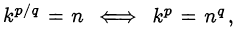 , что невозможно, так как у
, что невозможно, так как у 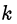 и
и 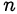 нет общих делителей.
нет общих делителей.
Пример оформления заказа №13.
Доказать иррациональность числа 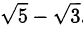
Решение:
Пусть 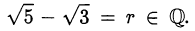 . Тогда
. Тогда 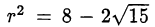 и, следовательно,
и, следовательно, 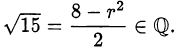 . Но
. Но 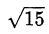 иррационально согласно утверждению 1. Значит наше предположение о том, что
иррационально согласно утверждению 1. Значит наше предположение о том, что 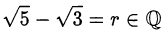 — неверно.
— неверно.
Пример оформления заказа №14.
Доказать, что число 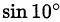 иррационально.
иррационально.
Решение:
Из формулы синуса тройного угла получим

Предположим, что 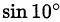 — рациональное число, то есть
— рациональное число, то есть 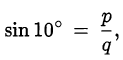 где
где 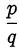 — несократимая дробь. Тогда
— несократимая дробь. Тогда

Из последнего равенства следует, что 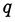 — чётное, то есть
— чётное, то есть 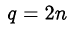 . Тогда
. Тогда

Следовательно, 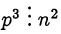 , а так как дробь
, а так как дробь 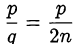 несократима, то
несократима, то 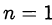 . Поскольку полученное в этом случае уравнение для
. Поскольку полученное в этом случае уравнение для 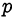

решений в целых числах не имеет, число 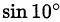 нельзя представить в виде несократимой дроби
нельзя представить в виде несократимой дроби 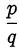 и, значит, оно является иррациональным.
и, значит, оно является иррациональным.
Пример оформления заказа №15.
Доказать, что число 0,1010010001… является иррациональным.
Решение:
Пусть оно рациональное. Тогда в его десятичной записи есть период из 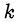 цифр. Но в записи числа сколь угодно далеко от начала встречаются
цифр. Но в записи числа сколь угодно далеко от начала встречаются 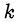 нулей подряд. Следовательно, в периоде содержатся одни нули, а это противоречит условию.
нулей подряд. Следовательно, в периоде содержатся одни нули, а это противоречит условию.
Сравнение чисел
При решении задач этого раздела будут полезными следующие приёмы.
- В случае сравнения однотипных числовых выражений следует алгебраическими преобразованиями привести исходную задачу к сравнению двух целых чисел.
- При сравнении разнотипных числовых выражений
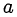 и
и 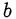 подбирают такое число
подбирают такое число 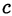 , которое сравнимо и
, которое сравнимо и 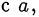 и
и 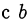 . Например, для обоснования неравенства
. Например, для обоснования неравенства 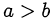 находят число с такое, что
находят число с такое, что 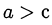 и
и 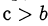 .
. - Иногда бывает удобно ввести некоторую вспомогательную функцию
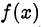 и заменить исходную задачу сравнения на сравнение значений функции
и заменить исходную задачу сравнения на сравнение значений функции 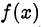 при заданных значениях аргумента.
при заданных значениях аргумента.
Также могут оказаться полезными следующие неравенства:
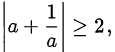 где
где 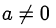 (оценка суммы двух взаимно обратных величин), равенство достигается при
(оценка суммы двух взаимно обратных величин), равенство достигается при 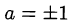 ;
;
• 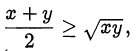 , где
, где 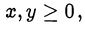 равенство достигается при
равенство достигается при 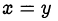 (среднее геометрическое не превосходит среднего арифметического);
(среднее геометрическое не превосходит среднего арифметического);
• 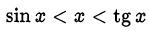 при
при 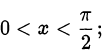
• 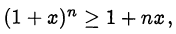 где
где 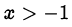 и
и 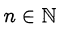 (неравенство Бернулли).
(неравенство Бернулли).
При сравнении логарифмов может быть полезным следующее утверждение. Утверждение 1. 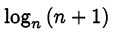 при
при 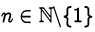 убывает с ростом
убывает с ростом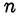 . Доказательство. Представим
. Доказательство. Представим 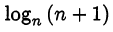 в виде
в виде
logn (n + 1) = log,
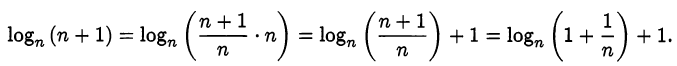
Для строгого доказательства убывания первого слагаемого достаточно записать его в виде дроби
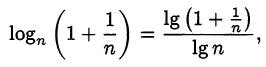
где числитель убывает, а знаменатель возрастает. Таким образом, первое слагаемое убывает, а, следовательно, убывает и сумма. Что и требовалось доказать.
Пример оформления заказа №16.
Что больше: 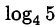 или
или 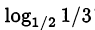 ?
?
Решение:
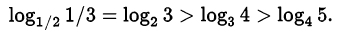 .
.
Ответ. 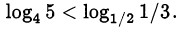
Пример оформления заказа №17.
Сравнить числа 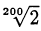 и 1,006.
и 1,006.
Решение:
Составим формальное неравенство и возведём обе его части в степень 200:
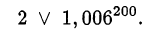
Оценим правую часть с помощью неравенства Бернулли:
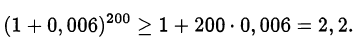
То есть 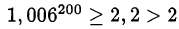 и, следовательно,
и, следовательно, 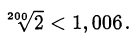
Ответ. 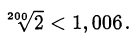
Пример оформления заказа №18.
Что больше: 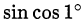 или
или 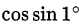 ?
?
Решение:
Покажем, что
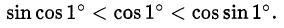
1) Неравенство 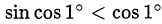 следует из того, что в первой четверти
следует из того, что в первой четверти 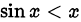 .
.
2) Неравенство 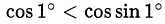 выполняется потому, что
выполняется потому, что 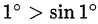 , а в первой четверти
, а в первой четверти  убывает.
убывает.
Ответ, 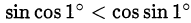 .
.
Замечание. Неравенство 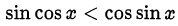 справедливо при всех
справедливо при всех 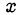 .
.
Пример оформления заказа №19.
Сравнить числа 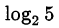 и
и 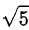 .
.
Решение:
Оба числа (проверьте самостоятельно) лежат на отрезке [2; 3]. Сравним их с серединой отрезка, то есть с 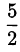 :
:
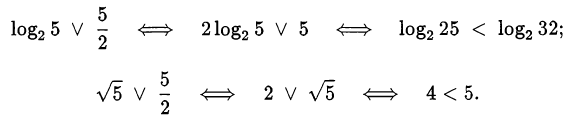
Следовательно, числа 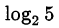 и
и 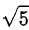 лежат на отрезке
лежат на отрезке 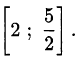 Сравним их с серединой этого отрезка, то есть
Сравним их с серединой этого отрезка, то есть 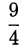 :
:

Следовательно, 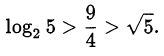
Ответ. 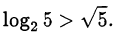
Пример оформления заказа №20.
Доказать, что 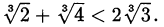 .
.
Решение:
Возведём обе части неравенства в куб:
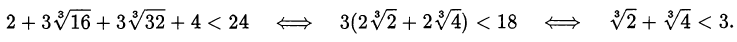
Обозначим 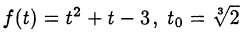 и покажем, что
и покажем, что 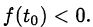
Неравенство 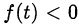 справедливо при
справедливо при 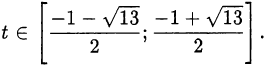 Докажем, что
Докажем, что
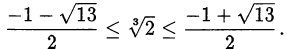
Поскольку 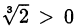 , левое неравенства очевидно. Правое неравенство равносильно неравенству
, левое неравенства очевидно. Правое неравенство равносильно неравенству  . Возведём обе части в куб:
. Возведём обе части в куб:

так как после возведения в квадрат получим очевидное неравенство 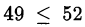 . Следовательно, исходное неравенство также справедливо.
. Следовательно, исходное неравенство также справедливо.
Тригонометрические неравенства, обратные тригонометрические функции
Основные свойства арксинуса, арккосинуса, арктангенса и арккотангенса. Преобразование выражений с обратными тригонометрическими функциями
В этом разделе собраны задачи, связанные с преобразованием выражений, содержащих обратные тригонометрические функции. Для решения таких задач достаточно знать определения обратных тригонометрических функций и помнить основные тригонометрические формулы:
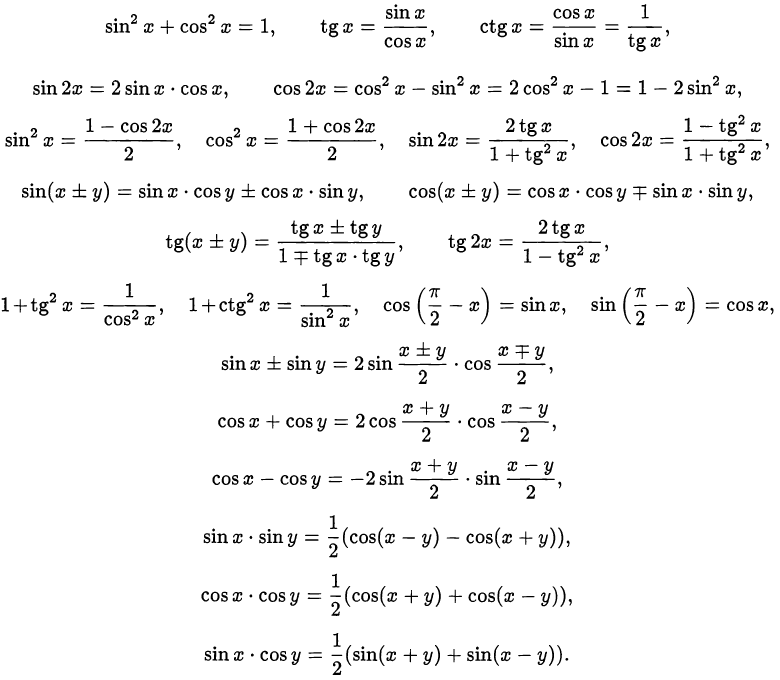
He забывайте, что тригонометрические формулы справедливы лишь при соответствующих допустимых значениях аргументов.
Напомним определения обратных тригонометрических функций:
• арксинусом числа 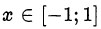 называется число
называется число 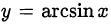 , удовлетворяющее двум условиям:
, удовлетворяющее двум условиям: 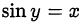 и
и 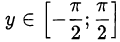 ;
;
• арккосинусом числа 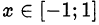 называется число
называется число 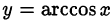 , удовлетворяющее двум условиям:
, удовлетворяющее двум условиям: 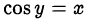 и
и 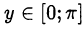 ;
;
• арктангенсом числа 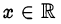 называется число
называется число 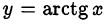 , удовлетворяющее двум условиям:
, удовлетворяющее двум условиям: 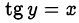 и
и 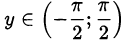 ;
;
• арккотангенсом числа 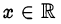 называется число
называется число 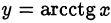 , удовлетворяющее двум условиям:
, удовлетворяющее двум условиям: 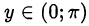 и
и 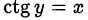 .
.
График обратной тригонометрической функции симметричен графику основной тригонометрической функции относительно прямой 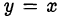 на соответствующей области определения:
на соответствующей области определения:
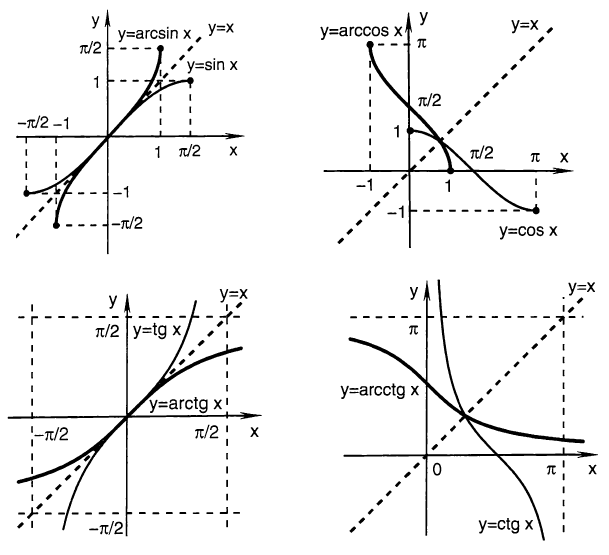
Полезно также знать следующие формулы, связанные с обратными тригонометрическими функциями:
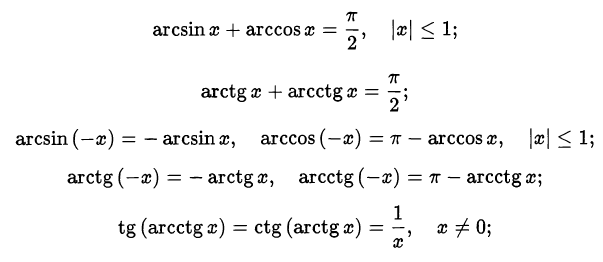
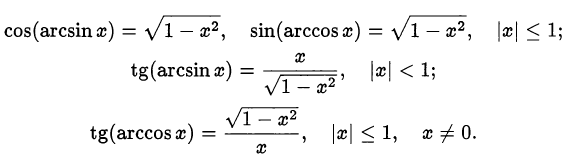
Подобные формулы получаются при комбинировании определений обратных тригонометрических функций и основных тригонометрических формул.
Пример оформления заказа №21.
Докажем формулу:
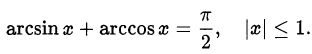
Доказательство. Перепишем исходное равенство в виде
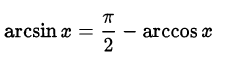
и докажем его, используя определение арксинуса. Проверим выполнение двух условий:
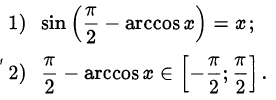
С помощью формулы приведения получаем, что
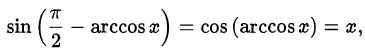
следовательно, первое условие выполняется. Проверим выполнение второго условия:
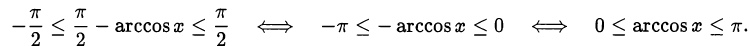
Справедливость последнего неравенства следует из определения арккосинуса.
Пример оформления заказа №22.
Вычислить
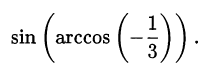
Решение:
Положим 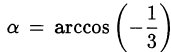 , тогда
, тогда 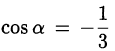 и
и 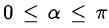 . Из основного тригонометрического тождества следует, что
. Из основного тригонометрического тождества следует, что
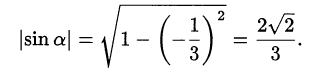
Так как 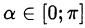 , то подходит только положительное значение синуса.
, то подходит только положительное значение синуса.
Замечание. Аналогичным образом доказываются и другие формулы этого раздела в общем случае.
Ответ: 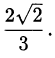
Пример оформления заказа №23.
Построить график функции 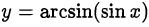 .
.
Решение:
Так как 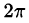 является периодом функции
является периодом функции 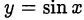 , то
, то 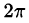 будет периодом и для функции
будет периодом и для функции 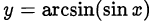 . Поэтому нам достаточно построить график этой функции на отрезке
. Поэтому нам достаточно построить график этой функции на отрезке 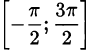 , а потом продолжить его на всю числовую ось этой функции на отрезке с учётом периодичности.
, а потом продолжить его на всю числовую ось этой функции на отрезке с учётом периодичности.
1) Рассмотрим отрезок 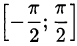 :
:
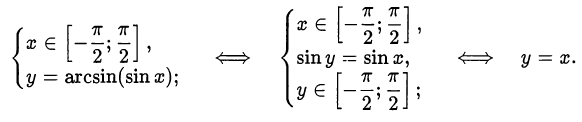
2) На отрезке 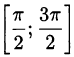 получим
получим
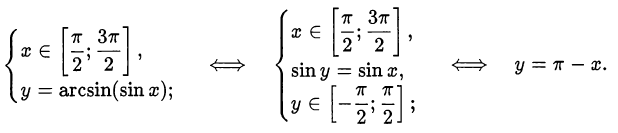
3) Продолжим график с учётом периодичности на всю числовую прямую.
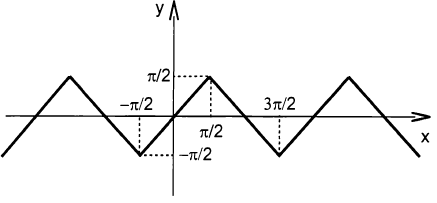
Замечание. Аналогичным образом строятся графики функций
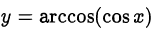
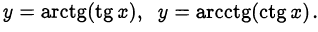
Уравнения и неравенства с обратными тригонометрическими функциями
Для успешного решения уравнений и неравенств с обратными тригонометрическими функциями достаточно знать определения и свойства обратных тригонометрических функций.
Напомним, что функции 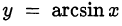 и
и 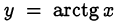 монотонно возрастают на своих областях определения и принимают значения из промежутков
монотонно возрастают на своих областях определения и принимают значения из промежутков 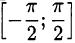 и
и 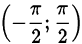 соответственно, а функции
соответственно, а функции 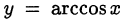 и
и 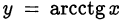 монотонно убывают на своих областях определения и принимают значения из промежутков
монотонно убывают на своих областях определения и принимают значения из промежутков 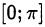 и
и 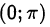 соответственно.
соответственно.
Общий метод решения задач с обратными тригонометрическими функциями состоит в применении одной и той же тригонометрической функции к обеим частям данного уравнения или неравенства. При этом для обеспечения равносильности переходов необходимо тщательно следить за областью значений левой и правой частей исходного уравнения (неравенства), при необходимости рассматривая задачу на нескольких промежутках.
Пример оформления заказа №24.
Решить неравенство
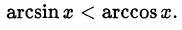
Решение:
Применив формулу
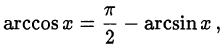
получим
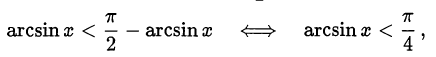
откуда в силу монотонности арксинуса следует, что 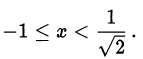
Ответ. 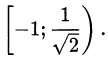
Пример оформления заказа №25.
Решить уравнение
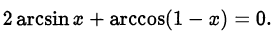
Решение:
Первый способ. Перепишем уравнение в виде
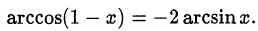
Согласно определению арккосинуса это равенство равносильно системе
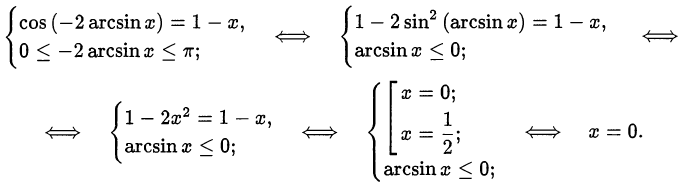
Второй способ. Проанализируем, в каких пределах может изменяться переменная 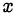 . Обратные тригонометрические функции, входящие в исходное уравнение
. Обратные тригонометрические функции, входящие в исходное уравнение
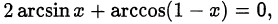
определены при
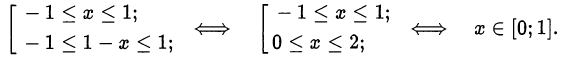
При этих значениях переменной 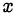 оба слагаемых исходного уравнения неотрицательны, и равенство нулю возможно только в случае
оба слагаемых исходного уравнения неотрицательны, и равенство нулю возможно только в случае
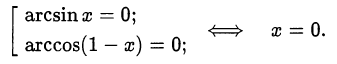
Ответ. 0.
Пример оформления заказа №26.
Решить уравнение
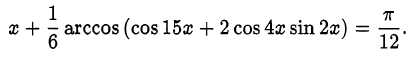
Решение:
Перепишем уравнение в виде
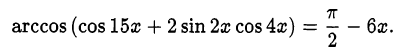
Согласно определению арккосинуса это равенство равносильно системе
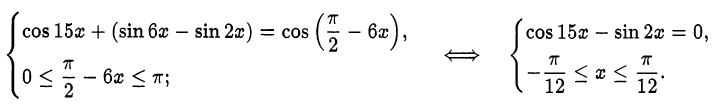
Используя формулу приведения, решим уравнение:
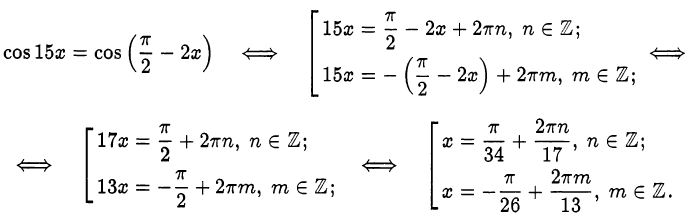
Осталось произвести отбор корней по условию 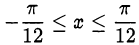 .
.
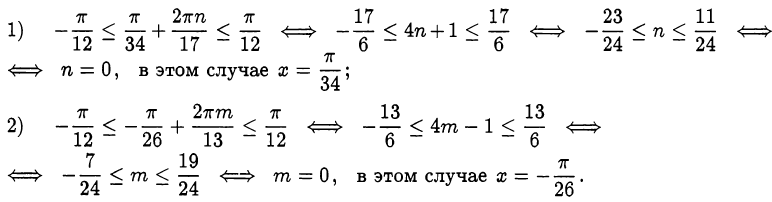
Ответ. 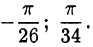
Отбор решений в тригонометрических уравнениях. Тригонометрические неравенства
Тригонометрические неравенства нередко возникают при решении уравнений, содержащих наряду с тригонометрическими функциями радикалы и логарифмы. Если тригонометрическое неравенство возникает как дополнительное ограничение при решении уравнения, то в большинстве задач удобнее сначала решить уравнение, а затем произвести отбор полученных корней посредством подстановки в неравенство.
Если необходимость в решении тригонометрического неравенства остаётся, советуем воспользоваться тригонометрической окружностью. И хотя способы решения тригонометрических неравенств тесно переплетаются со способами решения соответствующих тригонометрических уравнений, графическая иллюстрация поможет избежать ошибок при отборе.
Пример оформления заказа №27.
Решить неравенство
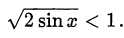
Решение:
Исходное неравенство равносильно следующему двойному неравенству:
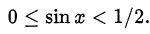
Отметим на тригонометрической окружности углы, синусы которых удовлетворяют этому условию.
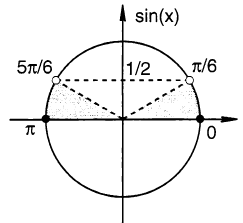
Получим промежутки
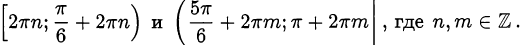
Ответ.
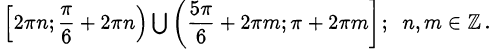
Пример оформления заказа №28.
Найти все решения уравнения
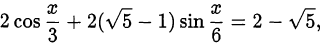
удовлетворяющие условию 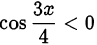 .
.
Решение:
С помощью формулы косинуса двойного утла уравнение сводится к квадратному:
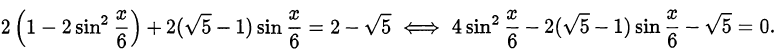
Корень 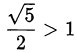 не подходит. Второй корень равен
не подходит. Второй корень равен 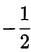 ; следовательно,
; следовательно,
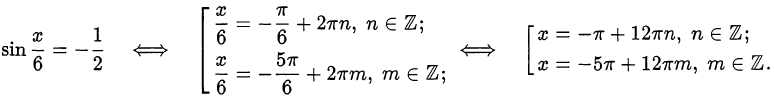
Отберём те значения переменной, для которых выполняется условие 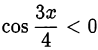 .
.
1)- Если
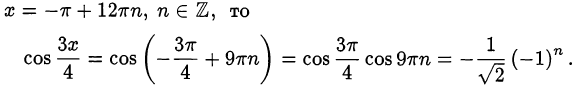
Значение косинуса отрицательно при чётном 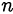 . Следовательно,
. Следовательно, 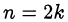 и, значит,
и, значит,
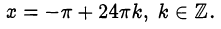
2) Если
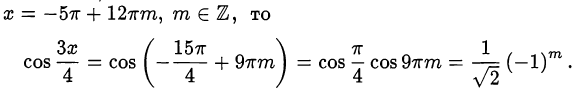
Косинус отрицателен при нечётном 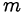 . Следовательно,
. Следовательно, 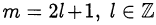 и, значит,
и, значит,
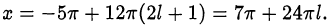
Ответ.
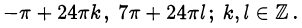
Пример оформления заказа №29.
Решить уравнение
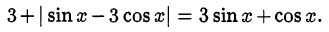
Решение:
Разделим обе части уравнения на 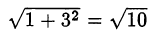 и введём вспомогательный аргумент
и введём вспомогательный аргумент 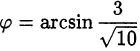 :
:
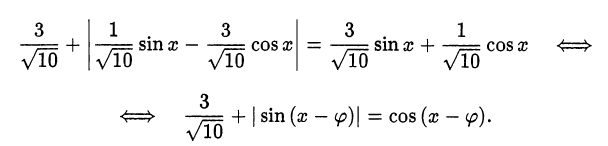
Обозначим
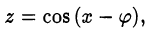
тогда уравнение примет вид:
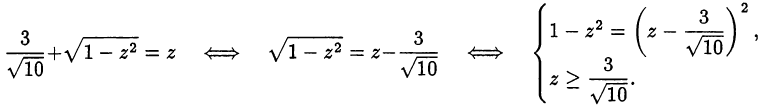
Уравнение системы сводится к квадратному уравнению 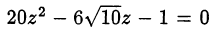 имеет корни
имеет корни 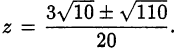 . Заметим, что из первой строки системы следует неотрицательность выражения
. Заметим, что из первой строки системы следует неотрицательность выражения 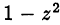 ; следовательно, оба корня удовлетворяют условию
; следовательно, оба корня удовлетворяют условию 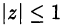 .
.
Сравним оба корня с числом 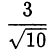 .
.
1) 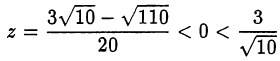 — не подходит.
— не подходит.
2) Сравним второй корень:
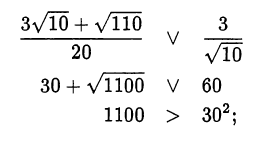
значит,
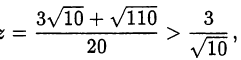
и это значение нам подходит. В результате
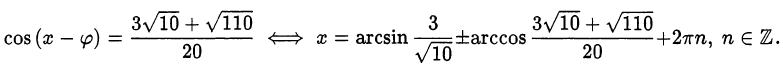
Ответ,
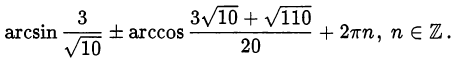
Полезные преобразования и замены переменных
Использование формул сокращённого умножения, выделение полного квадрата
В этом параграфе собраны задачи, при решении которых используются различные полезные формулы и преобразования: формулы сокращённого умножения, теорема Везу, выделение полного квадрата, домножение на сопряжённое выражение, введение новых переменных.
Напомним базовые формулы сокращённого умножения:
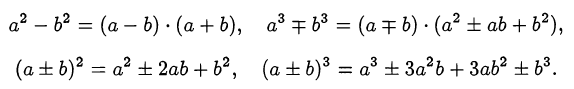
Для поиска рациональных корней уравнений высших степеней с целыми коэффициентами удобно пользоваться следующей теоремой.
Теорема Безу. Если уравнение

с целыми коэффициентами 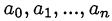 имеет рациональные корни, то есть корни, представимые в виде несократимой дроби
имеет рациональные корни, то есть корни, представимые в виде несократимой дроби 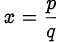 , то старший коэффициент
, то старший коэффициент 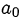 делится нацело на
делится нацело на 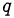 , а свободный член
, а свободный член 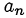 делится нацело на
делится нацело на 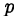 .
.
Следствие 1. Если уравнение имеет целые коэффициенты и старший из них равен единице, то рациональными корнями такого уравнения могут быть только целые числа.
Следствие 2. Целые корни уравнения с целыми коэффициентами являются делителями свободного члена.
Теорема Безу формулирует необходимое (но не достаточное) условие существования рациональных корней уравнений с целыми коэффициентами и является эффективным инструментом разложения на множители многочленов высших степеней.
Для получения более чёткого представления о структуре выражения полезно вводить новые переменные (одну или несколько). На возможность использования таких замен обычно указывает наличие повторяющихся выражений в уравнении или неравенстве.
Во многих задачах с параметрами полезно сначала выяснить, какая из переменных является параметром по существу условия, а какая — независимой переменной. Иногда по смыслу задачи 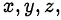 … играют роль параметров, в то время как
… играют роль параметров, в то время как 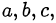 … играют роль переменных.
… играют роль переменных.
Напоминаем вам, что после решения задачи в новых переменных необходимо возвращаться к исходным переменным.
Пример оформления заказа №30.
Решить систему уравнений
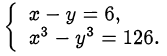
Решение:
Преобразуем второе уравнение системы, используя формулу разности кубов:
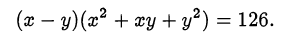
Далее выделим полный квадрат во втором сомножителе левой части преобразованного уравнения:
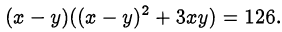
Подставим значение 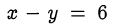 из первого уравнения, тогда второе уравнение принимает следующий вид:
из первого уравнения, тогда второе уравнение принимает следующий вид:
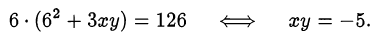
Получаем систему уравнений, эквивалентную исходной:

Подставляя найденные значения переменной 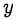 в первое уравнение системы, находим соответствующие им значения переменной
в первое уравнение системы, находим соответствующие им значения переменной 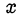 .
.
Ответ. (1; -5), (5; -1).
Пример оформления заказа №31.
Вычислить
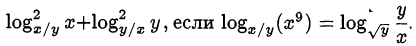
Решение:
Обозначим искомое выражение через 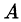 и преобразуем его.
и преобразуем его.
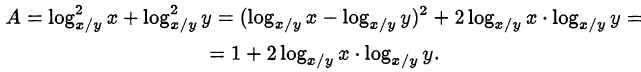
Из условия получаем:

Значит,
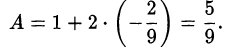
Ответ. 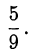
Пример оформления заказа №32.
Найти наименьшее значение произведения 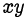 , где
, где 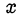 и
и 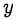 удовлетворяют системе
удовлетворяют системе
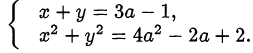
Решение:
Заметим, что
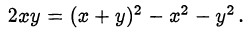
Возведём обе части первого уравнения в квадрат и почленно вычтем из них обе части второго уравнения:
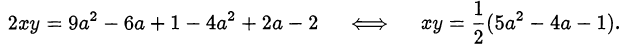
Для того чтобы найти наименьшее значение, которое может принимать произведение 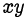 , надо найти минимум квадратичной функции
, надо найти минимум квадратичной функции
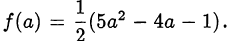
График функции 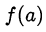 — парабола, ветви которой направлены вверх. Минимальное значение функция принимает в точке
— парабола, ветви которой направлены вверх. Минимальное значение функция принимает в точке 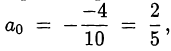 , которая является абсциссой вершины параболы. Значение функции в этой точке
, которая является абсциссой вершины параболы. Значение функции в этой точке 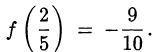
Таким образом, минимальное значение, которое может принимать произведение 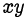 — это значение —
— это значение — 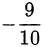 . Осталось убедиться, что при
. Осталось убедиться, что при 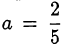 исходная система имеет решение. При
исходная система имеет решение. При 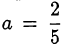 система принимает вид
система принимает вид
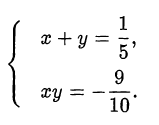
Решая систему подстановкой, приходим к уравнению
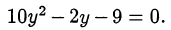
Вычислим дискриминант:
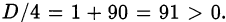
Из положительности дискриминанта заключаем, что решение системы существует; следовательно, минимальное значение 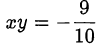 достигается.
достигается.
Ответ. 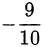 .
.
Пример оформления заказа №33.
Найти все значения 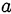 , при которых неравенство
, при которых неравенство
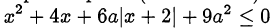
имеет не более одного решения.
Решение:
Преобразуем исходное неравенство:

Последнее двойное неравенство имеет не более одного решения тогда и только тогда, когда 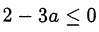 , то есть
, то есть 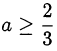 .
.
Ответ. 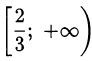 .
.
Замены переменных в рациональных уравнениях, неравенствах и системах
Перечислим основные ситуации, в которых целесообразно использовать замену:
- наличие повторяющегося выражения;
- возможность приведения к симметричному виду, например, уравнение
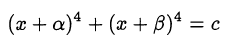
после замены
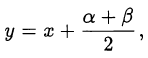
приводится к биквадратному уравнению
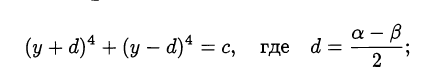
• «возвратность» уравнения, например, уравнение
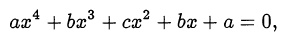
после деления на 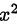 , преобразуется к уравнению
, преобразуется к уравнению
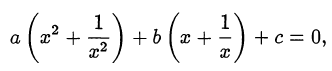
квадратному относительно
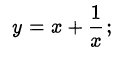
«однородность» уравнения, например, уравнение
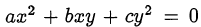
при 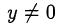 равносильно квадратному уравнению
равносильно квадратному уравнению
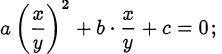
• «симметричность» уравнений системы, например, при решении системы
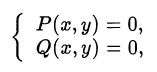
где
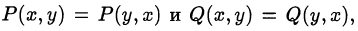
замена
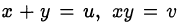
может упростить вычисления.
Эта ссылка возможно вам будет полезна:
| Помощь по математике |
Пример оформления заказа №34.
Решить систему
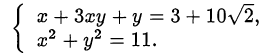
Решение:
Перепишем систему в виде
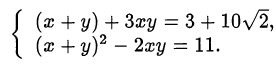
Сделаем замену переменных
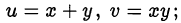
тогда

Подставив выражение для 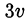 из первого уравнения во второе, получим квадратное уравнение относительно
из первого уравнения во второе, получим квадратное уравнение относительно 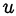 :
:
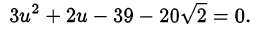
Решим это уравнение:
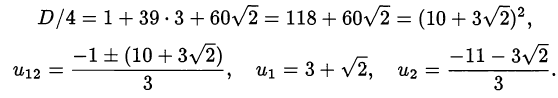
Из первого уравнения последней системы определяем 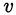 :
:
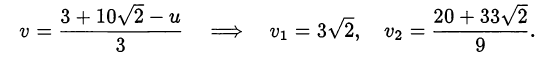
Возвращаясь к исходным переменным, получим две системы уравнений для нахождения 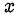 и
и 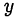 :
:
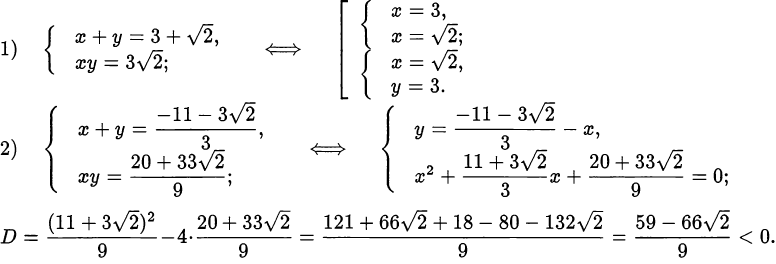
Значит, во втором случае решений нет.
Ответ. 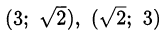 .
.
Пример оформления заказа №35.
Решить уравнение
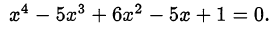
Решение:
Так как 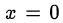 не является решением нашего уравнения, то можем поделить его на
не является решением нашего уравнения, то можем поделить его на 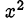 . Получим
. Получим
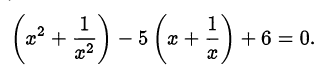
Положим
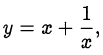
тогда
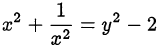
и уравнение примет вид:

Ответ. 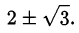
Пример оформления заказа №36.
Решить систему уравнений

Решение:
Умножим первое уравнение системы на 6, второе уравнение — на 11 и приравняем левые части полученных уравнений:
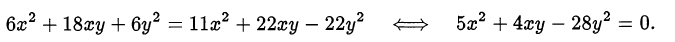
Заметим, что, если 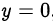 , то исходная система не имеет решений. Разделим однородное уравнение на
, то исходная система не имеет решений. Разделим однородное уравнение на 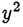 и сделаем замену
и сделаем замену 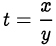 , получим
, получим
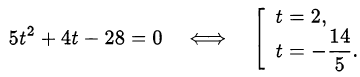
Первый случай:
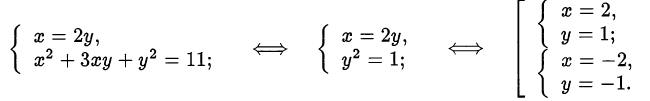
Второй случай:
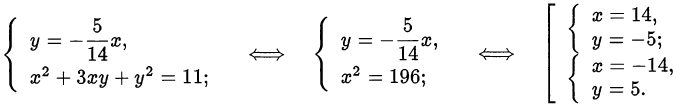
Ответ. (2; 1), (-2;-1), (14;-5), (-14;5).
Замены переменных в иррациональных уравнениях, неравенствах и системах
В некоторых задачах целесообразно заменить иррациональное выражение на новую переменную так, чтобы уравнение или неравенство приняло существенно более простой вид. Иногда удачная замена позволяет выделить полный квадрат некоторого выражения под арифметическим квадратным корнем (этот метод рассмотрен в примере 3).
Кроме того, полезно вводить ограничения для введённых новых переменных, которые определяются их областью значений. Например, при замене 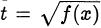 появляется очевидное ограничение
появляется очевидное ограничение 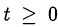 . Такие ограничения помогают производить отбор допустимых значений новых переменных и избегать рассмотрения случаев, приводящих к уравнениям или неравенствам с пустым множеством решений.
. Такие ограничения помогают производить отбор допустимых значений новых переменных и избегать рассмотрения случаев, приводящих к уравнениям или неравенствам с пустым множеством решений.
Пример оформления заказа №37.
Решить уравнение
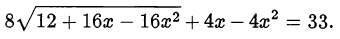
Решение:
Добавим 3 к обеим частям уравнения и вынесем множитель 4 из подкоренного выражения:
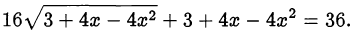
Пусть 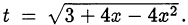 Заметим, что новая переменная
Заметим, что новая переменная 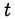 может принимать только неотрицательные значения. Исходное уравнение преобразуется к квадратному относительно
может принимать только неотрицательные значения. Исходное уравнение преобразуется к квадратному относительно 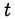 :
:

Значение 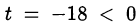 не подходит. Остаётся корень
не подходит. Остаётся корень 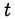 = 2. Возвращаемся к исходной переменной:
= 2. Возвращаемся к исходной переменной:
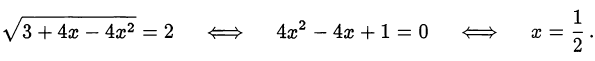
Ответ. 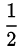 .
.
Пример оформления заказа №38.
Решить неравенство
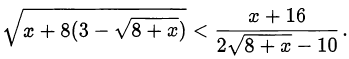
Решение:
Сделаем замену
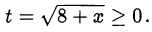
Исходное неравенство примет вид
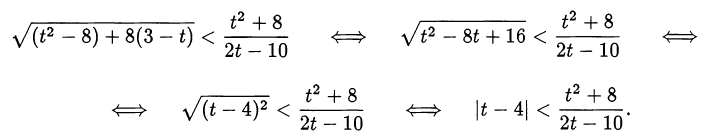
Так как правая часть последнего неравенства должна быть положительна, то
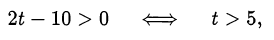
и, значит,
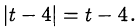
Приходим к системе
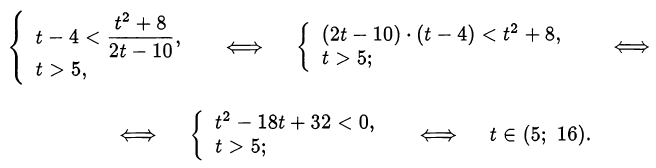
Вернёмся к переменной 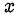 :
:
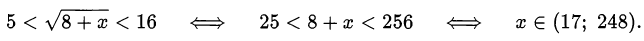
Ответ. (17;248).
Пример оформления заказа №39.
Решить уравнение
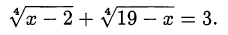
Решение:
Приведём два способа решения этой задачи.
1-й способ.
Левая часть уравнения определена тогда и только тогда, когда подкоренные выражения неотрицательны. Значит, 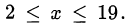 Возводя обе части уравнения в квадрат, получим
Возводя обе части уравнения в квадрат, получим
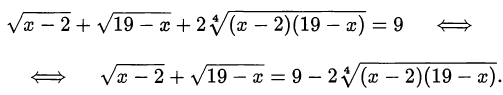
Уравнение имеет смысл при
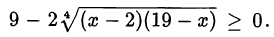
Возведём обе уравнения в квадрат:
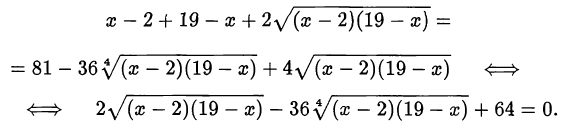
Сделаем замену
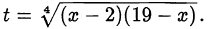
Получим систему относительно 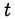 :
:
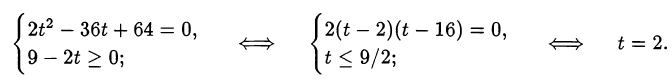
Возвращаемся к исходной переменной:
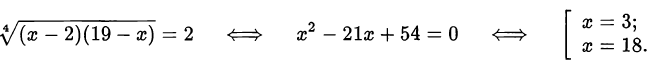
2-й способ.
Сделаем замену
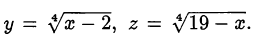
Тогда вместо уравнения получим систему
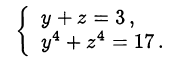
Преобразуем левую часть второго уравнения системы:
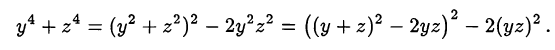
Подставим из первого уравнения системы значение суммы 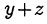 в преобразованное второе уравнение:
в преобразованное второе уравнение:
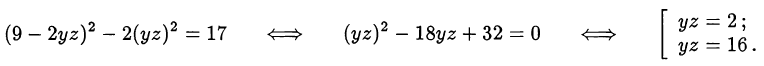
Таким образом, получаем две системы:

Решая их и возвращаясь к переменной 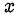 , находим
, находим
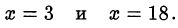
Ответ. 3; 18.
Замены переменных в показательных и логарифмических уравнениях, неравенствах и системах
В задачах, содержащих выражения с показательными и логарифмическими функциями, также целесообразно применять замены переменных.
Как правило, прежде чем производить замену, необходимо произвести некоторые преобразования степеней и логарифмов: привести все степенные функции к одному основанию (пример 2), перейти к логарифмам по одному основанию и с одинаковыми подлогарифменными функциями (примеры 1 и 3) и так далее.
При решении задач в новых переменных следует учитывать области значений заменённых выражений, чтобы отбросить полученные значения новых переменных, которые не удовлетворяют ограничениям, и тем самым сократить количество рассматриваемых случаев.
Пример оформления заказа №40.
Решить уравнение
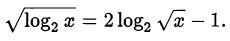
Решение:
Перепишем уравнение в виде

Сделаем замену переменной
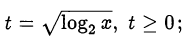
в новых обозначениях уравнение становится квадратным:

Принимая во внимание ограничение 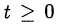 , отбрасываем отрицательный корень
, отбрасываем отрицательный корень 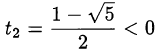 .
.
Возвращаемся к исходной переменной:

Ответ. 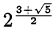 .
.
Пример оформления заказа №41.
Решить уравнение
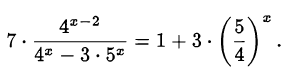
Решение:
Так как 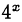 > 0, то можно поделить числитель и знаменатель левой части на
> 0, то можно поделить числитель и знаменатель левой части на 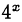 . Получим уравнение
. Получим уравнение
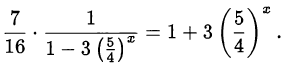
Сделаем замену переменной
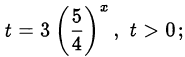
в новых обозначениях уравнение примет вид
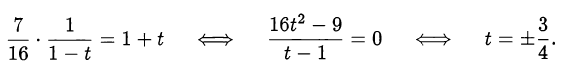
Поскольку 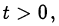 оставляем решение
оставляем решение 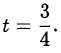 Возвращаемся к исходной переменной:
Возвращаемся к исходной переменной:

Ответ. 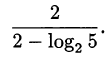
Пример оформления заказа №42.
Решить неравенство
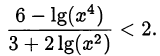
Решение:
Перепишем неравенство в виде 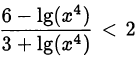 и сделаем замену
и сделаем замену 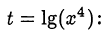
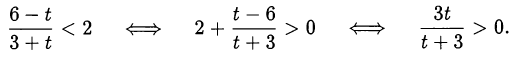
Последнее неравенство выполнено при 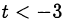 и
и 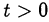 . Возвращаемся к исходной переменной:
. Возвращаемся к исходной переменной:
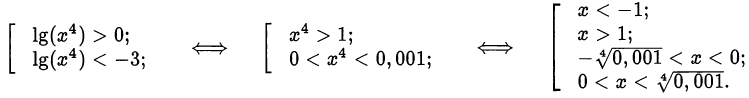
Ответ,
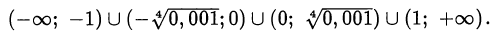
Пример оформления заказа №43.
Решить систему уравнений
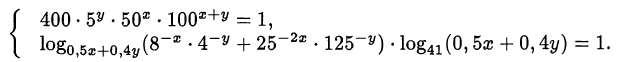
Решение:
Из второго уравнения следует, что
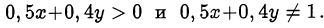
Преобразуем первое уравнение системы:
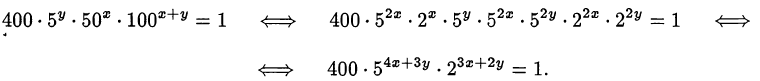
Преобразуем второе уравнение системы:
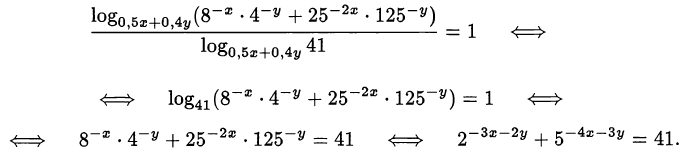
Сделаем замену переменных 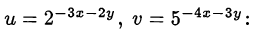
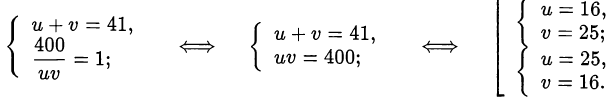
Вернёмся к исходным переменным. Рассмотрим первую пару 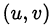 .
.
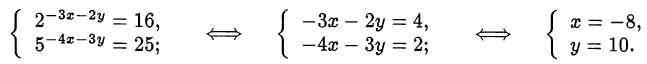
При полученных значениях 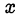 и
и 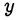 второе уравнение исходной системы не имеет смысла, так как основание логарифма в левой части равно нулю:
второе уравнение исходной системы не имеет смысла, так как основание логарифма в левой части равно нулю:
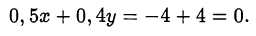
Рассмотрим вторую пару 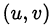 .
.
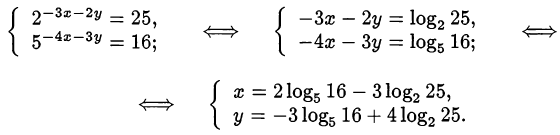
Проверим, имеет ли исходная система смысл при полученных значениях 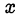 и
и 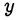 . Вычислим значение основания логарифма:
. Вычислим значение основания логарифма:
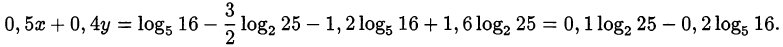
Сравним с нулём:
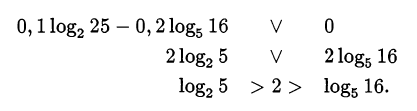
Значит, 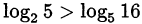 то есть основание логарифма положительно. Сравним его значение с единицей:
то есть основание логарифма положительно. Сравним его значение с единицей:
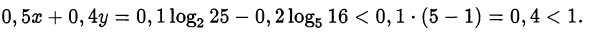
Итак, полученные значения 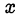 и
и 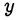 удовлетворяют исходной системе.
удовлетворяют исходной системе.
Ответ.
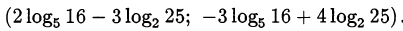
Замены в тригонометрических уравнениях и тригонометрические замены
В некоторых задачах удобно использовать следствия из основного тригонометрического тождества, например,
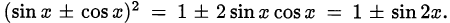
Другими словами, если тригонометрическое уравнение или неравенство содержит выражения вида 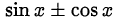 и
и 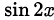 , то заменой переменных
, то заменой переменных 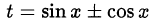 оно может быть сведено к алгебраическому (этот подход реализован в примере 1).
оно может быть сведено к алгебраическому (этот подход реализован в примере 1).
Если ОДЗ исходной задачи ограничена (например, уравнение содержит иррациональность вида 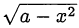 , поэтому область определения будет содержаться в отрезке
, поэтому область определения будет содержаться в отрезке 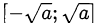 ), то можно сделать тригонометрическую замену переменной
), то можно сделать тригонометрическую замену переменной
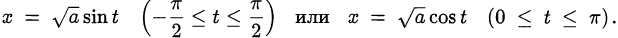
Такая замена в алгебраической задаче не приводит к потере возможных решений в силу ограниченности ОДЗ, но может существенно облегчить её решение благодаря большому арсеналу тригонометрических тождеств и способов преобразований тригонометрических выражений (см. пример 2).
Переход от алгебраической постановки к тригонометрической целесообразен и в случае, когда одно из уравнений задачи имеет вид
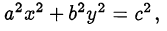
где 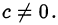
Приведя уравнение к виду
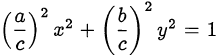
и сделав замену переменных
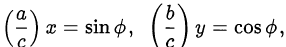
можно трактовать его как основное тригонометрическое тождество и смело переходить к тригонометрической интерпретации задачи в целом.
Пример оформления заказа №44.
Решить уравнение
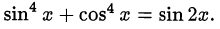
Решение:
Заметим, что
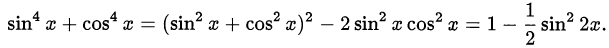
Сделаем замену переменной 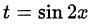 , при этом
, при этом 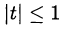 . Получим:
. Получим:

Решая последнее уравнение, с учётом условия на 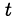 находим
находим 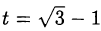 . Возвращаемся к переменной
. Возвращаемся к переменной 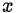 :
:
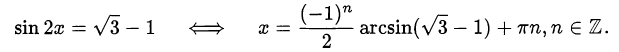
Ответ.
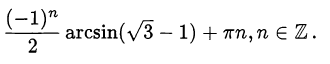
Пример оформления заказа №45.
Решить уравнение
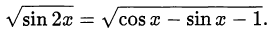
Решение:
Исходное уравнение эквивалентно системе
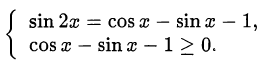
Учитывая, что 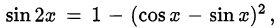 и заменяя
и заменяя 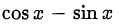 ; на новую переменную
; на новую переменную 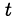 , перепишем систему в виде
, перепишем систему в виде
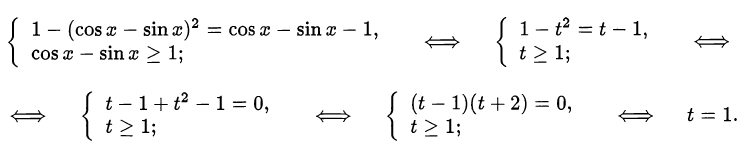
Возвращаемся к переменной 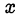 :
:
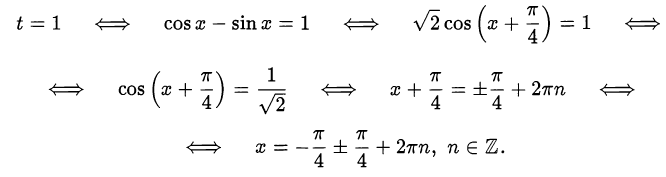
Ответ.
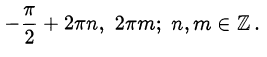
Пример оформления заказа №46.
Решить уравнение
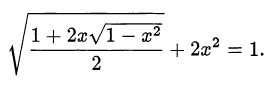
Решение:
Перепишем уравнение в виде

Из исходного уравнения получаем, что 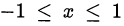 , поэтому можем сделать замену
, поэтому можем сделать замену 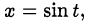 где
где 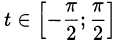 . Тогда с учётом ограничения на
. Тогда с учётом ограничения на 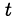 уравнение преобразуется к следующему виду:
уравнение преобразуется к следующему виду:

Вычислим 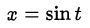 для найденных значений переменной
для найденных значений переменной 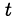 :
:
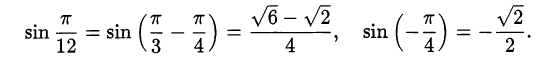
Ответ.