Оглавление:
Знакочередующиеся ряды. Признак Лейбница
Рассмотрим важный класс рядов, называемых знакочередующимися. Знакочередующимся рядом называется ряд вида
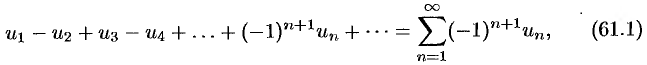
где 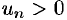 для всех
для всех 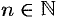 (т. е. ряд, положительные и отрицательные члены которого следуют друг за другом поочередно).
(т. е. ряд, положительные и отрицательные члены которого следуют друг за другом поочередно).
Для знакочередующихся рядов имеет место достаточный признак сходимости (установленный в 1714 г. Лейбницем в письме к И. Бернулли).
Теорема 61.1 (признак Лейбница). Знакочередующийся ряд (61.1) сходится, если:
- Последовательность абсолютных величин членов ряда монотонно убывает, т. е.
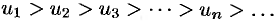 ;
; - Общий член ряда стремится к нулю:
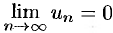 .
.
При этом сумма 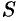 ряда (61.1) удовлетворяет неравенствам
ряда (61.1) удовлетворяет неравенствам

Рассмотрим сначала частичную сумму четного числа 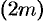 членов ряда (61.1). Имеем
членов ряда (61.1). Имеем
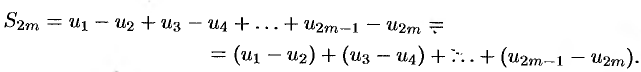
Выражение в каждой скобке, согласно первому условию теоремы, положительно. Следовательно, сумма 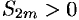 и возрастает с возрастанием номера
и возрастает с возрастанием номера 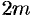 .
.
С другой стороны, 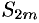 можно переписать так:
можно переписать так:
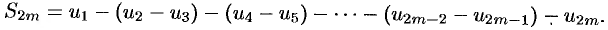
Легко видеть, что 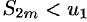 . Таким образом, последовательность
. Таким образом, последовательность 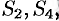
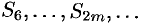 возрастает и ограничена сверху. Следовательно, она имеет предел
возрастает и ограничена сверху. Следовательно, она имеет предел 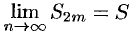 , причем
, причем 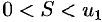 .
.
Рассмотрим теперь частичные суммы нечетного числа 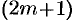 членов ряда (61.1). Очевидно, что
членов ряда (61.1). Очевидно, что 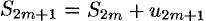 . Отсюда следует, что
. Отсюда следует, что
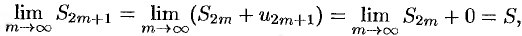
т. к. 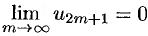 в силу второго условия теоремы. Итак,
в силу второго условия теоремы. Итак, 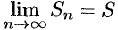 как при четном
как при четном  , так и при нечетном
, так и при нечетном  . Следовательно, ряд (61.1) сходится, причем
. Следовательно, ряд (61.1) сходится, причем 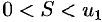 .
.
Замечания.
1. Исследование знакочередующегося ряда вида
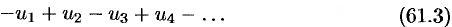
(с отрицательным первым членом) сводится путем умножения всех его членов на (—1) к исследованию ряда (61.1).
Ряды (61.1) и (61.3), для которых выполняются условия теоремы Лейбница, называются лейбницевскими (или рядами Лейбница).
2. Соотношение (61.2) позволяет получить простую и удобную оценку ошибки, которую мы допускаем, заменяя сумму 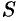 данного ряда его частичной суммой
данного ряда его частичной суммой 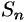 . Отброшенный ряд (остаток) представляет собой также знакочередующийся ряд
. Отброшенный ряд (остаток) представляет собой также знакочередующийся ряд 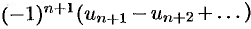 , сумма которого по модулю меньше первого члена этого ряда, т. е.
, сумма которого по модулю меньше первого члена этого ряда, т. е. 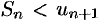 . Поэтому ошибка меньше модуля первого из отброшенных членов.
. Поэтому ошибка меньше модуля первого из отброшенных членов.
Пример №61.1.
Вычислить приблизительно сумму ряда
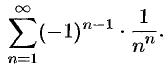
Решение:
Данный ряд лейбницевского типа. Он сходится. Можно записать: 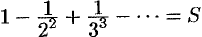 . Взяв пять членов, т. е. заменив
. Взяв пять членов, т. е. заменив 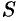 на
на
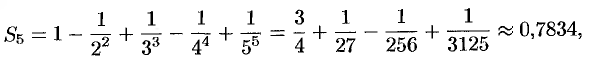
сделаем ошибку, меньшую, чем 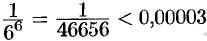 . Итак,
. Итак, 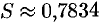 .
.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Радикальный признак Коши |
| Интегральный признак Коши |
| Общий достаточный признак сходимости знакопеременных рядов |
| Сходимость степенных рядов |
