Оглавление:
Знакопеременные и знакочередующиеся ряды. Признак Лейбница
Ряд, содержащий как положительные, так и отрицательные члены, называется знакопеременным.
Знакопеременный ряд 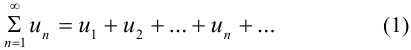
сходится, если сходится ряд, составленный из модулей его членов, т. е. ряд
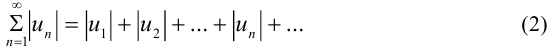
В этом случае ряд (1) называется абсолютно сходящимся.
Если ряд (2) расходится, то ряд (1) называется условно или неабсолютно сходящимся.
Теорема. Если ряд абсолютно сходится, то он сходится.
Ряд, у которого любые два соседних члена имеют разные знаки, т. е. ряд
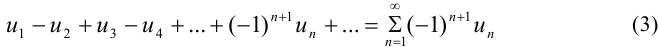
называется знакочередующимся.
Теорема (признак Лейбница). Если члены знакочередующегося ряда удовлетворяют условиям 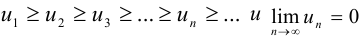 , то ряд сходится, и его сумма не превосходит первого члена.
, то ряд сходится, и его сумма не превосходит первого члена.
Доказательство. Возьмем последовательность 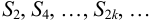 частичных сумм четного числа членов ряда. Имеем:
частичных сумм четного числа членов ряда. Имеем:
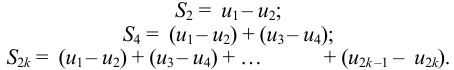
С другой стороны:
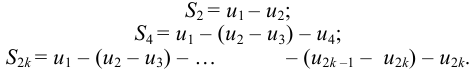
Из первого представления следует, что последовательность монотонно возрастает, являясь последовательностью положительных чисел. Из второго представления следует, что частичные суммы не превосходят  . Поэтому
. Поэтому 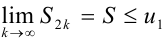 .
.
Покажем, что последовательность частичных сумм 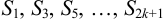 имеет тот же предел. Имеем
имеет тот же предел. Имеем 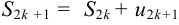 . Перейдя в равенстве к пределу, получим:
. Перейдя в равенстве к пределу, получим:
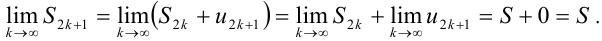
Теорема доказана.
Ряд, удовлетворяющий указанным условиям, называется рядом Лейбница.
Остаток 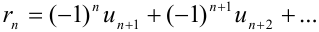 ряда Лейбница имеет знак своего первого члена и удовлетворяет условию
ряда Лейбница имеет знак своего первого члена и удовлетворяет условию 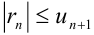 . Это неравенство удобно использовать для оценки погрешности, получаемой при замене суммы
. Это неравенство удобно использовать для оценки погрешности, получаемой при замене суммы  ряда её приближенным значением
ряда её приближенным значением
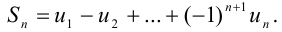
Задача №112.
Исследовать на сходимость и абсолютную сходимость ряд 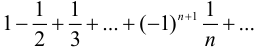
Решение:
Это знакочередующийся ряд. Он сходится по теореме Лейбница, так как 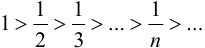 и
и 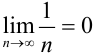 .
.
Ряд, составленный из модулей 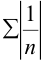 , расходится (гармонический
, расходится (гармонический
ряд). Значит данный ряд сходится условно.
Задача №113.
Сколько членов ряда
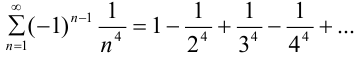 надо взять, чтобы вычислить его сумму с точностью до 0,0001?
надо взять, чтобы вычислить его сумму с точностью до 0,0001?
Решение:
Этот ряд знакочередующийся и удовлетворяет условиям признака Лейбница:
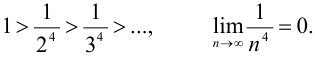
Следовательно, данный ряд сходится, причём абсолютно, так как
ряд 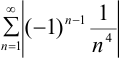 — сходится.
— сходится.
Определим число членов ряда, которые необходимо взять, чтобы вычислить его сумму с точностью до 0,0001.
Если 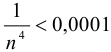 или
или 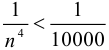 , то
, то 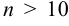 . Следовательно, нужно взять 10 членов данного ряда. Так как
. Следовательно, нужно взять 10 членов данного ряда. Так как 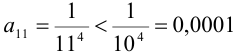 , то получаем следующую оценку для остатка ряда:
, то получаем следующую оценку для остатка ряда: 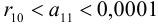 .
.
Этот материал взят со страницы кратких лекций с решением задач по высшей математике:
Решение задач по высшей математике
Возможно эти страницы вам будут полезны:
| Признак Коши задача с решением |
| Интегральный признак задача с решением |
| Степенные ряды задачи с решением |
| Ряды Тейлора и Маклорена задача с решением |
