Теорема об изменении момента количества движения

Теорема об изменении момента количества движения

Момент количества движения

Так как количество движения — вектор, имеющий определенную линию действия (и даже определенную точку приложения), то можно находить момент этого вектора относительно точки и оси так же, как определяли соответствующие моменты силы.

Сначала о моменте количества движения материальной точки.

Ее момент количества движения 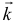относительно точки 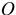по величине равен 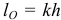, где 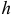— плечо вектора 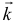с соответствующим знаком (+) или (-). Как вектор он определяется векторным произведением (рис. 19.6)

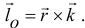
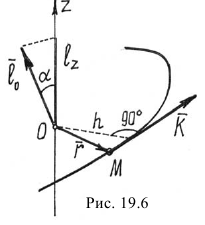
Момент количества движения 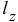относительно оси находится так же как находили ранее момент силы. И зависимость между моментами относительно точки и оси аналогична

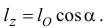
То есть момент количества движения материальной точки относительно оси равен проекции вектора момента количества движения относительно какой-либо точки 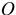, расположенной на оси, на эту ось.

Для движущейся материальной системы вводится понятие главного момента количеств движения относительно центра 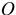как векторной суммы моментов количеств движения всех точек системы относительно этого центра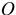

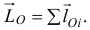
Вводится и понятие главного момента количеств движения относительно оси как алгебраической суммы моментов количеств движения точек системы относительно этой оси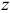

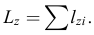
Зависимость между ними аналогична зависимости между соответствующими главными моментами сил

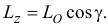
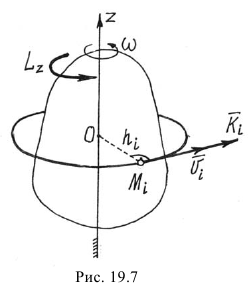
Главный момент количеств движения относительно оси равен проекции вектора главного момента относительно точки, расположенной на оси, на эту ось. Для твердого тела как материальной системы при некоторых движениях главный момент относительно оси определяется довольно просто.

Так, если тело вращается вокруг неподвижной оси 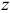(рис. 19.7), главный момент количеств движения относительно оси вращения

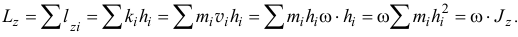
To есть равен произведению момента инерции тела относительно оси вращения на угловую скорость

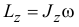
и направлен он по направлению вращения тела.

Если однородное тело имеет плоскость симметрии, перпендикулярную оси вращения, то вектор количества движения тела 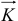расположен в этой плоскости на расстоянии 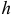от оси, равном

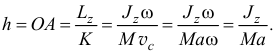
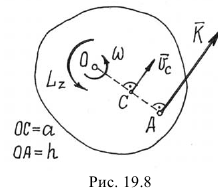
На рис. 19.8 показано сечение тела этой плоскостью симметрии и положение вектора количества движения 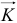. Заметим, что этот вектор приложен к той же точке 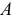, к которой приложена равнодействующая сил инерции точек тела 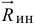(см. рис. 16.1).

Можно найти главный момент количеств движения тела и при плоскопараллельном движении относительно центральной оси 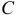(рис. 19.9). Скорость произвольно выбранной точки 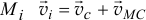, а соответствующие скоростям модули векторов количества движения равны 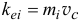и

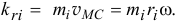
Главный момент количеств движения точек тела относительно оси 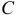, перпендикулярной плоскости движения:

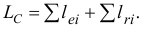
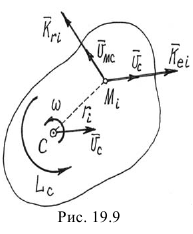
Но первая сумма равна нулю, так как по теореме Вариньона эта сумма моментов векторов 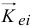равна моменту их «равнодействующей», которая приложена к центру масс 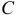, потому что переносное движение при плоскопаралельном движении поступательное (XIX, §2). Поэтому главный момент количеств движения будет равен

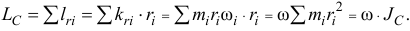
Значит, главный момент количеств движения точек тела при плоскопараллельном движении относительно центральной оси 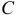, перпендикулярной плоскости движения, равен произведению момента инерции тела относительно этой оси на угловую скорость

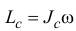
и имеет направление, совпадающее с направлением вращения, с направлением угловой скорости.

Аналогичный результат получается и для главного момента количеств движения относительно оси 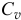, проходящей через мгновенный центр скоростей. Действительно, скорость точек тела 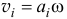(рис. 19.10) и главный момент

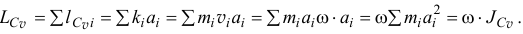
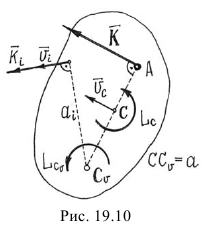
Итак

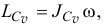
где 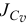— момент инерции тела относительно оси 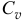, проходящей через мгновенный центр скоростей перпендикулярно плоскости движения.

При плоскопараллельном движении также можно найти положение вектора количества движения 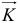(см. рис. 19.10). Он будет направлен параллельно скорости центра масс 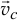и находиться на расстояниях от центра масс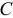

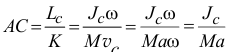
и от мгновенного центра скоростей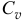

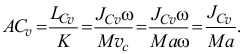
Очень похоже на результат, полученный при вращении тела вокруг неподвижной оси. Но разница в том, что здесь положение точки 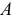меняется, так как меняется положение мгновенного центра скоростей .

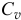Теорема о моменте количества движения

Рассмотрим движение материальной системы под действием внешних 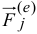и внутренних 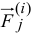сил .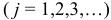

Определим момент количеств движения каждой точки этой системы относительно некоторого неподвижного центра 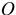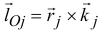и найдем его производную по времени

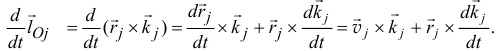
Первый член равен нулю, так как векторы 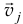и 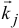совпадают по направлению. Так как по (19.7)

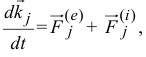
то второй член

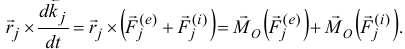
Поэтому

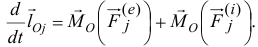
Сложим правые и левые части этих равенств, составленных для всех точек системы:

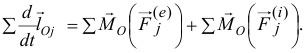
Вторая сумма в правой части равна нулю, так как главный момент внутренних сил относительно любой точки равен нулю. Оставшуюся часть равенства перепишем так:

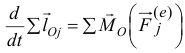
или

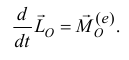
Производная но времени главного момента количеств движения материальной системы относительно неподвижной точки 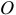равна главному моменту внешних сил, приложенных к системе, относительно той же точки .

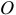Оказывается, точно так же формулируется эта теорема и относительно центра масс произвольно движущейся материальной системы. Действительно, рассмотрим движение системы как сумму двух движений: переносного — поступательного движения системы осей вместе с центром масс и относительного — относительно этих осей.

В разд. XIII, §3 мы установили, что движение точек, а значит, и всей материальной системы относительно движущейся системы координатных осей можно определять так же, как относительно неподвижных, если учесть переносные и кориолисовы силы инерции.

Значит, таким способом можно записать и теорему о моменте количества движения относительно движущегося центра масс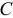

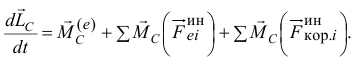
Но сумма моментов кориолисовых сил инерции равна нулю, так как при переносном поступательном движении эти силы отсутствуют. И первая сумма, сумма моментов переносных сил инерции, тоже равна нулю. Потому что по теореме Вариньона она равна моменту равнодействующей 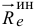этих сил, которая при переносном поступательном движении приложена к центру масс (см. XVI, §1).

Поэтому теорема об изменении количества движения относительно центра масс 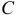движущейся системы записывается так же, как относительно неподвижной точки

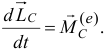
Спроектировав векторные уравнения (19.17) и (19.18) на какую-нибудь ось, проходящую через точку 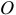или точку 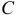, получим уравнения, с помощью которых и решаются задачи динамики:

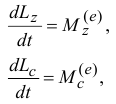
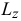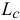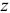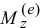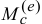где и — главные моменты количеств движения системы относительно неподвижной оси и оси , смотри выражение (19.13), а и — главные моменты внешних сил относительно этих осей.

К теореме о моменте количества движения следует сделать очень важные и полезные замечания. Если внешние силы на систему не действуют или действуют, но сумма моментов их относительно неподвижной точки 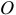или центра масс равна нулю, то по (19.17) и (19.18) 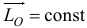и 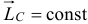. То есть главные моменты количеств движения относительно этих точек все время остаются постоянными.

То же самое можно сказать и о моментах относительно осей: если главный момент внешних сил относительно какой-нибудь оси 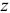, проходящей через неподвижную точку 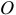, или относительно какой-нибудь оси , проходящей через центр масс системы, равен нулю, то главные моменты количеств движения системы относительно этих осей остаются все время постоянным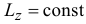и, и .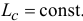

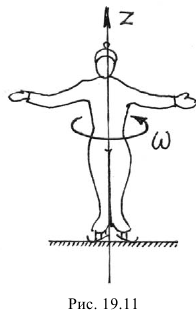
Например, на фигуриста, вращающегося на льду (рис. 19.11) вокруг оси 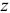, действуют внешние силы — вес и реакция гладкого льда.

Моменты их относительно оси 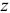равны нулю. Поэтому 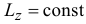. Но 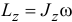, значит, 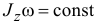. Отсюда следует, что если уменьшится момент инерции 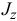(фигурист прижмет руки к туловищу), увеличится скорость вращения.

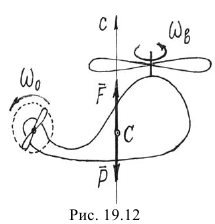
Еще пример. Вертолет, неподвижно висящий в воздухе (рис. 19.12). Лопасти винта вращаются с угловой скоростью 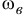. Вес вертолета 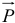уравновешивается подъемной силой 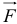. Момент их относительно вертикальной оси равен нулю. Поэтому .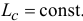

Если изменится скорость вращения винта 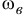, изменится и момент количества движения винта 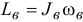.A чтобы общий момент количеств движения вертолета остался прежним, необходимо вращать корпус вертолета с угловой скоростью 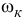. так, чтобы обязательно выполнилось условие

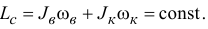
Значит, если винт увеличит угловую скорость, корпус начнет вращаться, но в противоположном направлении; уменьшит — корпус начнет вращаться в том же направлении. Чтобы не произошло этого нежелательного явления, у некоторых типов вертолетов предусмотрен еще один винт на хвосте, вращающийся в вертикальной плоскости и создающий горизонтальную внешнюю силу. Эта сила и будет ликвидировать вращение корпуса изменением момента .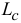

Несколько примеров на решение задач с помощью этой теоремы.

Эта теория взята со страницы помощи с решением заданий по теоретической механики, там найдёте другие лекции и примеры решения задач или сможете заказать онлайн помощь:

Помощь по теоретической механике

Кстати возможно вам будут полезны эти страницы:

Теорема о движении центра масс

Теорема об изменении количества движения

Дифференциальные уравнения вращения твердого тела

Дифференциальное уравнение вращения тела при плоскопараллельном движении