Оглавление:


























Б. Критическое состояния
- Дифференциальные условия устойчивости, которыми мы пользовались в гл. 3, § 6, и гл. 6, § 8, получены в предположении, что свободная энергия представляет собой аналитическую функцию надлежащим образом выбранных параметров состояния. Для гетерогенных систем это не всегда так. Рассмотрим прежде всего равновесие двухфазной системы, которая представляет собой смесь газообразной и жидкой фаз некоторого чистого вещества. На фиг. 22 показана типичная PVT-поверхность для такой системы. Линии Т = const на этой поверхности, т. е. изотермы в обычной проекции на PV-плоскость, нам уже знакомы (см., например, фиг. 2). На этот раз мы проведем также линии V== const (т. е. изохоры в проекции на РГ-плоскость) и линии Р = const, т. е. изобары в проекции на TV-плоскость (фиг. 23 и 24).
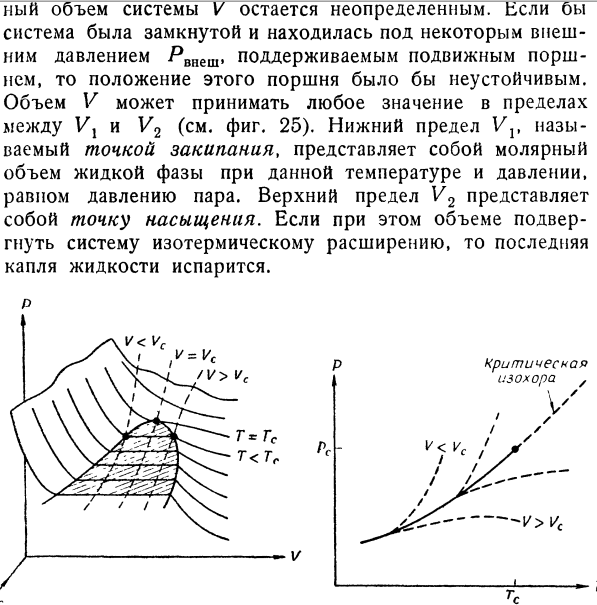
Кривая равновесия фаз показана сплошной кривой. На фиг. 23 ее проекция представляет собой кривую давления пара, которая, таким образом, показана дважды. На фиг. 24 кривая равновесия фаз представляет собой кривую ортобарических объемов: левая ветвь VX(JT) представляет собой молярный объем жидкости, а правая ветвь V2(T)— молярный объем насыщенного пара при заданной температуре (давлении). Чтобы рассмотреть устойчивость состояний системы, нам потребуется также график свободной энергии F (V) при постоянной температуре. Общий характер этой кривой, изображенной на фиг. 25, можно установить, исходя вой, изображенной на фиг. 25, можно установить, исходя из соотношений p — (L\ (L\ — d2F \dV)T’ \dV)T~ dV* ’ Если при некоторой заданной температуре обе фазы находятся в равновесии, то давление определяется точкой Р = Р(Т) на кривой давления пара (см. фиг. 23), но пол- ный объем системы V остается неопределенным.-Если бы система была замкнутой и находилась под некоторым внешним давлением Ртет, поддерживаемым подвижным поршнем, то положение этого поршня было бы неустойчивым.
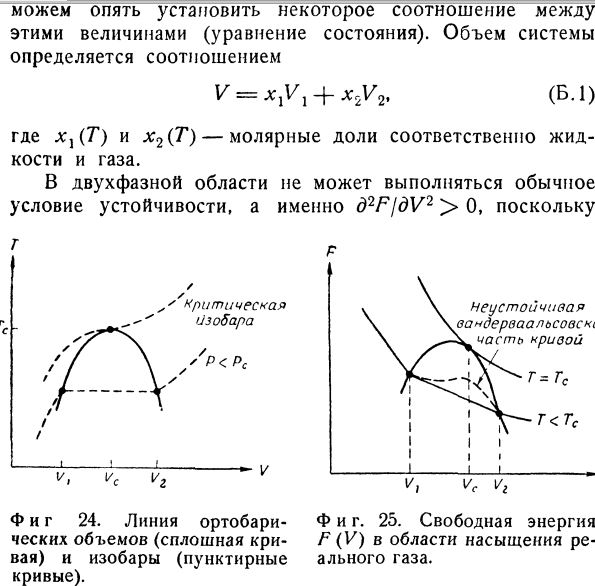
Объем V может принимать любое значение в пределах между Vj и V2 (см. фиг. 25). Нижний предел Vv называемый точкой закипания, представляет собой молярный объем жидкой фазы при данной температуре и давлении, равном давлению пара. Верхний предел V2 представляет собой точку насыщения. Если при этом объеме подвергнуть систему изотермическому расширению, то последняя капля жидкости испарится. р Фиг. 22. Термодинамическая поверхность (PVT) в области насыщения реального газа. Ф и г. 23. Кривая давления пара (сплошная линия) и изохоры (пунктирные линии). В отличие от равновесия в гомогенных системах, объем которых однозначно определен при заданном количестве вещества уравнением состояния, в двухфазной области объем не является однозначным экстенсивным параметром. Следовательно, объем V является неопределенным, по крайней мере в интервале от Vх до V2. Конечно, мы можем изменять объем как экстенсивный параметр и задавать любое его значение; необходимо помнить только, что объем V не связан функционально с Р и Т. Правда, задавая относительные количества сосуществующих фаз, мы можем опять установить некоторое соотношение между этими величинами (уравнение состояния). Объем системы определяется соотношением (Б.1) V = xlVl + x2V2, где х}(Т) и х2(Т)— молярные доли соответственно жидкости и газа. В двухфазной области не может выполняться обычное условие устойчивости, а именно d2FjdV2 > 0, поскольку Неустойчивая вандерваальсовск1 часть кривой Фиг. 25.
Свободная энергия F (V) в области насыщения реального газа. ’ критическая изобара — V Фиг 24. Линия ортобари-ческих объемов (сплошная кривая) и изобары (пунктирные кривые). (см. фиг. 25) (dF/dV)T = — Р = const в пределах целого интервала значений. Однако за пределами этого интервала, т. е. при V < Vj или V > V2, мы имеем обычное условие устойчивости по отношению к малым изменениям объема: \d2FjdV2)T=—(dPidV)T > 0. Следовательно, условие устойчивости двухфазной области имеет иной вид, а именно (dF)T > 0 для конечных вариаций bV за пределами этой области. Очевидно, что ни одна аналитическая функция не может иметь следующие свойства (см. фиг. 25): dF — = const при l/j < V < 1/2, WT > 0 ПРИ V < Vx или V > V2. Стандартный метод феноменологической термодинамики заключается в том, что вместо одной неаналитической функции ^(V) для описания указанного случая вводят две аналитические функции, а именно функции /71=Л//1(7\ vx) для жидкой фазы /72 = Л//2(Г, v2) для газообразной фазы. При заданной температуре Т <^ТС обе фазы могут существовать одновременно, если значения их плотностей соответствуют ортобарическим объемам Vx = Nvx(T) и V2 — Nv2(T).
В этом выражении хх и х2=\—хх представляют собой линейные функции V, определяемые уравнением (Б. 1), a Fv F2 не зависят от объема в рассматриваемой двухфазной области. Следовательно, используя (Б.1) и (Б.2), мы получаем Шг = Mw I+= » = «»’• Кривой, показанной на фиг. 25, соответствует функция, все производные высших порядков d»FjdVn от которой обращаются в нуль. Из уравнения (Б. З) получаем соотношение ^насыш.== ду» » (^.4) которое связывает давление насыщения с изменением свободной энергии при фазовом переходе. Это, конечно, просто иной способ записи обычного условия равновесия между двумя фазами: 0 = AF—PAV = AG = N Aji или [А, = Это условие можно записать также в виде \ а’ /на сыт эквивалентном уравнению Клапейрона. Из уравнения (Б. З) получаем соотношение ^насыш.== ду» » (^.4) которое связывает давление насыщения с изменением свободной энергии при фазовом переходе. Это, конечно, просто иной способ записи обычного условия равновесия между двумя фазами: 0 = AF—PAV = AG = N Aji или [А, = Это условие можно записать также в виде \ а’ /на сыт эИз уравнения (Б. З) получаем соотношение ^насыш.== ду» » (^.4) которое связывает давление насыщения с изменением свободной энергии при фазовом переходе.
Свободная энергия полной системы имеет в этом случае вид взвешенной суммы F = xxF, + x2F2. (Б.2) Людмила Фирмаль
- Это, конечно, просто иной способ записи обычного условия равновесия между двумя фазами: 0 = AF—PAV = AG = N Aji или [А, = Это условие можно записать также в виде \ а’ /на сыт эквивалентном уравнению Клапейрона. квивалентном уравнению Клапейрона. В теории ван дер Ваальса к выводу этих результатов подходят по-иному. Вместо того чтобы составлять функцию свободной энергии из двух различных ветвей Fj и F2, рассматривается лишь одна функция F, которая должна охватывать весь интервал. В этой теории определение давления насыщения и ортобарических объемов по правилу Максвелла означает построение общей касательной, проходящей через две точки Vx и V2f F{ (Б.6) _ dF v~ W dF dV V%-Vx v к кривой, которая соответствует одной аналитической функции F. По мере повышения температуры область существования двух фаз сокращается.
Прямолинейный участок кривой F становится все короче и короче, пока, наконец, ортобарические объемы Vx и V2 не сольются: в критической точке плотности обеих фаз принимают одинаковые значения. Ван дер Ваальс определил эти точки двумя уравнениями: (#)г = 0 и (£)_.. (Б.7, хотя впервые на существование этих критических точек указал Эндрюс (1863). Поскольку dP/dV = d2F/dV2t критическая точка характеризуется, очевидно, некоторым отступлением от обычного условия устойчивости. Чтобы состояние, в котором вторая производная d2FjdV2 обращается в нуль, было устойчивым, третья производная должна, разумеется, также равняться нулю [иначе величина 6F при некоторых вариациях была бы отрицательной].
Наиболее сильное условие устойчивости, которое можно представить себе в этом случае, имеет вид dF > 0. (Б.8) dV4 Это условие принято и в теории ван дер Ваальса. Здесь читатель может спросить, нельзя ли вместо (Б./ и (Б.8) рассмотреть еще более слаб)ю форму услови устойчивости, например dnF о при п — 2, 3, 4, 5, (Б.9) ^>0. (Б. 10) Оказывается, если F является аналитической # функцией объемов на критической изотерме, то это невозможно. В однокомпонентной системе имеется всего три параметра состояния Р% V, 7\ и, вообще говоря, мы не можем наложить более двух дополнительных условий (Б.7), помимо уравнения состояния. Если в качестве уравнения состояния взято уравнение ван дер Ваальса, свободная энергия имеет производные dnFjdVn всех порядков всюду и критическая точка однозначно определяется двумя уравнениями (Б.7). Условие, заключающееся в том, что функция F(TC, V) должна быть аналитической, можно, по-видимому, рассматривать как математически простую, но очень сильную формулировку принципа непрерывности перехода из жидкого в газообразное состояние, принадлежащего Энд-рюсу и ван дер Ваальсу.
Требования к степени непрерывности перехода, вытекающие из экспериментальных данных, могут быть, вероятно, слабее, чем требование, рассмотренное выше, однако мы будем придерживаться классической теории, в которой условия (Б.7) и (Б.8) означают дифференциальную устойчивость и максимальную непрерывность перехода между жидкой и газообразной фазами. На традиционном изображении термодинамической попервости (см. фиг. 22) геометрическое место фазовых переходов представляет собой острую кромку или узкий желобок (кроме ближайшей окрестности критической точки).
- Поэтому производные величины, например удельная теплоемкость, должны быть разрывны, по крайней мере при переходе через эту линию. Некоторые такие сингулярности имеют простой качественный смысл, который можно уяснить, не прибегая к точному уравнению состояния. Например, очевидно, что удельная теплоемкость при постоянном давлении в пределах двухфазной области должна быть бесконечно велика: если количество тепла, сообщаемого системе в таком состоянии, и давление поддерживаются постоянными, то прежде чем температура сможет повыситься, должно испариться конечное количество жидкости, а поскольку теплота парообразования конечна, это означает, что теплоемкость Ср бесконечно велика1). Удельная теплоемкость при постоянном объеме Си, напротив, конечна в области сосуществования фаз. Поэтому поведение этой величины, в особенности вблизи критической точки, представляет значфсительно больший интерес и приводит к важным следствиям в теории уравнения состояния. Зависимость Cv от объема описывается общим уравнением (см. задачу в гл. 2, § 7, п. 1)
Эту зависимость можно, таким образом, вычислить, измеряя кривизну изохор. Разработка этого весьма сложного метода, начатая Юнгом в 1895 г., недавно была завершена Микель-сом с сотрудниками. Как показано на фиг. 23, кривизна (д2Р/дТ2)у положительна при V < Vс и отрицательна при V > Vс. Поэтому удельная теплоемкость Cv должна иметь максимум на критической изохоре, что подтверждено прямыми калориметрическими измерениями. Один из явных недостатков уравнения ван дер Ваальса состоит в том, что оно предполагает условие (д2Р/дТ2)у = 0 в области существования одной фазы и, таким образом, не в состоянии объяснить появления указанного максимума удельной теплоемкости. Рассмотрим теперь область существования двух фаз. Внутреннюю энергию и удельную теплоемкость двухфазной системы можно выразить следующим образом: U = xlUl -f- x2U2> (Б Л 2) су-(#)»+•- <«.- «■> (4Н, ■ <в.1 з>
Необходимо четко различать производные (dUJdT)v и (dU2/dT)v, стоящие в правой части уравнения (Б. 13), и 1) В критической точке теплота парообразования равна нулю, но в этой точке теплоемкость Ср бесконечно велика по другой причине. молярные теплоемкости CIV и C2V жидкости и газа при постоянном объеме. Величины U] и U2 следует рассматривать как функции их(У,, Т) и U2{Vv Г), где ортобари-ческие объемы Vx и 1/2 зависят только от Т. Таким образом, мы должны подставить в (Б. 13) следующее выражение: (дил / дил. / Я/, \ / </1Л \ =cv+[T$r)v-p +( С7- V \ йТ )Vt \dVjT\ dT ;сосущ dVy dT (Б. 14) сосущ и такое же выражение для dU2jdT. В последнем члене уравнения (Б. 13) можно заменить разность U2 — U, в соответствии с (Б.5): и, = [(г -^г—р) (У 2 — ^)]сосуш • (В. 15) Эта разность обращается в критической точке в нуль, но в уравнении (Б. 13) она умножена на величину (dx2fdT)Vt которая в критической точке бесконечно велика: I дх2 \ = [х, (dVJdT) + х2 (dV2/dT))cocyul \ (УГ )v Vl — V2 ′ Подставляя уравнения (Б. 14) — (Б. 16) в уравнение (Б. 13), получаем
4- дг2 {соответствующее выражение для фазы 2}. (Б. 17) Это выражение можно несколько упростить, исключив производную = Ы^сосущ _ (ж)г («всосут’ (Б1 8) Удельную теплоемкость для двухфазной системы можно окончательно записать в виде Рассмотрим теперь величину Cv> следуя Уленбеку и Хем-меру [31]. Если мы приближаемся к критической точке из двухфазной области вдоль критической изохоры V — Vc, то распределение между фазами приближается к 1: 1 или х1—>х2—>Ч2 и удельные теплоемкости Cw и C2V сосуществующих фаз приближаются к одному и тому же значению, а именно к удельной теплоемкости вещества в прилегающей однофазной области.
Изменение величины Cv при пересечении линий перехода Cv{Tc-0)-Cv(Tc + 0) равно, таким образом, пределу ri’r-0 ~ Т [(ж»)г ( )сосущ + Ыт)г ( ИГ )сосуШ] ’ (Б.20) Эта формула должна быть общей; она не содержит никаких дополнительных специальных предположений относительно критического состояния, кроме условия Vx—V2—Vc. Однако, чтобы вычислить предельные значения производных, входящих в (Б.20), необходимо сделать более определенные предположения. Уленбек и Хеммер использовали уравнение состояния ван дер Ваальса в универсальной форме (я + ^г)(Зсо-1) = 8в, где давление, объем и температура описываются приведенными параметрами n — PjPr co = V/Vrcf 9 — TjTc. Поскольку нас интересует только окрестность критической точки, разложим л в ряд по степеням малых величии т = 1 — 0 и е = (О — 1 и получим л = 1 — 4т+6те — 9те2~~е3+__ (Б.22) Мы можем теперь найти ортобарические объемы, используя правило Максвелла, записанное в виде (Oj J со г/л-— 0, л((о1) = л(<о2), (Б.23) со, (Б.21) где со, = 1 —и со2 = 1 -|-в2. При учете членов третьего порядка включительно это дает два уравнения для определения и е2: 4т (ej -И2)+ 4т (ef — С2) — е] — eij = О, 4т (е, + е2) — 6т (— е) — е? — е* = 0. (Б’24)
В этом приближении, достаточном для наших целей, находим е1 = е2 = 2т’/з; (Б.25) иными словами, линия перехода вблизи критической точки должна иметь вид параболы: (со — 1)2 = 4т. (Б.26) Для вычислений выражения (Б.20) нам потребуются следующие производные: \ d0 /сосущ =6т— 18те — = \ /0 2 1 = — 12т ± член порядка т/, в (Б’27> где верхний знак относится к жидкой, а нижний знак — к газообразной фазам. Поскольку (dco/dQ)2 и дл[д<о стремятся соответственно к бесконечности и к нулю таким образом, что их произведение стремится к конечной величине, равной —12, из выражения (Б.20) видно, что Су, согласно этой теории, претерпевает в критической точке скачок на конечную величину. Подставляя вандервааль-совское значение критического отношения (см. гл. 1, § 2, п. З), PcVc! RTc = 3lz, получаем для скачкообразного изменения.
Уравнение ван дер Ваальса нельзя считать пригодным для количественных предсказаний. Людмила Фирмаль
Существенный вопрос заключается в том. правильны ли качественные результаты, а именно конечный скачок величины Су и параболическая вершина линий перехода в критической точке, поскольку эти выводы можно рассматривать как следствия принятых предположений относительно критической точки, являющихся, вероятно, более общими, чем любое конкретное уравнение состояния. Ни одно из них, однако, по-видимому, не подтверждено экспериментами. В частности, как сейчас полагают, удельная теплоемкость Су имеет в критической точке логарифмическую особенность (работа Воронеля с сотрудниками, 1964)1). Среднеарифметическое ортобарических плотностей следует с известной степенью точности правилу прямолинейных диаметров, сформулированному Кайете и Матиасом (1886).
Используя приведенные величины, это правило можно записать в виде где р — постоянная порядка единицы. с)то эмпирическое правило может быть с успехом применено для экстраполяции измерений к критической точке. Линейную экстра-поляционную формулу этого вида можно вывести из уравнения ван дер Ваальса, продолжив разложение (Б.22) до членов пятого порядка. Получаемая таким образом безразмерная постоянная р имеет приемлемое значение, хотя опять-таки не следует рассчитывать на получение точных количественных результатов. До сих пор мы говорили только о равновесии между газообразной и жидкой фазами чистого вещества. Общее представление о критической точке связано с явлением, состоящим в том, что гетерогенную систему можно в некоторых случаях привести в состояние, в котором исчезновение различия между обеими фазами происходит непрерывно.
Гиббс определил критическое состояние как состояние, в котором исчезает различие между двумя сосуществующими фазами. Это относится и к случаю равновесия газ — жидкость, который мы уже рассмотрели. Далее, две одновременно существующие жидкие фазы также могут находиться в критических состояниях. Если же одна из сосуществующих фаз или обе эти фазы твердые, то, по-видимому, ни о каком критическом состоянии в указанном выше смысле говорить нельзя. Твердая фаза не может быть полностью описана с помощью только непрерывно изменяющихся параметров. Твердая фаза характеризуется некоторой определенной кристаллической структурой, а такая характеристика не может исчезать непрерывно. Тем не менее, по-видимому, возможно, что ортобарические объемы двух сосуществующих твердых фаз могли бы приближаться друг к другу и, в конечном счете, совпасть. Действительно, церий в твердом состоянии обладает двумя различными фазами, имеющими одинаковую кристаллическую структуру.
Имеются также убедительные доказательства наличия критической точки на кривой равновесия между этими фазами. Наиболее известные примеры критических явлений дают некоторые бинарные жидкие смеси, обладающие ограниченной смешиваемостью. Если две такие жидкости тщательно перемешаны в отношении х — NJ(Nl— N2)> которое находится за пределами области смешиваемости, то система в равновесном состоянии не будет однородной, а распадается на две фазы с различными концентрациями л;’ и л;». В этом случае, согласно правилу фаз Гиббса, термодинамические состояния системы обладают двумя степенями свободы. Термодинамические состояния можно изобразить поверхностью в системе координат х, 7\ Р. Проектируя сечения этой поверхности плоскостями P=const на плоскость Txt получаем семейство кривых f(xy Т) = 0.
Существует несколько характерных форм этих кривых, часть из которых имеет важное значение для технических приложений. Здесь нас будут интересовать только такие типы кривых, которые обнаруживают критические точки, поэтому кривая f(x, Т) должна быть по своей форме аналогична ортобарической кривой (см. фиг. 24). В тех случаях, когда могут одновременно существовать две фазы, уравнение f(x, Т) = О имеет при данной температуре два решения: х’(Т) и х»(Г). При изменении температуры длина кривой Т = const, соединяющей х’ и х» > может увеличиваться или уменьшаться. Если при некоторой температуре эта кривая обращается в точку х’ = х’\ то мы уже не можем различать две фазы, и состояние становится критическим. Такие критические точки для раствора могут лежать как выше, так и ниже области сосуществования двух фаз. В некоторых случаях кривые f (x, Т) могут даже быть замкнутыми. Если не считать этих ограничений, то критические точки для раствора, по-видимому, Совершенно аналогичны критической точке для равновесия между газообразной и жидкой фазами.
Для системы жидкость — жидкость значительно проще, конечно, рассматривать правило прямолинейного диаметра и форму вершины кривых перехода. На практике парабола, соответствующая уравнениям (Б.25) и (Б.26), недостаточно хорошо описывает форму вершины кривых’перехода. Много теоретического и экспериментального материала по данному вопросу содержится в книге Роулинсона [32], отражающей современные взгляды. В рассмотренном случае бинарных смесей критические точки можно в полной аналогии с вандерваальсовскими условиями (Б.7) и (Б.8) характеризовать соотношениями <■>*> поскольку в области сосуществования фаз переменная х является неопределенной. В остальном рассмотрение проводится так же, как и выше. В гомогенной смеси с с компонентами термодинамическое состояние имеет с— 1 степень свободы (см. гл. 6, § 6, п.1).
Если критическое состояние определено наложением двух дополнительных условий, соответствующих (Б.7) или (Б.9), то оно будет иметь соответственно с — 1 степень свободы. Обычное условие устойчивости гомогенной системы состоит в том, что некоторая квадратичная форма должна быть положительной. Для выполнения этого условия необходимо и достаточно, чтобы все собственные значения этой формы были положительными. В критической точке эта квадратичная форма вырождается, т. е. одно из собственных значений стремится к нулю (или к бесконечности) при асимптотическом приближении к некоторому состоянию. Если
форма, определяющая устойчивость, представляет собой сумму квадратов, то это условие совпадает с условиями (Б.7) или (Б.9). Если число компонентов больше двух, то возникает осложнение, связанное с тем, что в форме, определяющей устойчивость, могут появиться перекрестные члены d2F/dNidNk Ф 0 (см. гл. 6, § 8). В этом случае необходимо сначала привести форму к главным осям, Переменная, являющаяся неопределенной в двух- фазной области, будет представлять собой некоторую фиксированную линейную комбинацию числа частиц.
Иначе ситуация была бы такой же, как и в случае двух компонентов, когда в критической точке одно собственное значение обращается в нуль. Это приводит в точности к двум условиям типа (В. 7). Приведенное выше описание критических состояний впервые было дано Гиббсом. Поскольку нельзя быть уверенным в справедливости этого описания, мы не будем рассматривать его более подробно.
Смотрите также:
| Примеры | Множители Лагранжа |
| А. Некоторые физические константы | Преобразования Лежандра |
