Оглавление:





Безвихревое осесимметрическое движение при. Метод Франкля
Безвихревое осесимметрическое движение при. Метод Франкля. Если вихря нет, то есть b = 0, то, в соответствии с характеристиками первого семейства, он выглядит та. В соответствии с характеристиками 2-го семейства. Задача расследования такого хода была впервые решена Франклом. Вместе с плоскостью (z, r) рассмотрим плоскость (vz,vr). Точно так же, как и в случае плоской задачи, точки плоскости между окружностями соответствуют движению.
Смотрите также:
Что такое уравнение Бернулли? Здесь она написана точно так же, как плоская задача. Однако, свойства плоскости (z, r) перестать быть эпициклоиды и, более того, не может быть найден, а также свойства плоскости (р, d) до тех пор, пока движения определяется. Это происходит из-за наличия правой стороны в (26.1) и (26.2).
Эта задача оказывается формально аналогичной случаю плоского вихревого движения. Дело в том, что зависимость вдоль характеристик плоскости вихревой задачи представлена в виде неинтегрируемых комбинаций. Людмила Фирмаль
- А в практических расчетах она была заменена уравнениями типа (13.4), (13.6) .Однако, (2 .1), (26.2) отличается от (9.18), (9.19) в том, что в дополнение к тому, что x и y вместо р и Р, только в виде коэффициентов х, (26.1) и (26.2) проще, чем коэффициенты в плоскости проблемы (последний содержится в количестве, которое определяется).
Что касается свойства плоскости (X, р), они определяются по формуле (25 .8) .Другими словами Свойства в плоскости (x, y) ; уравнение (25 .8) по-прежнему эквивалентно соотношению (n-норма характеристики); уравнение Бернулли верно в своей предыдущей форме. Вы можете легко нарисовать характеристику на плоскости (r,r).
Смотрите также:
Если обратиться к задачам типов 1, 2, 3 и 4, которые рассматриваются в § 11, то для приближенного (графического) решения здесь достаточно изучить следующие 3 операции: 1) найти скорость на пересечении характеристик разных семейств, возникающих из 2-х различных точек близости, где скорость уже известна; 2) найти скорость на пересечении с заданным элементом характерной стенки, где скорость выходит из точки, близкой к известной стенке; 3) найти скорость на пересечении характеристики, выходящей из точки, близкой к некоторой свободной поверхности и с заданным элементом этой свободной поверхности.
Смотрите также:
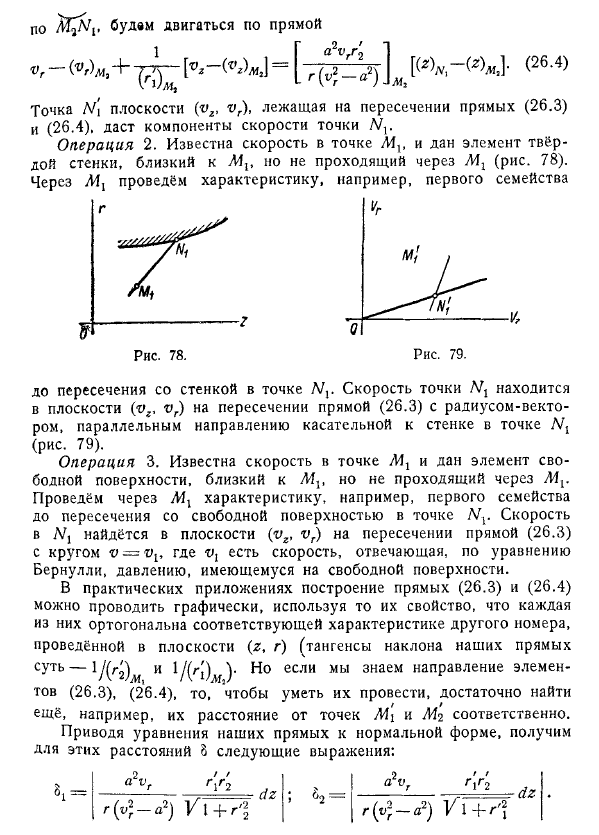
Сначала мы изучим операцию 1. Операция 1. Пусть точки близости самолета Mx и M2 сообщают вам скорость (рис . 77) .Отметьте точки в плоскости Vg) . Эта координата является составляющей скорости в точке. Через точки M1 и M2 нарисуйте элементы характеристик различных семейств, пока они не пересекутся с Ex . Эта конструкция может быть выполнена путем вычисления r (25.8).
Рассуждая так, чтобы найти скорость в какой-то момент. Перемещаясь вдоль элементов Mх в плоскости (z, r), перемещается вдоль элементов линии . Теперь, если вы установите символ Mx внутри скобки, выражение внутри скобки вычисляется в точке Mx. С другой стороны, движение Точка L в плоскости (x, y) на пересечении линий (26.3) и (2 .4) дает компонент скорости точки.
Кроме того, как и в плоской задаче, элементы характеристики необходимо заменить на те, которые касательны к характеристике. Людмила Фирмаль
- Операция 2 .Скорость точки известна и задается элементом сплошной стенки, который близок к Mx, но не проходит через Mg (рис .78) . Через Mx, например, выведите характеристики первой семьи Точка L7 на стыке со стеной. Скорость точки v находится в плоскости пересечения с линией (26.3) и радиус-вектором, параллельным направлению касательной к точке стенки (рис .79).
Операция 3 .Скорость в точке Mx известна, и ей задается элемент свободной поверхности, близкий к A1X, но не проходящий через M. Например, нарисуйте характеристики первого семейства до тех пор, пока они не пересекут свободную поверхность в точке. Скорость Ex будет плоскостью на пересечении линий (26 .3) и окружности, согласно уравнению Бернулли, давление на свободную поверхность.
В реальном приложении построение линий (26.3) и (26.4) может быть выполнено графически с использованием характеристики, что каждая из них ортогональна соответствующей характеристике другой, нарисованной на плоскости (z, r) в направлении элемента (26.4), чтобы иметь возможность рисовать, например, достаточно найти точки и расстояние от M2, соответственно.
