Оглавление:




















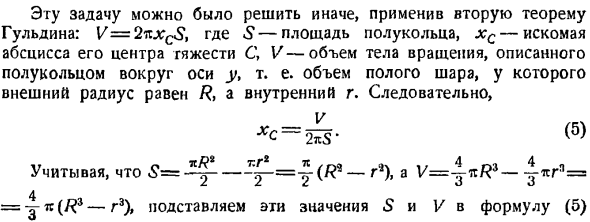







Центр тяжести
- Центр тяжести Дана результирующая система параллельных сил F] F Fiy Fn. Предположим, что точка приложения силы зафиксирована. Центр параллельной силы является точкой приложения равнодействующей силы, и если все параллельные силы вращаются на 1 угол при сохранении параллели, то равнодействующая сила имеет характеристику, что центр параллельной силы с поворачивается на один и тот же угол.
Координаты центров параллельных сил задаются формулой: С. С. С. 2 (это ФК * к)£(±Fkyk)£(Лt \ ЗК) с-^> уя -* ’ РС-м;-» £(±ФК) к — =) Грех. xc = r, yc = 0, где r-радиус окружности, а a-половина центрального угла. г)центр масс (рис. 2.18) области однородной веерообразной формы находится на оси симметрии, координаты xc = g、 = 0, где r-радиус окружности.
a-половина центрального угла. Людмила Фирмаль
д) центр масс C однородной призмы находится в середине сегмента, соединяющего CT и Cx центра масс между верхним и нижним основанием этой призмы(рис. 2.19). другими словами, CXC-CC f) центроид однородной пирамиды лежит на отрезке, соединяющем вершину o пирамиды и центроид Cx ее основания. Да. Центр тяжести основания пирамиды Ci (рис. 2.20) — OS=, т. е. CC, на расстоянии этого отрезка OS \、 г)центр тяжести однородного конуса находится на его высоте, с зазором 1/4 высоты от основания конуса (Рис. 2.21), то есть AC = ^ — OA. Успех выбора координатных осей играет важную роль в решении задачи определения местоположения центра тяжести однородного твердого тела.
Если твердое тело имеет плоскость симметрии, то 1 из осей координат (например, z>) должна быть ориентирована перпендикулярно этой плоскости. Поскольку центроид находится в плоскости симметрии, то есть плоскости xy, zc = 0, определяют только 2 координаты: xc и mustache. Если твердое тело имеет ось симметрии, необходимо объединить 1 из осей координат, например x, с осью симметрии. Поскольку центр масс находится на оси симметрии, или оси x, yc = zc = 0, определите только 1 координату xc. Формула (I*)、(2 *)、(3 )или (4) наиболее распространенным использованием является родственный психический срыв.
- Твердое тело, расположение центра тяжести каждой из таких частей известно или легко определить. Так, например, если разобрать площадь равномерного плана этажа, которая показана на рисунке 1, то положение центра тяжести 2,22, 3 части C (x0 усов, zc) определяется по формуле (3*). Л:, А,-Б-га Аса + ИФА АС3 yl * сл _ л. — F а,+ «АСЛ + АС2 + АС3′ с ~~’ Где xh y \ j Zj-координаты центра тяжести Cj в первой части вида в плане. — Площадь первой части и др. О Да. икс Рис. 2.23. Рисунок 2. 22. Икс
В некоторых случаях рекомендуется заменить твердое тело не общим, а с разницей отдельных parts. So например, для пластины с 2 вырезами показано на рисунке 2. 2. 23, его площадь может быть записана в виде разности между площадью сплошной плоской фигуры и площадью 2 вырезов 2 и 3.in в этом случае положение центра тяжести (xc, Kore, gc) однородного плана этажа определяется С〜а,-АС2-АС3’asl-как.- ’zc-у апу> Здесь. vj-координаты центра масс Ci твердой плоскости Площадь рисунка равна/; .Г2-координаты С * визитка 2 центр тяжести, его площадь равна Д% и так далее
Чтобы повысить точность результата, нужно разделить тело на большее количество частей, что усложняет решение задачи. Людмила Фирмаль
Выражение(1 *)、(2 *)、(3 )、при использовании или (4) метод разделения однородного твердого тела на отдельные части позволяет по координатам отдельного центра тяжести точно определить часть и ее площадь (объем или длину).так, для сплошной фигуры с криволинейным контуром или твердого тела с поверхностью сложной формы точность результата будет следующей: (
(5 *)、(6 *)、(7 ) или лучше использовать(8) Теорема Гульдина полезна, когда число данных и неизвестных включает: а) длина дуги вращения, расстояние от центра тяжести этой дуги до оси вращения, а также площадь поверхности вращения, представленная дугой (1-я теорема Гульдина). б) площадь повернутого вида в плане, расстояние от центра тяжести вида в плане до вращающегося вала и объем вращающегося тела、
Это описано в этом виде в плане (2-я теорема Гурдина). Задача 2.18.Определите расположение центра тяжести однородной ОАБД проволочной петли с, состоящей из 2 линейных отрезков ОА = Од = а и полукруглого Абд диаметром AD, расположенных под углом 60°(/_АОД = 60°) друг от друга(рисунок а). The solution. In в проволочной петле у нас есть ось симметрии, вдоль которой мы рисуем ось X. Получите начало координат в точке O и направьте ось y вверх по вертикали. Поскольку центроид c контура находится на оси симметрии X, _us = 0.To определите координату xc, используя формулу (4*). К задаче 2.18.
2 * к ХК * С = Л•(0 В этом случае рекомендуется разделить всю проволочную петлю на 3 части.2 отрезка прямой OA и OD длины a и радиуса a / 2, Добавить полукруг. Такая разбивка удобна тем, что нетрудно определить расположение центра тяжести каждой из этих частей. Сегмент OA представлен числом 1, сегмент OD-числом 2, а полукруг ABD-числом 3.После этого Формулу(1)можно записать следующим образом: д /,+ д/, + д /,»1」 Где, X1, X1-абсцисса отрезка OA и od центроидов C1 и C2 xz-абсцисса центроидов C3 полукруглого ABD, A /, M A / g-длина этих частей провода loop.
As вы можете видеть из диаграммы、 ОА НР, а / 3 / оч Х \ = ХВ =〜в COS 30°= -^ -. (3) для определения xb воспользуемся тем, что расстояние ECa от центра окружности дуги Ca до центра тяжести определяется по следующей формуле: В этом случае a = mc / 2, а следовательно r-a / 2, поэтому ZrC3 = a / ir. So … ар3 = 0£+ £ С3 = ол в COS 30°+—= «^ р-(4) Кроме того, существуют: Д / 1 = = Д Б = а, МС = Г (5) Подставляя (3), (4) и (5) в Формулу (2), получаем: a / 3 l, a / 3_, 2 + l / 3.
Таким образом, центроид петли провода OABD находится в точке C, где координаты hgs = 0.76 a, y = 0. Задача 2. 19.Определите расположение центра тяжести C от площади поперечного сечения однородного штампа, показанного на рисунке. один. Решение. Заметим, что в поперечном сечении имеется ось симметрии, проведем ось x вдоль оси симметрии, перпендикулярно ей, а сверху-ось Y.
Так как центроид к-образного сечения находится на оси симметрии, то есть на оси x, то необходимо только определить координату x0. Вычтите вспомогательные линии MP и NS и разделите поперечное сечение на сумму площадей 3 прямоугольников. Представляет прямоугольник MDBA с/, прямоугольник ENLK с номером 2 и прямоугольник NMPS с номером 3.Тогда Формула (3*) имеет вид «Asi в BSJ + ХВ как» М Поскольку центроиды прямоугольников Q, Ca и Ca находятся на пересечении диагоналей, это выглядит следующим образом: (2) xx = xy = 1 b см, xy = b см.
Площадь прямоугольника равна D51 = D ^ = 300 см \ D ^ s = 200 см \ Да.) [ Д.+ М 1о ч 1′ | Ви? П С Т Я ’\ / \ Л Что? £ — — — 30СМ — к (4) ХГ = Используя (2) и (3), запишем Формулу (1) в виде: 15-300-Ф-15-300 4-5. 200 10# = — зоопарк + Зоопарк + ^ о-т — * * с = 1 ^ см. Итак, центроид площади поперечного сечения штампа находится в точке С, где координаты jcc = 12,5 см, y = 0. Эту задачу можно решить несколько иным способом, проведя вспомогательную линию AL (рисунок B) и представив площадь этого участка.
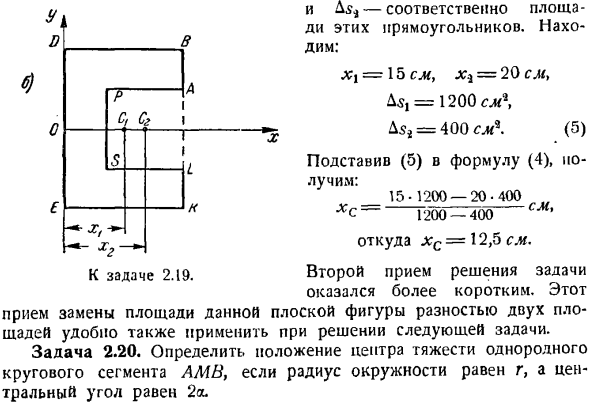
В виде разности площадей прямоугольника EBBK и SPAL запишем прямоугольник EBBK с номером/, прямоугольник SPAL с номером 2 и Формулу (3*) в виде. xi АСТ-х * АС2 ЗХ-а ’ Где DG] — абсцисса центроида Cj прямоугольного EDBK, jc4-абсцисса Ci продолговатого SPAL, Asj И s} — Это области этих прямоугольников, соответственно. Мы это выясним: x1 = \ b см, JCj = 20 см, As, = 1200 см \ D $ 2 = 400oL(5) В Г. Так… 7.- с ХГ. Да. Подставляя Формулу (4) в (5), получаем: 15-1200-20-400 Xc ~ ~ 1200 ~ 400 см%
Где XC = 12,5 см. 2-й способ решения проблемы был короче. Данная методика замены площади заданного плана этажа с разницей в 2 площади также удобно применяется при решении следующих задач: Задача 2. 20.Если радиус окружности равен r, а угол центра равен 2gl, определите положение центра тяжести однородного кругового сегмента AMB Л. И затем К заданию 2.19. Где xk> yk, zk-Координата точки действия силы Fk>.Где k = 1, 2,…и Н is. In эти формулы, Fk-величина force.
In в этом случае проекция силы считается положительной, если сила Fk и направление параллельной оси совпадают, и отрицательной, если направление силы Fk и параллельная ось противоположны. Если твердое тело расположено вблизи поверхности Земли, то к каждой из частиц вещества этого объекта прикладывается сила тяжести (предполагается, что материальные частицы распределены в твердом теле непрерывно).
Эти гравитационные силы образуют систему почти параллельных сил(они расположены на поверхности Земли, а гравитационная линия из 31 м2 частиц вещества образует угол, равный 1 секунде). Параллельный центр тяжести называется Plt P2, Pp Центр тяжести твердого тела C, а также сумма центра тяжести всех его материальных частиц, называется весом твердого тела P.
Координаты ХС, У0 zс центра тяжести С твердого тела, даются приближенные формулы. С. С. С. фут = л Решение. Выберите ось. Направьте ось x вдоль оси симметрии, возьмите начало координат к центру окружности O и направьте ось y вертикально вверх. Поскольку центр масс кругового отрезка AMB находится на его оси симметрии, то есть на оси x, yc = 0.Абсцисса центра тяжести С остается определить ХС. Сектор OAMW и площадь равнобедренного треугольника ОАВ как^, то есть 5 = А,-а、 Теперь выражение (3 *)можно записать в виде: _ Как — Гоа、 Как,—Как、• Где Xi и xy — координаты абсцисс центроидов Q и C * cr соответственно.
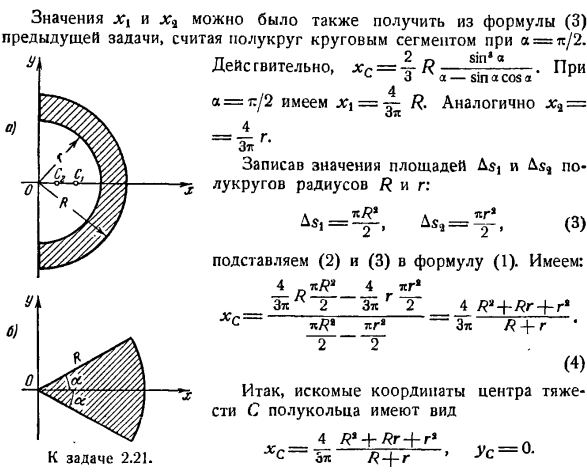
Таким образом, координаты центроида C кругового сегмента являются Нравится * sin8 а л 0 ХС-ПГ -:-США = 0-(3) L Za-sin A COS a ’ Задача 2. 21.Определите положение центра тяжести однородного полукруга, если внешний радиус и внутренний радиус равны R и g соответственно. Решение. Если вы укажете ось x вдоль оси симметрии полукольца(рисунок а), то y = 0
.Начало координат получается в центре полукольца O, а ось y направлена вертикально вверх. Чтобы определить абсциссу xc центроида C, представим площадь полукруга в виде разности между 2 областями полукругов радиуса R и R. 3) и можем записать О Где X \и X} — абсцисса Ci и C полукруга радиуса и r соответственно. в XT может быть определена как абсцисса центра тяжести круга. a = сектор mc / 2(Рисунок b).
смотрите обзор ХС = ^( ), То есть<* = — £ — xx = — R. аналогично= 4, 4 4 значения x {и lx также могут быть получены из предыдущего выражения задачи(3).Рассмотрим полукруг как круговой сегмент a =т / 2. значение x можно также получить из предыдущего уравнения (3), рассматривая полукруг как круговой отрезок a =т/ 2. Дэйс, ХС = — Р см * в. г -/\ -: -.Так… s 3 a-sin A COS A r 4 есть a =π/ 2, π,= — R. аналогично, xy = 4. Zgyo Г * ТС /? » (3)
Мы записали площадь полукруга радиуса R и значения АСТ и А. Л. Г1. Подставим уравнения (1) (2) и (3).У нас есть: компания LG. * ЗП 2 37t Д 2_ _ я ЗТС. лг1. Два (4) Таким образом, искомые координаты центра масс с-кольца имеют вид: 07С. Задача решается по 2-й теореме Гульдина, V = 2kXqS, где 6 * — площадь полукруга, xc-искомая абсцисса его центра тяжести C, а V-объем вращающегося тела, представленного полукругом вокруг оси y, то есть радиус внешней окружности полости равен шару. = 2С-(5) С = — Р*), А в = ^ РИ— «РЖ = 4. =И (Р?- r3), подставим эти значения 5 и V в формулу(5 И мы получаем; „3 *(/? ’- г“) 4 + +
Сравнивая оба способа решения задачи, один 1 должен отдать предпочтение 2-му способу. Решение было коротким, кроме того, не было необходимости использовать формулу для определения абсцисс xc. 4. Центр тяжести кругового сектора C xc = ^ R Однако следует отметить, что применение теоремы 2-го Гульдина является эффективным. Это связано с тем, что расчет площади плана пола полого шара (полукольца и объема вращающегося тела) не представляет сложности.
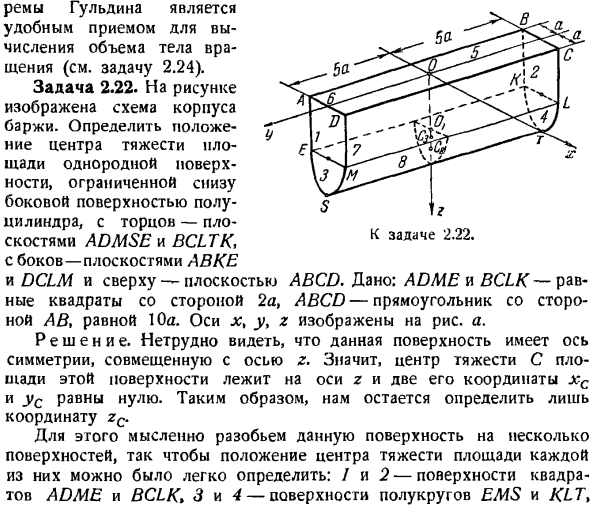
Если расчет объема вращающегося тела трудоемкий, то применение теоремы 2-го Грудина нецелесообразно. При этом в зависимости от состояния задачи известны площадь плана этажа и положение его центра тяжести, 2-й Рамка Гульдина-это удобная методика расчета объема вращающегося тела(см. задачу 2.24). Задача 2. 22.На рисунке показана фигура корпуса баржи. С одного конца плоскости ADMSE и BCLTK, со стороны плоскости ABKE и DCLM, сверху с плоскости ABCD, определяют положение центра тяжести области однородной поверхности, которая ограничена вниз стороной полукруглого цилиндра. Обозначение: ADME и BCLK-равный квадрат со сторонами 2a, прямоугольник со стороной ABCD-сторона AB 10a. ось x%y, z показана на рисунке. один.
Решение. Вы можете видеть, что эта поверхность имеет ось симметрии в сочетании с z axis. So, центроид C в области этой поверхности находится на оси z и его 2 координаты xc, которые должны быть равны нулю. Поэтому необходимо определить только координату zc. Для этого мысленно разделите эту поверхность на несколько поверхностей так, чтобы было легко определить расположение центра тяжести в каждой из областей:1 и 2-квадрат ADME и BCLKb, 3 и 4-EMS и KLT. 5-прямоугольные поверхности ABCD, 6 и 7-прямоугольные поверхности ABKE и DCLMy, 8-полукруглые стороны EMSKLT.
Координаты центра тяжести zc определяемой площади поверхности н. Делится по формуле(2*):= -, в этом случае、 т. Ас. » L = 8 формат 8. Два *** 2 C = 8 — •0) Вычислить поверхность area. As*, 2, 8. Ч: Ас= АС2 = 4 <и Z3, Д 3 $ = Д 4$=, = As6 = как? = 20a2, & ss = = 10 r. a *. Тогда K = /,2,…Определены координаты центроида площади поверхности в точке 8, zh. Центроиды квадратов 7 и 2 находятся в их центре, то есть z \ = z ^ = A. В справочных данных о расположении центра тяжести некоторых однородных тел случай d) учитывался: d) центроид области кругового крепления находится на оси симметрии и разделен центром 2 греха — Круг на расстоянии, равном. Где r-радиус окружности. Об ОС ности, а-половина центрального угла. Для полуокружности 3
ВС ТК 2 грех-2 4 г = а, а= -.Итак, 0.03 = — ^- а-A, и координаты О 1 ТТ ой — 2 Полукруг 3, центр тяжести C3 равен z3 = OC3 = OOj 0 {C3 = 2e-i — » e = 2e(l + 2). So= ^ = + Центроиды областей прямоугольников 5, 6 и 7 находятся в их центре, то есть z6 = 0, z6-z — = a. Для определения координат z% от центра тяжести площади внешней поверхности полукруглого цилиндра используют случай c), который считается дугой однородной окружности.
Его центр тяжести находится далеко от цены Грех. Окружность расстояния jcc = r» — — -.Где r-радиус окружности, а A-половина центра angle. In в этом случае r = a, и 。Я… ТФ-ы, н-2-2 а = y. So 0] C8 = a — — — 1 = — a, и требуемая координата r8 Так… r8 = OC8 = OOi + 0, C8 = 2a + a = 2a ^ равно 1+^. Итак, при расчете площади отдельных участков этой поверхности и координат центра тяжести был получен следующий результат: Как,= ^ = 4 а \ ь $ = rAs4 = ^, АС5 = Асе = Как7 = 20a9; Подставляя эти значения в Формулу(1), получаем r = 1.35 a. То есть положение центра масс C в области этой однородной поверхности определяется координатами xc = must = 0, zc = l, 35a.
Задача 2.33.Твердое тело составлено однородного полого цилиндра / и высоты и, внутренний и внешний радиус дна равен К Р и г, однородный твердый конус ИИ дно радиус Р и высота Х. Веса материальных частиц Pk k-1 координаты прикладных точек xk, yk, zk определяются с точностью до размера частицы ego, поэтому эти формулы являются приближенными. Положение центра тяжести С твердого тела относительно частиц вещества не зависит от состояния твердого тела.
В дальнейшем рассматривается однородное твердое тело, в котором удельный вес всех материальных частиц постоянен. Координаты центра тяжести С однородного тела ХС, ус, zс примерно С. С. С. ХС = ^ нас= в 2 =(я ) К = Л к = [ Где & vk-объем материальной частицы k-W, xk, yk, zk-координаты точки действия силы тяжести этой частицы, V-объем н. Твердое тело: для повышения точности результата к => \
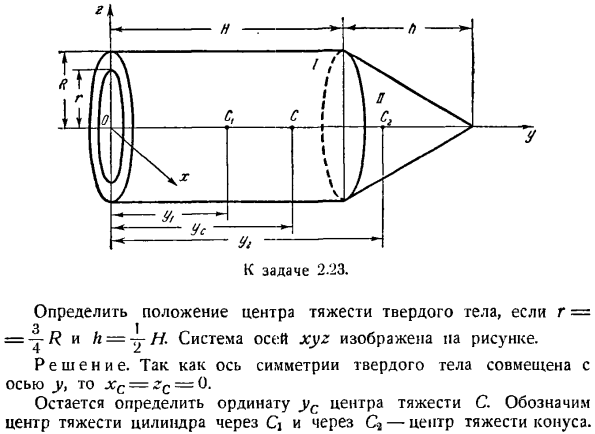
Подсчет необходим для того, чтобы разделить твердые частицы на материальные частицы в наименьшем возможном объеме. для r = 3 I определите центроидное положение твердого геля = — R и AYYA показывает систему осей xyz на рисунке. Решение. XC-zc-0-это потому, что ось симметрии твердого тела выровнена с осью Y. Остается определить ординату центроида C. центроид цилиндра равен C2, а центроид конуса равен C2. для расчета США используйте формулу (1).
в этом случае формат UM в 1 + Г * А<>*, Н AVi + Avf 9 1 ′ Где yx и Y) — ордината центра масс цилиндров A и B, A Ax / j и Lx; 3-объем этих тел соответственно. Мы это выясним: Д = — р *)я, = ыть=«, г, = н + \ н(2) (Напомним, что центр тяжести конуса C2 находится на расстоянии 4 минуты 1. по высоте от основания конуса). Используя соотношение(2), Запишите выражение (1)в виде: «те ( / ?>- Р2) У +(А+1 ч 1 я * » Л Г -• * Л 3 1. По условию и Λ= -//, это, наконец, выглядит так: 39 ″ Us = = 58
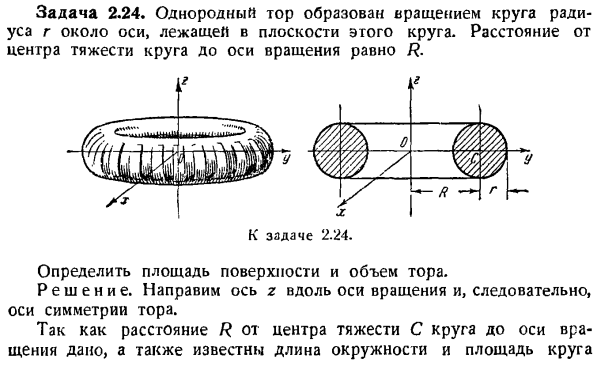
Таким образом, местоположение центроида с конкретного твердого тела определяется координатами. 39. ОКК = 0, ycz =〜ч, КЦ = 0. Задача 2. 24.Равномерный Тор образуется вращением окружности радиуса r вокруг оси в плоскости этой окружности. Расстояние от центра тяжести круга до оси вращения равно R. Определите площадь поверхности и объем Тора. Решение. ориентируйте ось z вдоль оси симметрии оси вращения, а значит и Тора.
Поскольку расстояние R от центра тяжести окружности C до оси вращения задано, окружность и площадь окружности также известны. Для радиуса r вы можете легко определить площадь поверхности и объем Тора, используя обе теоремы Гульдина. Фактически, согласно первой теореме Гульдина S = 2nycLt, yr-расстояние от центра тяжести линии, описывающей данную поверхность, до оси вращения, где L-длина этой линии, а 5-площадь поверхности вращающегося геля. В этом случае yn = Rt L = 2icr, следовательно, искомая площадь поверхности S Тора равна £= 2тэ /?。2Teg = 4Te2Hr.
Чтобы определить объем вращающегося тела, используйте 2-ю теорему Гульдина V = 2r. примените ycS. Где УГ-расстояние от центра тяжести С до центроида C до центроида C до центроида C до центроида C до центроида C до центроида C до центроида C до центроида C до центроида C до центроида C до центроида C до центроида C до центроида C до центроида C до центроида C до центроида C до центроида C до центроида C до центроида C до центроида с
В данном случае, уя = Р, tag3, и, следовательно, необходимый объем Тора, в В = 2 * /?Icr9 = 2 * V? Р9. Применение теоремы обоих Гульдинов оказалось весьма эффективным. Другие способы решения этой задачи, например, использование интегральных формул, являются более трудоемкими. Я… V. рекомендуется решить следующие задачи из «сборника задач теоретической механики» 1950 года и более поздних изданий Мещерского.286、287、289、292、293、295、296、300、302。
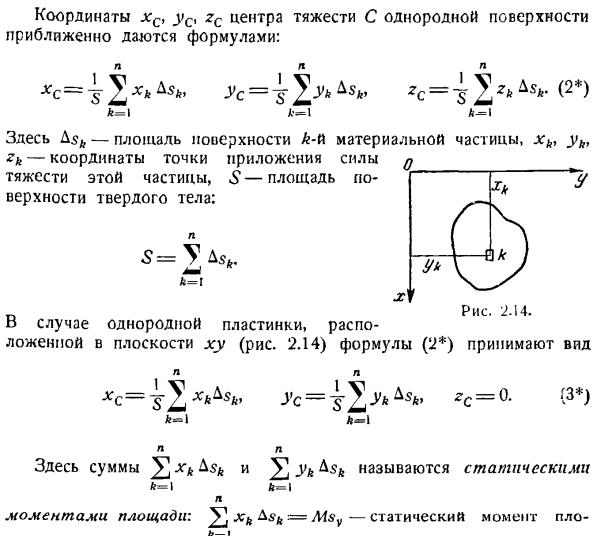
Координаты центра масс однородной поверхности xc, y0 zc задаются приблизительно следующей формулой: н. США = » Ы » КЦ =-5 2 ** ДжейТи = л в = 1 А-я Здесь площадь поверхности частицы вещества k-w, xk, yk, zk-координаты точки приложения силы тяжести q этой частицы, S-площадь поверхности твердого тела: н. Ы = г БСК. ч = я Икс _ 2.14 рис. для однородной пластины в плоскости XY(рис. 2.14) Формула (2 *)принимает вид: н = БСК, zс = 0.(3 *) фут-1 Где сумма^ xkbsk и^ Ык КСК называется статической к = \
Площадь момент:^&СК.= МСВ-статический момент б-я л. тень равномерного плана этажа относительно оси y,^ yk ^ sk == = Msx-статический момент площади однородного вида в плане относительно оси X. Если центр масс C однородного плана этажа находится на оси, то статический момент в области относительно этой оси будет равен нулю. Например, если центр масс C находится на оси X、 н. н. н. н. Компьютеры =£Ык БСК = 0.
Координаты xc, mustache и zc одноименного центра масс принимают примерно следующий вид: Где A / L-длина i-й материальной частицы, xkx yk-координаты точки действия силы тяжести этой частицы, а L-длина тела. л. (Пример: провод): L = ^если плоская кривая лежит в плоскости xy координата zc = 0. Если вы можете точно определить объем, площадь или длину каждой частицы и их центр тяжести, Формула(1 *)、(2 *)、(3 *)дает точное значение, а не аппроксимацию координат центроида всего тела.
Если приведенные выше значения не могут быть определены точно, то читатель, умеющий вычислять Интеграл, может воспользоваться приближенной Формулой(1 *)、(2 *)、(3 *)и вы можете использовать точные выражения вместо (4). а) однородный твердый корпус ХС = г ^ xdv по, МК =±^ ydv, КЦ = м \ здв,(5) (в) tVj их Где V = ^ dv (Интеграл распространяется на весь объем твердого тела Дого-Тай); B)даже поверхностный случай х ДС, МК = — \ — младший ярдов, КЦ = — г \ ЗДС(6*). 1($> а Где » S = ^ ds (Интеграл распространяется по поверхности твердого тела);
в) в случае четного плана этажа, расположенного в плоскости xy: XDS, и МК = ^ {м, zс = 0; (7 *) г)Для однородной линии ХС=] — \ xdlt МК =±\ ydl, КЦ=] — \ ЦДЛ,(8) (т (я)(я) Где L = ^ rf /(Интеграл распространяется по всей длине тела). <Си Если линия плоская и лежит на плоскости xy, zc = 0. Если однородное твердое тело имеет плоскость симметрии, то центр тяжести С находится на этой плоскости. Если тело имеет ось симметрии, то центроид находится на этой оси. Теорема Гульдина иногда используется для определения положения центра тяжести линий и площадей плоской фигуры.
Первая теорема Гурдина. Площадь боковой поверхности вращающегося тела (рис. 2.15) описывается плоскостью кривой (L / 3), она расположена в плоскости кривой, вращается вокруг оси (y), которая не пересекается с ней, и равна произведению длины дуги L на окружность 2jcc, которая описывается центроидом Рисунок 2.16. Так… _ «**7е-_ Г.- ::: Х \ А!〜 Рисунок 2.15. 2-я теорема гуруддина. Объем вращающегося тела (рис.2.16) описывается видом в плане, который расположен в плоскости этой фигуры и вращается вокруг ее контура и не пересекает ось (y), площадь фигуры равна произведению окружности, описываемой центроидом C, т. е. l / = 2nxcS.
Положение центра тяжести некоторых твердых тел простейших геометрических форм: а)центр тяжести однородной прямоугольной области находится на пересечении ее диагоналей; б) центроид площади однородного треугольника находится на пересечении его медиан. в) центр тяжести дуги однородной окружности(рис.2.17) находится на оси симметрии, ее расположение определяется координатами.
Смотрите также:
Предмет теоретическая механика
| Система сходящихся сил | Траектория и уравнения движения точки |
| Произвольная пространственная система сил | Скорость и ускорение точки |
