Оглавление:





































































Скорость и ускорение точки
- Точка скорость и ускорение Скорость точки-это производная по времени от положения r радиуса, которая определяет положение и пространство. Скорость точки характеризует изменение ее положения и времени ® = ТТ = с V ** + В + О. *) Вот, я, J, K-это ось. V, y, Z единичные векторы. Проекция скорости на ось фиксированных декартовых координат равна ДХ ды ДЗ. / G1AH 6) определите значения координат точек и любую константу интегрирования, используя момент nrsmspi. 7)
исключить время из уравнения движения и получить уравнение орбиты в координатной форме. Злое задание. , имел скорость v 8 км / С и цикл вращения T 1 час 36 минут, то есть 57 G0 секунд. Определите высоту полета спутника по поверхности Земли, предполагая, что орбита круговая и движение равномерное. Радиус Земли будет равен = 6370 км. Решение.
Первый спутник, запущенный в Советском Союзе в 1957/10/4 годах Людмила Фирмаль
Радиус орбиты спутника, проведенный от центра Земли, выражается буквой r, h x h — высота искомого спутника на поверхности Земли. Путь s, пройденный спутником за 1 Период вращения, равен произведению времени 7 «и расходуется на скорость v спутника, при 1 обороте, относительно выпуска 3.10.С другой стороны, тот же путь будет равен окружности радиуса R. Вт = 2-р、
Откуда? r = 7340 км. Мне. Далее найдите нужную высоту полета. ч = р-я = 7340-6370 = 970 км Задача 3.11. 2 точки перемещаются равномерно одна за другой По прямой линии с расстоянием между «скоростями» i, n и их начальным положением это было равносильно ок. Начались оба пункта. П3. Двигайтесь одновременно. А0 а. Определите время T. После этого 1 балл догонит задания 3.11, 3.12.
- Еще одна вещь. Решение. Линия ОС и траектория движения. Уравнение движения для первой точки, которая выходит из O, является: Уравнение движения для 2-й точки, выходящей из Oit, выглядит следующим образом: С. 2 = в ^ Т -| — А0、 Отчет о координатах все еще должен выполняться из начальной точки O. столкновение происходит в момент времени T. ол = а.3Т или v {T-v 0 = 0.
Пределы модулей скорости лодки с неограниченным увеличением во времени следующие: в — = Лим в = П. С. уз.- Задача 3. 16.Корабль движется в соответствии с уравнением, 0.055 / 50 тонн (1±.^ −0.055. / \ 1272.7 в — ’ М 50Т. Да.) The solution. To определите коэффициент скорости, вычислите абсолютное значение производной координат дуги относительно времени. _ _ O055 ^ 0i055 / 50 -■ 0.055 /•7 и> uij uyj- Да ДТ 1272.7 в.- 1 + 6е. 420___,, 0.055 / 1 + 6 * 0-0W / ■ Модуль начальной скорости судна определяется заменой t = 0 из(2). Версия v0 = 1У MjCCK. 50.(2)
Определите величину начальной скорости судна. Людмила Фирмаль
Задача 3. 16.Частицы, имеющие сухой заряд c, движутся в однородном электрическом поле переменной напряженности E = A $ \ r \ kt. Где A и K-постоянные коэффициенты. Форма уравнения движения частицы имеет вид Где t-постоянная. Определить величину скорости точки, ее начальное значение, а также максимальное и минимальное значения скорости. Решение.
Вычислите производную от x по времени, чтобы найти коэффициент скорости — (1-соѕ КТ). О, Боже мой. Тит-ТАТ. (1) Если мы подставим начальное значение времени£= 0 в уравнение (I)、 vQ = 0. Чтобы определить экстремальное значение коэффициента скорости, находим первую производную величины скорости относительно времени и считаем ее значение равным нулю, определяя время, за которое скорость достигает своего максимального и минимального значения. ДВ ДТ — Шин КТИ =0.м. В результате,//, = 0, r, 2n, 3ic,4zr, откуда Где ti = 0, I, 2, 3,… Подставляя значение найденного f в выражение(1), получаем следующее выражение: n-0 И если N = 1 (3) при последующих значениях n значения скорости(2)и(3)периодически повторяются.
Задача 3.17.Точка M движется по окружности радиуса r с постоянным тангенциальным ускорением, wv. At в первый раз точка была MQ, и скорость была равна нулю. Определите, в какой момент величина обычного ускорения будет представлять собой рампу тангенциального ускорения, и вычислите длину дуги, проходящей в этот момент. Решение. Равенство интеграции ДВ ДТ дифференциальный клапан. 1. \ > х = СГ (л) в w есть = const: vz = u> J + C, (2)
Где C — любая интегральная константа, определяемая из начального условия. Если /= 0, то подставляя эти значения в (2), т. к. C = 0、 В. = СШ. (3) Нормальное ускорение точки определяется по формуле _ ВЛ- ж * — р-р• Чтобы найти точку, в которой величины касательного ускорения и нормального ускорения равны, сделайте их значения равными Ж: Т \ Определите точку интереса Скорость точек(3) может быть представлена следующим образом:
При интеграции вы увидите следующее: с = м + с Постоянная C * определяется начальными условиями: для / = 0 a = 0. И затем… один. Предполагая, что I = tt в этом уравнении, мы находим искомое значение дуги. Вт. _гг — Т » — т- Задача 3.18.Нагрузка D подвешена на 2 кабелях£LS и / или BC, подвешенных на блоке BC. In исходное положение, отклоняющая стрелка ОС = с = 10 Дж / с л и АС = ВС. Расстояние между блоками Модуль скорости задается в Формуле в = в ^ + вл + вл. (3 *)
Направление скорости определяется направляющим Косинусом. потому что(<СХ).- =- J, а потому что(вты)=, потому что(<КЗ)= ВВ (4 *) Скорость является касательной к пути. Точка ускорения является производной по времени от скорости, но 2-й производной от радиус-вектора g относительно времени. Ускорение точек является мерой скорости изменения скорости. ^ В• * Й Я Щ w = dt = — Jr — = = W * 1 w> j Wzk ’(5)
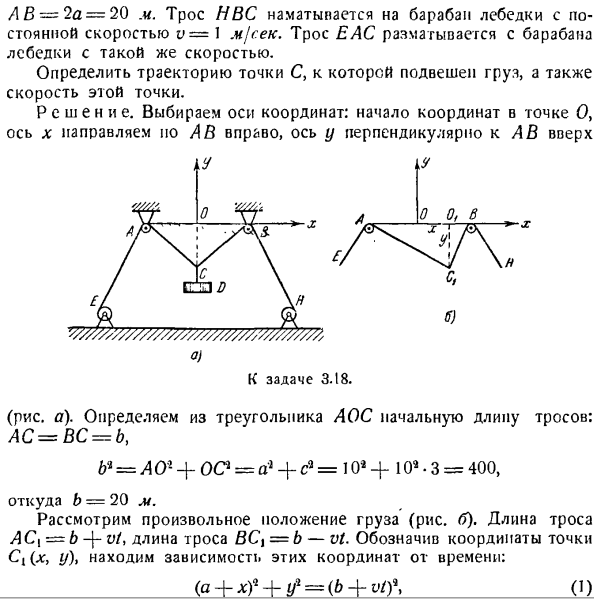
Проекция ускорения на неподвижную декартову ось с координатами раны ВХ = = Вайоминг-= г> вз = ^ з = ^(6 *) Коэффициент ускорения рассчитывается по формуле Вт—(- Вт и Вт «ручьи».(Г *) Направление ускорения определяется Косинусом направления. потому что («гдг)= -, потому что («0)==^, потому что(г * г)= ^. (8 *) Если уравнение движения задано в натуральном виде, то скорость точки равна LV = 2a = 20m. кабель NVS намотан на барабан лебедки с постоянной скоростью, v = I MjceK.
Кабель Эак намотан от барабанчика ворота на такой же скорости. Определите скорость движения этой точки, а также траекторию движения точки с, с которой будет подвешен груз. Решение. Выберите оси: начало координат точки O, направление оси x, где A B-это право, а y-ось перпендикулярна A B. Так… К заданию 3. 18. (Диаграмма а).Определите начальную длину кабеля от AOS треугольника. AC = BC = b、 Б * = АО * + ОС * = Д1-{- с * = 10 * + ж *. 3 = 400、 Где b = 20 м.
Рассмотрим произвольное положение груза(рисунок Б).Длина кабеля переменного тока \ = б — \ — Вт, длина кабеля БЦЗ = в-Вт. Если обозначить координаты точки C {(xy-y), то обнаружится временная зависимость этих координат. (а-х?+ я / =(б-Вт)(2) Если вычесть равенство (2) из (I), то оно выглядит так: х =■ ■ Вт = 2 /(3) проекция скорости в точке C на ось x выглядит следующим образом: Vv = x-и= 2 м! Ас./
Введем значение найденной координаты l: в Формулу(1)для определения временной зависимости координаты Y. < / = — //футов * — А2 + у—)А » = — [300-3 / а.(4) проекцию скорости на ось Y равна производной по времени от координаты Y V = 0 = 3t Vy U уже-37 «’ Скорость движения точек определяется по формуле в = Ви + Ви = 2И −1 — — ^ . * 1 1/300-3 * »
Модуль скорости «= ] Л + 300-С ’• Чтобы найти уравнение траектории движения груза, нужно решить уравнения (I) и (3) вместе и исключить из них время. После простого преобразования найдите орбитальное уравнение −1. Б * » Б * — В * — 1А Таким образом, груз перемещается по дуге овала. В решении этой задачи показаны различные методики составления уравнения движения а point.
In в этой задаче уравнения (1) и (2)представляют собой системы уравнений, определяющих временную зависимость координат, причем для каждой координаты они определяют уравнения движения (3) и (4) нагрузки. Задача 3. 19.Точка M согласовывается и вибрирует
Определить траекторию точки м. При значение S, траектория точки будет парабола? Найти скорость точки в первый раз. The solution. To определив траекторию движения точек, необходимо исключить время из уравнения motion. To для этого преобразуем первое уравнение следующим образом: х = а [потому что 2kt потому что г — (- 2kt грех грех е] = = а [cos9& / потому что е-sin1 КТ, потому что Е + 2 грех КТ, потому что КТ грех ЭЖ.
(3)из 2-й формулы, вы можете увидеть следующее: потому что = с \ Р \ КТ= -^\ -£. Подставляя эти значения в Формулу(3), получим формулу траектории движения точки M. Из уравнений(1), (2) видно, что для значений e координаты x и y не превышают rt a и±b, respectively. So, траектория ярма M вписывается в прямоугольник по бокам(2a и 26).Уравнение(4)является параболическим уравнением e,= 0 и e2 = (Приблизительно.
Определить скорость точки M. проекция этой скорости равна 1-й производной координаты, но время равно на VX = х == — ж грех (Мы), в = г—БК греха КТ. Установите / = 0, чтобы найти значение проекции первого момента. Я-ж =-2а / г Син э、 Итак, в первый раз скорость точки выводится из оси x, значение которой определяется по формуле (5).Задача 3.20.Точки движутся линейно в соответствии с уравнением x = 3 sin 2-t-4 cos 2gL.
Докажите, что движение точки является гармоническим колебательным motion. It определяет амплитуду и период вибрации. Найти скорость и ускорение точки Решение. Гармоническое колебательное движение определяется уравнением х = грех (КТ-(2) Или х = грех, потому что КТ(3-а потому что КТ грех С.(3) При сравнении Формул(1)и(3)、 k = 2^, cosЭ= 3, sin 3 =4.(4)
Из уравнения(4) можно увидеть следующее: *-25, или А-5. ТГ 3 = — я = 1.33,или P = 0.925. Подставляя значения A и^, найденные в Формуле(2), получаем: log = 1) sin(2 ^-0.925). Период колебаний равен Т = — = 1 секунда к Далее по направлению движения vx = x = 10 * cos(2r. t-0.925) найти проекцию скорости точки. Проекция точки ускорения равна = ЧХ = х = — 20т:9 грех(2rj-0.925)= — 4Л;.Задача 3.21.Приведено уравнение движения точки. Л ’= 2 + г].
Докажите, что точки делают гармонические колебательные motion. It определяет амплитуду, период колебаний, а также скорость и ускорение точек. Разрешены и Е. с использованием формул тригонометрии грех-=—(л-cos2n)、 Представьте себе тонкое уравнение движения. х = л-потому что(6 ^ + 1:) = 1 + грех + Из этого уравнения видно, что точка совершает гармоническое колебательное движение вблизи положения A, которое определяется в абсциссе X \ = 1 -.
Если вы переместите начало координат в точку A, уравнение движения для этой точки будет: х = грех(6 ^ — г]、 de x-координаты отсчитываются от точки A. амплитуда колебаний равна 1, периодичность T2tg _ 1 ■ 、 — tgCCK•к3 Проекция скорости точки ПА в направлении движения выражается формулой VX = = 6-cos +проекция ускорения точки равна Или Серии WX = 36ya’ — ЗБК ’ х. Задача 3.22.Точка перемещается в соответствии с уравнением s = 48 ^ — 4.
Где координата s измеряется в метрах, а время-в секундах. Мгновенно определите скорость точек (t = 1 сек, tl = 2 сек,^ s = 3 сек,£4 = 4 с ^ lg. Найдите среднюю скорость точек за 1, 2, 3 и 4 секунды. Найти среднюю скорость точек за 4 секунды: определить время и расстояние от начала трека в точке, где точка останавливается. \ e hi e n e. значение скорости определяется как производная пути по времени. = 48-12л(1)
Ввод значения времени в этом представлении говорит вам скорость. = 48-12 = 36 м / с,. я> Е3 = 48-12-22 = о、 fs3 = 4 8-12-3 * =-60 м / с, i> s4 = 48-12•4 * = −144 MjceK. Эти значения определяют величину скорости в определенной точке time. To определив среднее значение скорости, нужно разделить пройденное расстояние на период, в течение которого этот отрезок расстояния passes. So скорость первой 1 второй точки будет: si — от 44 до 0. 、 , = = — J — = 44 м / с、
Где координаты точки времени t = \ sec, S | = = 48-1 −4•i3 = 44 м, начальные координаты s0 = .- 0.In таким же образом определяется значение средней скорости точки за следующую секунду. ая, — ое, 64-44 в * СР =〜ifzrt ^ = С-и— = 20 Micefc> с — с-36-64 нет, y3cP = 7 ^ 77 = — [- =м / с、 ficp = 7 -?7 = — 1 — =-100 MlceK- Знак минус указывает на то, что скорость направлена в отрицательную сторону. Затем найдите точку, в которой точка остановилась. Это означает, что формула для скорости (1) равна нулю. 48-12 / 2 = О、 Откуда? t * = болезнь 2 секунды
V-В=: К = Б — (10 *> если «r»,> 0, то точка движется в направлении, в котором значение a увеличивается. для r » m 0 точка движется в противоположном направлении в направлении, в котором значение A уменьшается. Ускорение в этом случае определяется проекцией на естественную координатную ось.
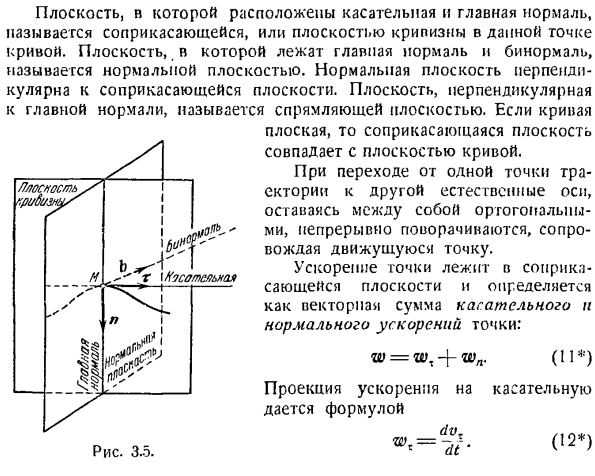
Естественная координатная ось, или естественное трехгранное тело траектории, представляет собой ортогональную (прямоугольную) систему координат, состоящую из оси/ 1. относительно а)/} она направлена на увеличение координат дуги, б)главная Нормаль направлена на вогнутость траектории, в) указанная/! Убедитесь, что 3 оси образуют правильную систему координат(рис. 3.5). В этот момент скорость точки равна нулю, а направление движения меняется на противоположное. =
При значении 2 секунды координаты точки равны s2 = 48•2-4•23 = 64 м. Время монотонно увеличивается, поэтому 2-й отрицательный маршрут должен быть отброшен, потому что он не имеет физического смысла. Определите среднее значение скорости за 4 секунды. Путь, по которому точка переместилась за 4 секунды, является суммой путей s * = 64.Путь переместился в первые 2 секунды, а точка переместилась в направлении отрицательной s в 3-й и 4-й секундах.
Этот метод заключается в следующем: при t = 4 s координаты точек были следующими: С4. 48•4-4•43 =-64 м. В результате на 3-й и 4-й секундах точка прошла путь / С4-С2 |-128 м. 4 секунды вообще, точка ушла далеко 64+ 128 = 192 м. Средняя скорость точек 192 lo, usr = — = 48 м / с Во-первых, следует отметить, что точка переместилась в сторону положительной оси s, и в этом направлении вдоль пути s5 = 64 м.
Затем точка переместилась на 128 м в противоположном направлении, а ее средняя скорость осталась постоянной по величине, и на этом участке пути была negative. As как видно из решения этой задачи, при определении средней скорости необходимо учитывать Если точка меняет направление движения точки, то необходимо учитывать тот факт, что движение состоит из всех движущихся участков пути, которые не могут быть равны разнице между координатами конца и начального положения точки.
Задача 3-23.Точка / VIt выбрасывается вертикально. Форма уравнения движения для точки при отсутствии сопротивления воздуха имеет вид х = х » (1) х. Где r> 0 и g-постоянные коэффициенты. Определяет скорость и ускорение точки, максимальную высоту точки и время, в которое точка достигает своего наивысшего положения. Решение.
Проекция скорости точки определяется как производная от временной координаты м> х = п-ГТ-(2) Проекция ускорения точки в прямолинейном движении равна производной проекции скорости времени или второй производной времени, отличной от координат Серии WX = = ЧХ = х = — г、 То есть ускорение точки является постоянной величиной. Из Формулы(2) видно, что ξ= 0 ’vx = vQ. Таким образом, константой является величина проекции скорости точки в первый момент.
Чтобы определить точку, в которой точка достигает максимальной высоты, используйте тот факт, что скорость точки в этом положении равна нулю. (2) указывает время нарастания через G. Поэтому время, когда точка достигает своего наивысшего положения, равно Т= -. (3) г в ’ Найти наибольшую высоту подъема h, подставив значение времени (3) в уравнение движения(1). для ВЛ ~ ~ 0 * 2 g * 2g ’ проблема 3.24.Mx точки, которые были брошены вертикально вверх с самого начала Скорость Zf0.
Через сколько секунд нужно подбросить Т вверх вертикально при начальной скорости 2-й точки с того же места Как обе точки встречаются в кратчайшие сроки от начала движения первой точки? уравнение движения то’ки подбрасывается вертикально вверх、 Отсутствие сопротивления воздуха икс= — Где v0-начальная скорость точки, А g-ускорение свободного падения. The solution. At на первый взгляд может показаться, что 2-я точка бросается одновременно с первой точкой.
Однако скорость 2-й точки очень мала, и к тому времени, когда первая догоняет ее, она падает на высоту Земли. Поэтому выбор момента во времени для приведения 2-й точки играет важную роль. 2-я точка Mit будет бросать вверх после того, как начальная скорость первой точки будет низкой t секунд, поэтому можно будет просто переместить первую точку обратно вниз. Давайте попробуем
Затем точка переместилась на 128 м в противоположном направлении, а ее средняя скорость осталась постоянной по величине, и на этом участке пути была negative. As как видно из решения этой задачи, при определении средней скорости необходимо учитывать
Если точка меняет направление движения точки, то необходимо учитывать тот факт, что движение состоит из всех движущихся участков пути, которые не могут быть равны разнице между координатами конца и начального положения точки. Задача 3-23.Точка / VIt выбрасывается вертикально.
Форма уравнения движения для точки при отсутствии сопротивления воздуха имеет вид х = х » (1) х. Где r> 0 и g-постоянные коэффициенты. Определяет скорость и ускорение точки, максимальную высоту точки и время, в которое точка достигает своего наивысшего положения. Решение. Проекция скорости точки определяется как производная от временной координаты м> х = п-ГТ-(2)
Проекция ускорения точки в прямолинейном движении равна производной проекции скорости времени или второй производной времени, отличной от координат Серии WX = = ЧХ = х = — г、 То есть ускорение точки является постоянной величиной. Из Формулы(2) видно, что ξ= 0 ’vx = vQ. Таким образом, константой является величина проекции скорости точки в первый момент.
Чтобы определить точку, в которой точка достигает максимальной высоты, используйте тот факт, что скорость точки в этом положении равна нулю. (2) указывает время нарастания через G. Поэтому время, когда точка достигает своего наивысшего положения, равно Т= -. (3) г в ’ Найти наибольшую высоту подъема h, подставив значение времени (3) в уравнение движения(1). для ВЛ ~ ~ 0 * 2 g * 2g ’ проблема 3.24.Mx точки, которые были брошены вертикально вверх с самого начала Скорость Zf0.
Через сколько секунд нужно подбросить Т вверх вертикально при начальной скорости 2-й точки с того же места Как обе точки встречаются в кратчайшие сроки от начала движения первой точки? уравнение движения то’ки подбрасывается вертикально вверх、 Отсутствие сопротивления воздуха икс= — Где v0-начальная скорость точки, А g-ускорение свободного падения. The solution.
At на первый взгляд может показаться, что 2-я точка бросается одновременно с первой точкой. Однако скорость 2-й точки очень мала, и к тому времени, когда первая догоняет ее, она падает на высоту Земли. Поэтому выбор момента во времени для приведения 2-й точки играет важную роль. 2-я точка Mit будет бросать вверх после того, как начальная скорость первой точки будет низкой t секунд, поэтому можно будет просто переместить первую точку обратно вниз. Давайте попробуем
Время, в течение которого первая точка перемещается с самой высокой позиции на встречу со 2-й точкой. Тогда путь, который спускался к первой точке во время tlt, был бы: s — ^ 1 — 2〜* Время от момента, когда первая точка находится в своем наивысшем положении до момента, когда 2-я точка начинает двигаться, представлено Z. затем путь до 2-й точки достигает первой точки Два С. 1 = ВЛ(м-х)
В момент tx точка была заполнена, поэтому、 Си + Си = ч,(1) Где h-наибольшая высота первой точки и равна v% j2g (см. предыдущую задачу).Затем, подставив значение (1) всех величин, можно увидеть следующее: Если мы рассматриваем это уравнение как неявную зависимость tl — /(x), мы находим производную tx относительно m, приравнивая эту пулю. ДХ фдж ГЗ Откуда? Ho Vi / g равно времени подъема 2-й точки На наибольшую высоту (см. выпуск 3.23).
Поэтому на момент встречи 2-й пункт будет самым высоким. Назначьте найденное значение tx- (3) Формуле(2).Затем, когда вы бросаете такой член, вы видите следующее: л. 2г-2-т-2г> Где назначенное время 1.• Тл == Тогда из Формулы(3)можно увидеть: — Ви + yvT-в * £ С момента броска первой точки необходимо поднять 2-ю точку, после чего, чтобы найти требуемое время моль, необходимо добавить время t0t, при котором первая точка достигнет наивысшего положения. Дж г 1 г Из Формулы(4)、 для R М> 0″5> 2р;}, для M = 0 ИС и ВН = 2В-в、
Поэтому, если вы бросаете 2-е очко、 Как первая точка достигла наивысшего положения? Когда 2-я точка брошена, прежде чем первая точка находится в своем самом высоком положении. Также, если m = 0, то 2-я точка выбрасывается в тот момент, когда первая эструс находится на самом высоком уровне. Задача 3.26.Линии ellipsography АВ = 1 слайды заканчиваются на горизонтальной оси, а конец Б по вертикальной оси. Вам будет дана линейка Да.
Задание 3.25 к. Кривошип закреплен шарниром посередине, в движении по ОС = 0,5/.Расстояние AM = ay VM = b известно. Угол<Р между горизонтальной осью и кривошипом изменяется пропорционально времени г = КТ. Найти уравнение движения и уравнение траекторий для точки M эллипсографии. Также определяют радиус кривизны траектории точки M, любое положение механизма, в частности время t {= 0 и T = MC / 2k при скорости, касательной, нормальном и полном ускорении. The solution.
To составим уравнение движения точки M, рассмотрим треугольник OAC. It является двудольным: OS-AC = 0.5/, следовательно,£СОА = ^ CAO = y = KT. Тогда координаты точки A1 выглядят так: х = БМ, потому что СР = = Б, потому что КТ(1) y = zAAi sin 9 = a sin kt, (2) Или в векторном формате Р = ХІ-{- ый = Б, потому что Т-Я—Грех КТ•Ят Где i, j-единичные векторы осей x, Y. Эти уравнения определяют уравнение движения для точки M. Чтобы найти траекторию движения точки, представим уравнение движения в виде x. = потому что КТ = КТ грех, а
Добавьте эти уравнения, возведя их в квадрат. Б3 ′ Итак, геометрическое место точек м есть полуоси б, эллипс А. Чтобы определить скорость точки M, вычислите 1-ю производную координаты относительно времени, равную проекции скорости точки на соответствующие координатные оси. ЧХ = х = — БК греха kty вы = ыть = Ак, потому что КТ. Величина скорости определяется по формуле в = в Ви + х * = к глаг * sin2 т-ф а * cos2 КТ. (3)
Косинусы направления векторов скорости являются: _, Г4 ч ЧХ-б грех КТ в COS(V, х)= — х — = В sin2 л / cos8 Фе / ’ В Дж / б * Син кт + до TI2 потому что * КТ ’ В векторном виде скорость может быть представлена следующим образом: v = vj-f-Vyj—bk sin kt•I-f-Q-k cos kt * j. Найдите проекцию ускорения на координатных осях и вычислите 1-ю производную по времени проекции скорости или 2-ю производную по времени координаты точки. WX и = я)х = — ЧД * потому что kty Вайоминг = уу = г = — Ак * грех КТ. (4) Величина ускорения определяется по формуле Вт = Фольксваген%+ зо * г = klVP потому что * кі + в * грех * КТ.
Направление ускорения можно найти путем сравнения уравнений движения точек(1), (2) и Формулы (4), определяющей проекцию ускорения на координатные оси. Последний может быть представлен следующим образом Серии WX = — к * Х, Вайоминг—№у\ Подобный этому Вт = wxi по — \ — Wyj = — (си 4-ый)= — К-Р. Плоскость, в которой расположены касательная и главная линии, называется плоскостью контакта или плоскостью кривизны в определенной точке кривой.
Плоскость, в которой присутствуют главные нормали и бинормалы, называется нормальной плоскостью. Нормальная плоскость перпендикулярна плоскости контакта. Плоскость, перпендикулярная главной линии, называется плоскостью выпрямления. Для кривых Если она плоская, то плоскость контакта совпадает с плоскостью кривой.
При перемещении из одной точки траектории в другую естественные оси, остающиеся перпендикулярными друг другу, непрерывно вращаются вместе с движущейся точкой. Ускорение точки находится в плоскости контакта и определяется как векторная сумма тангенциального ускорения и нормального ускорения точки. ж = ж,-\ — шя. (11 *) Рисунок 3.5. Касательная К Проекция ускорения задается формулой дифференциальный клапан. (12 *)
Так, ускорение точки M направлено вдоль радиус-вектора, проведенного от M до O, но величина его прямо пропорциональна расстоянию точки M от начала координат. Проекция ускорения по касательной определяется как производная проекции скорости по касательной во времени (в данном случае vt = v). Вт dy к *(Б ^-А3) грех КТ, потому что КТ ДТ-гг sin2-т м — C0S * Ят ’ Величина Ho, суммарного ускорения связана с касательными и нормальным ускорением зависимостями П1 = ш \ ш%.
Теперь, после простого преобразования, существует значение нормального ускорения точки M: ЗП = Р =,(5) А9 сов * т б * sin8 КТ Найти радиус кривизны орбиты, зная нормальный коэффициент ускорения точки (5) и ее скорость (3). Я… в * (А2 cos1 КТ-Ф — Б’ 1 sin2 Т)* ^ шя АБ Используйте полученную формулу для определения основных импульсов в любой момент времени и выясните их значения: КТТ = 0 Х б 0. 0. Akj-БКИ в 0 0 k. b. k’Q. ж-к-бл-к * АФ Б * я б * задача 3.26.Кривошип OL = g равномерно вращается вокруг точки O плоскости чертежа: угол y = kt.
Шарнирный шарнир АВ соединен с концом кривошипа в точке А и проходит через цилиндрический шарнир, который может вращаться вокруг неподвижного центра L/.Длина AB = 1 ^>(2d. Уравнение движения точки в, проекция скорости и ускорения на координатные оси, касательная линия, нормальное ускорение, суммарное ускорение, а также определяют радиус кривизны траектории любого положения механизма. определите координаты точки B при cp = 0 и cp = r, скорость, ускорение и радиус кривизны ее траектории. Решение. Поскольку OA = ON = r, треугольник OAN равнобедренный. Поэтому Оан = О. Я! = 90° —
я = ^ — <- и р » — р S-грех?〜 /. ’-ОН- КУ КУ + ^ — Р / см-дж-дж С другой стороны, нормальное ускорение е Отсюда вы знаете скорость точки и нормальное ускорение, поэтому вы можете определить радиус кривизны. ! + Р—\ РЛ грех ^) П » В、
Приступаем к расчету скорости и ускорения по координатам точки B, угол(4g2 + / d) 2 Нормальное ускорение Po-8r — * / • * в соответствии с углом<pi = » эти величины равны Икс (Да ХІ = — г+/, ух = о、 ТК’.j. Ах.、 Р » —О -’ (2г -/) 3 Задача 3.27.Точка M, движущаяся с постоянной скоростью v, представляет собой цепную линию, форма которой равна Правильно. Но… ^ = о.)
Определяет проекцию скорости и ускорения, а также полное ускорение точки в зависимости от координат. Определите радиус кривизны драгоценной линии. Примечание используйте уравнение гиперболической функции с экспоненциальной функцией. сл \ 2 = Г (Э-э〜*) т ч з = с — J (ех + е〜з) Т ♦У 2 е 2 = — р—. ч 2 Решение. Если мы примем во внимание X и y, где мы вводим уравнение цепной линии как функцию времени, и мы дифференцируем цепную линию по времени: Рий (х \ … икс.,. К задаче 3.27.
Кроме того, поскольку сумма квадратов проекции скорости равна квадратам скорости точки、 г * = В1-х (3) Если взять уравнение (2) в степени 2 и подставить его значение(3) вместо левой части, то получим: в ^ — Х ^ р-ш — (4) Но… Или Л — — — т — » — ВР * Я J-slis не-ЧС-1 а Извлечь квадратный корень из обеих сторон уравнения(5) можно легко * V <1 / g \ •(6> Вот оно.
Равенства определяют проекцию скорости оси абсцисс в зависимости от координат точек. чтобы определить проекцию скорости на ось y, подставим значение (G), найденное в Формуле (2).И затем… ва. икс м- — — ш -, (7) 7 лет » Или, если вы введете значение y в (1)в это уравнение, вы можете увидеть, что: П = ±ВТН. (8) Чтобы рассчитать проекцию ускорения на ось абсцисс, дифференцируем зависимость (6) со временем, помня, что v = const. ва. ва ва. x v-a9, x / Лига Чемпионов х = — г — — — й * — Ш— — — — — Г-ш -. (9) У3 * у у У3 а в 7
Чтобы определить проекцию ускорения на продольную ось, вычислите производную 2-го порядка по времени в продольной координате с помощью (8). Р = — ВФ (10) СН2-с Учитывая (G), узнайте ниже. в ВА В * А9 / 11н гл’^ Но… Чтобы найти ускорение точки, используйте следующую формулу ж * = 1п-+ — У3, (12) Тангенциальное ускорение характеризует изменение величины скорости. Если величина скорости не изменится, то она будет равна zero.
In кроме того, он исчезает, когда скорость достигает экстремального значения. Нормальное значение ускорения определяется по формуле Где P-радиус кривизны траектории. Нормальное ускорение характеризует изменение скорости direction. In в обоих случаях радиус кривизны бесконечен, поэтому он равен точке перегиба пули и траектории линейного движения пули. point. In кроме того, обычное ускорение исчезает в точке m> = 0.
Коэффициент ускорения рассчитывается по формуле Вт = В ^ + ^ К = +(Джей-Джей.(14 *) Направление ускорения определяется Косинусом направления. потому что(ш? х)^, потому что(МАС Н)=(15 *) После простого преобразования подставим (9) и (11). 2 ТВ-А2 \ {,,. о Х \ Фольксваген, о Х / 10ч Яг = — ч 1 4-СЛР -} = — м-ч -. (13) \ J В\и} V Если вы снова используете равенство (I) и извлекаете квадратный корень из (13), вы найдете значение ускорения точки. (14) г-в. Из-за этого условия точка движется с постоянной скоростью, поэтому максимальное ускорение одновременно является и нормальным ускорением. О3 / 1GCH з = ЗП = Дж. (15)
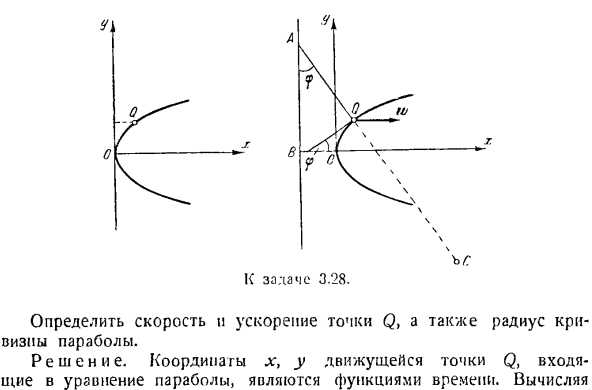
Определите радиус кривизны цепной линии, сравнив равенства (14) и (15) р = 4-(с) Эта задача может быть решена путем прямого дифференцирования уравнения цепной линии без передачи его в гиперболическую функцию. Однако это решение будет более длительным. Задача 3.28.Поскольку точка Q движется вдоль параболы y2-2px, положение проекции на продольную ось задается уравнением y = ct. K * выпуск 3.28.
Определите скорость и ускорение точки Q, а также радиус кривизны параболы. Решение. Координаты X и y движущейся точки Q в уравнении параболы являются функцией time. By вычислительная техника с. 0. \ Производные по времени с обеих сторон параболического уравнения、 2У = 2 пикселя Или yvyбыл = данные. (1) С другой стороны, если мы дифференцируем по времени y = ct}, мы можем видеть, что: Р = уу = С. Тогда из (1): Зет. х р ’ Поэтому скорость точек определяется соотношением v = = 1(2)
Предсказание ускорения осей координат может быть получено с помощью следующего уравнения. С2 и> х = = — г = Дж = const и、 Вайоминг = ты = 0. Таким образом, коэффициент ускорения абсолютной точки равен С2 Вт = WX с Я я =-. Если обозначить угол между касательной параболы и осью x буквой В * _ _ _ _ в * п Откуда? Рассматривая P wn W j siri ’f F C2 I Sin cp j’ или(2), получаем следующее: Р =(3) Р / Син? Мне. в’ Восстановление в точке D на расстоянии OB = p / 2 От точки о перпендикулярно оси абсцисс(направление параболы)
Найти точку A, где этот перпендикуляр пересекает pores. It меньше, чем траектория точки. И затем… / ОБЕСПЕЧЕНИЕ КАЧЕСТВА.- =|- G. (4) 1 ^ 1 | грех ’ Ф | Если сравнить равенство (3) и равенство (4), то можно увидеть, что: ? = \ \ КК = 2 \ ОК \、 Где точка С является центром кривизны. Задача 3.29.Точка Л1 движется по уравнению<z = aek’, а uyl, образованный полным ускорением по касательной, не изменяется и равен 60°. Определите скорость точки, касательную линию, нормали и общее ускорение, а также радиус кривизны траектории в зависимости от дуги Z. Решение.
Проекция скорости на касательную определяется как производная по времени дуги ВЗ = б = akek: = АА. Проекция точки ускорения от касательной равна、 ш — я). = Ак * ЦКТ = олр. Поскольку угол между идеальным ускорением и касательной известен по условиям, абсолютный модуль идеального ускорения определяется из уравнения Вт соѕ а = у \ Откуда? cosı) Величина нормального ускорения точек выглядит следующим образом: ЗП = МК * — = зл-это радиус кривизны траектории определяется по формуле К заданию 3.29. | / 3 К * с Ли 3. __ ВГ. 3. Радиус кривизны увеличивается бесконечно со временем. Траектория движения точки представляет собой ветвь спирали.
Задача 3.30.Движение точки задается уравнениями декартовых координат х = с * Косинус Т, Г-Ц (тая греха ми.* Определяет радиус траектории кривой. The solution. To найти радиус кривизны орбиты, используя формулу ускорения пор О Рассчитайте скорость точек. Проекция скорости pa равна фиксированной декартовой оси радиостанция VX = х = е (потому что Т-Син т)> вы = Г = Е ((потому что Т греха т \ с V2 = я•= — В * = Е ’] / Т р х » г » г Определите проекцию ускорения точки. серии WX = х = — 2С {греха Т гор = г = 2эц потому что Т, вз-з-Эл.
Абсолютное значение ускорения равно Тангенциальное ускорение определяется как производная скорости по времени. Найти его нормальное ускорение, учитывая максимальное ускорение точки и величину касательного ускорения В2 = ш \ — [- з-н -、 Откуда? Вт н = ж * — ж \ = УО *-?> ЕV = 2е# Следовательно、 ЗП = Эль г л \ Введите значение скорости и нормального ускорения в Формулу(1), и вы увидите радиус кривизны траектории ()= ’-= −7-= ТГ-В-2 *. (3) Радиус кривизны и нормальное ускорение являются важными характеристиками движения точки.
В этой задаче из Формулы (3) видно, что за счет неограниченного увеличения времени радиус кривизны увеличивается бесконечно. Однако, как видно из (2), нормальное ускорение не стремится к нулю при неограниченном увеличении времени, а, наоборот, увеличивается без неограниченного количества времени.
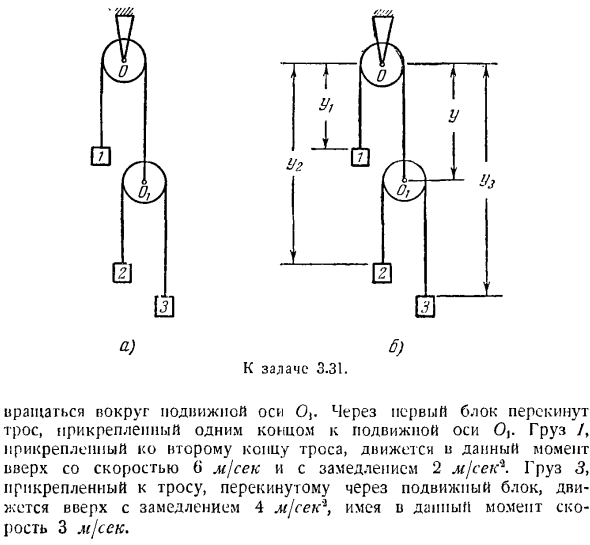
Траектория точки, определяемая параметрическими уравнениями движения, представляет собой логарифмическую спираль, радиус ее кривизны бесконечно увеличивается со временем. Задача 3.31.Система состоит из 2 блоков(рисунок а), 1 может вращаться вокруг неподвижной оси О, а 2-й Один. м. т. Так… Я… Так… □ Да. □ Узу В 0. в б.) один.) Крейс 3.31. Вращающийся вокруг подвижной оси o трос, прикрепленный к одному концу подвижной оси O, перекидывается через первый блок.
Груз, прикрепленный ко 2-му концу троса, теперь движется вверх со скоростью 6 м / с с замедлением 2 м / с.Груз 3, установленный на тросе, подвешенном на подвижном блоке, движется вверх с уменьшением на 4 м / с, и в данный момент он составляет 3 м / с. Важным частным случаем движения является движение равномерное и колеблющееся equally. In равномерное движение, скорость постоянна. Уравнение движения с постоянной скоростью о = о о + ви,(16 *) Где o — координата дуги точки, отсчитанной от начала координат, а o0-значение координаты дуги в точке/=.
При равном знакопеременном движении тангенциальное ускорение точки является постоянным по величине. Уравнение равного движения выглядит так: ^^ ОРВ + ^ Ф. Клеммник (J7 *) Зависимость времени от движения, при котором скорость изменяется равномерно, определяется уравнением на VX = v0 в + СШ. (18 *) Если перемещение определяется уравнениями (17 *) и (18)、
Если это движение равно, то оно будет равномерно ускорено Медленно двигаться (^^> 0). в общем случае при ускоренном движении тангенциальное ускорение совпадает по знаку с проекцией скорости по касательной direction. In при замедленном движении существует знак, противоположный касательному направлению ускорения и проекции скорости на касательную. Соотношение между скоростью и расстоянием, пройденным равными чередующимися движениями, определяется формулой Галилея И что? = вл + 2wx(о-ц0). Часто задача заключается в нахождении радиуса кривизны траектории. Р
адиус кривизны траектории можно определить по формуле (13). В V2. Р = 1 -. (19 ) Найти скорость и ускорение центра движущегося блока, точку Oi, удельную временную нагрузку 2. Решение. Порядковый координата груза показана на буквы Г, ый, ый, и точку o (рис. 6). ’Длина кабеля между нагрузкой Y и центром блока Oj остается неизменной、 Г \ «лы-Т-константный、 Где буква R обозначает радиус блока. Аналогично, длина кабеля, соединяющего нагрузку 2 и 3, одинакова. Представляет длину этого кабел
я Если вы различаете оба уравнения Uch-Y » Uz-y — \ — zr = const по времени, вы можете видеть, что: )> 1-hL-2 > > = 0. Если подставить указанные значения I-speed px и ul, то получится: если мы получим дифференциальное уравнение (1) относительно времени p =-6 m j секунд,= — pa =-15 m /s, то: Йи + Дж? а-2Д)= 0 Вводя известные значения ускорения yx в эти уравнения, мы видим, чт
о: y = 2 м / с, = 2y-Z’Z = 8 м / с . Таким образом, скорость#и ускорение в точке Ox равны скорости и ускорению груза/, направленного в противоположную сторону. Скорость движения груза 2 Пи равна 15 м / с в направлении вниз, а ускорение этого груза равно 8 м / с в направлении вверх Задача 3.32.Ускорение точки составляет 12 ТМ-сек. оно направлено в отрицательном направлении вдоль оси v. t =(через 2 секунды скорость точки была рав
на b М / с, направленной в положительном направлении вдоль x-axis. AT t= 3 секунды, точка находилась на оси Х на расстоянии 50 м от исходного положения. Определите уравнение движения точки. Решение. Поскольку точка движется линейно вдоль оси x, ускорение проекции на ось x равно
Это уравнение выражается в следующем виде поразил =-12 / » ДТ (я) Умножив обе части на dt, заметим, что _ dj Д ^ х DT * ~ ~ ДТ ’ Формула (1) для интегрирования. л ’= — «’ + с,. (2) Чтобы определить любую интегральную константу C, используйте условие{t = 2 секунды и x = 6 м \секунд. Если ввести значения этих п
еременных в Формулу(2), то можно увидеть следующее: Г =-6•23 + М Или С,= 30. Уравнение (2)принимает вид §ВБ/ * 4з. Если мы умножим обе стороны этого уравнения на dt, это выглядит так: ДХ =-60 ДТ 30 ДТ. При интеграции вы получаете следующее: л- = −2 / ’ — (- 30г + с *.(3) Любая интегральная константа C! Для определения T введем в Формулу (3) условие n = 50m для каждой F = 3 секунды. 50 =-2•27 + 30•3 +Съ Отсюда С,=И. Введите это значение в уравнение(3)и вы найдете уравнение движения для точки * = −2/3 + 30 / — f 14. Задача 3. 33. В течение 20 секунд скорость судна, движущегося (циркулирующего) по дуге радиусом 200 м, падает с 15 до 12 м / с. Предположим, что величина тангенциального ускорения пропорциональна степени 2 скорости,
и определим nyib и круговой угол, пройденный за первые 10 секунд. Решение. Так как тангенциальное ускорение корабля пропорционально мощности 2 скорости、 — =\КВ(1) Где h-коэффициент пропорциональности, величина которого неизвестна. Когда вы изолируете переменную, вы видите следующее: дифференциальный клапан. виджей. Чтобы найти коэффициент k, воспользуемся условием, что в течение 20 секунд скорость судна падает с 15 до 12 м / с. Если проинтегрировать уравнение (1) в этих пределах, то оно выглядит так: 11, 10. И
ли 15. 12. _ _ _ В. = 2 0 / г、 Откуда? 12 \ 5〜 1/1200. Кроме того, определите траекторию, по которой двигался корабль в первые 10 секунд. Для этого сначала (1) Находим по Интегралу от скорости как функции времени. У нас есть: —- С = КТ. (2) В. Чтобы определить любую интегральную постоянную, нужно использовать начальные условия движения: для = = 0, скорость v = vQ. Если ввести значения этих переменных в (2), то можно увидеть следующее: с= Присвойте это значение(2), чтобы определить скорость год= 1—v0kt• Найти длину пути, по которому корабль прошел за п
ервые 10 секунд?!Используйте клавиши со стрелками для перемещения. Зависимость ДС _ ВН При объединении переменных в изоляции можно увидеть следующее: ДС = Откуда? Ю. Ю. _ dvnt _ _ К-Д (- подойдя к) } Я-vjtt ЮА л-КВ * Т Так… 10. 5 = — Ifl (1-kv0t) При замене значений для всех величин, вы получите следующее: ы = 1200 в(1 + 1 / 1200-15-10) = 1200 в 9/8 ^ 150 м П
осле этого угол окружности в радианах выглядит так О = З / Р = 150/200 = 0.75. Задача 3.44.Движутся линейно с ускорением Вт = 6 Дж Где находится координата point. At время tx = 2 секунды, координаты точек равны lg | = 27 м, скорость равна = 27 м \с Уравнение движения точки и определяет временную зависимость скорости и ускорения. The solution. To найти уравнение движения точки, заданная зависимость ускорения от нуги выражается в виде: Умножьте обе стороны уравнения на dx, чтобы разделить переменные ДХ-ДВ _ я Р-и-Т =-6 WX с дх、 Откуда? ВК-IV—(QX в] / 3
ДХ. При интеграции вы увидите следующее: £°* 4 / 3_С»(1) C — любой Интеграл constant. To определив его, подставим значение m> 1 = 27 м / с в уравнение (1) с^ = 27 м. Затем получим C,= 0 из Формулы (1)、 в = 3х’2 / 3. (2) Используйте зависимость v == dx / dt и умножьте уравнение (2) на dt, чтобы разделить переменные = 3 ДТ. Х2’3. т. Да.) б.) К выпуску 3.35. При интеграции вы увидите следующее: Bx1l = В4-с *(3) Используя условие задачи, опр
еделим произвольную интегральную постоянную: for = 2 sec ^ 1 = 27 m. подставляя эти значения В Уравнении (3) Найти C9 = 3.Получим уравнение движения для точки и подставим значение любой константы в (3).* = < / + \)\ найти временную зависимость скорости, вычисляя производную по времени от x. v = 3(/ + 1)’. Ускорение как функция времени определяется как производная скорости по отношению ко времени. Вт = 6(Т + 1). Задача 3.35.Временная зависимость расстояния перемеще
ния определяется трапецией, показанной на графике. Создайте график, представляющий временную зависимость величины скорости («?»).4 = $.). Решение. В течение периода от 0 до tx точки перемещаются равномерно с той же скоростью, что и абсолютные значения Момент tx от T. до x, точка фиксирована и расстояние от начала пути не изменяется. Дал
ее, от момента tt до момента m <ment tz, точка равномерно движется в противоположном направлении со скоростью, равной абсолютному значению. В. На рисунке показана временная зависимость требуемой скорости. один. Задача 3.36.Временная зависимость скорости первой точки представлена дугами полукруга АМВ. Отправная точка
Если уравнение движения задано в декартовых координатах, то уравнения(3 )и(7) следует использовать для нахождения величины скорости и ускорения точки, а также величины тангенциального ускорения по формуле (12).Затем из соотношения (14) определяется обычное ускорение, а далее(19*) используется радиус кривизны траектории. Если точка движетс
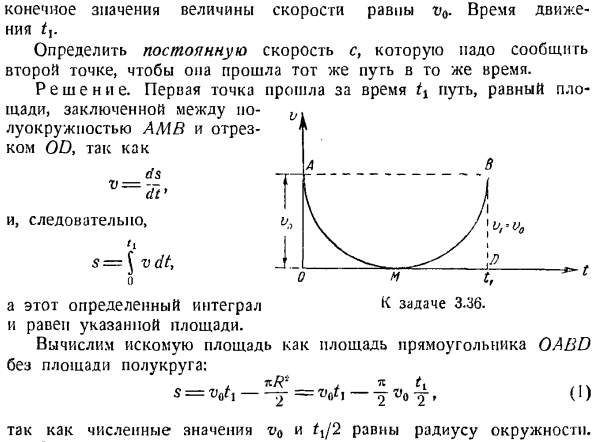
я по плоской кривой, то радиус кривизны траектории и нормальное ускорение точки можно определить другим способом. Буква f обозначает угол, под которым тангенс локуса (или эквивалентная скорость) формируется в постоянном и неизменном направлении (рис.3.6).Тогда радиус кривизны Конечное значение скорости равно Определите постоянную скорост
ь c. это должно быть сообщено во 2-й точке, чтобы двигаться по тому же пути в то же время. Решение. Первая точка прошла путь, равный площади, заключенной между полукруглым и OD сегментами AMB в момент времени tx. И эта определенная интегральная задача к 3.36.Равна указанной площади. Требуемая площадь рассчитывается как площадь прямоугольника автономной адресной книги, исключая площадь полукруга. S=: VQt, — j = V0t}—J v0(I) потому что цифры в v0 и TX / 2 равны радиусу окружности. С другой стороны, потому что 2-й пункт должен также продолжаться в то же время、 ы =(2) Если вы выравниваете значения обоих путей (1) и (2)、 А к ти、 Если скорость 2-ой точки равна с = ВБ \
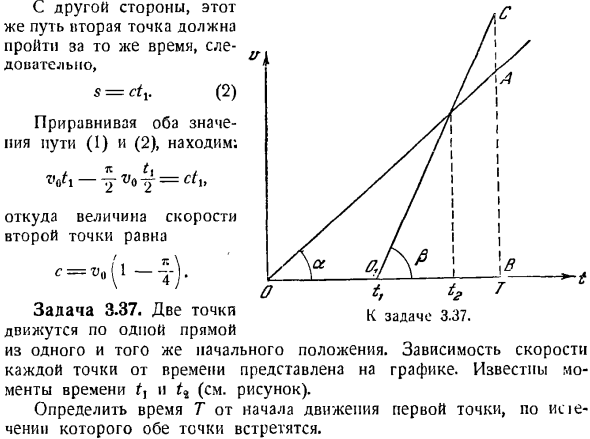
л- Задача 3.37. 337 указывает на проблему 2< Двигайтесь по прямой линии Из той же исходной позиции. Временная зависимость скорости каждой точки показана на графике. В момент времени F(см. рисунок). Определить время t от начала движения первой точки. Исходя из этого, обе точки совпадают. Решение. Площадь треугольника автономной адресной книги, в которой первая точка времени t численно равна пройденному пути, задается формулой: ±Обь-АВ =±Т. Т. ТГО. Где а-угол наклона прямой ОА относительно абсциссы. Площадь треугольника 0 {CB, числ
енно равная / к пути, по которому 2-я точка перемещалась одновременно, представляется следующим образом: l201B. КБ = ли (Т-Тл) (Т-Тл) ИГ% Где p-угол наклона прямой 0 \ C относительно абсциссы. Точки совпадают на 7″.в этом случае Нуга будет equal. So, если мы сделаем площадь треугольника равной численно перемещенной траектории, то она будет выглядеть так: \ =(Я) С другой стороны, уравнение выводится из графика Я » = (я-я) тг?。 (2) Решите систему уравнений(1) и(2).Из Формулы(2): 1 г> Ф Г5 я Подавите значение ego выражения(1) и после простого пр
еобразования уменьшите обе стороны уравнения на tgp. м ^ у-Гуш). Задача 3.38.MAPIC также представляет зависимость величины быстрого ввода или времени от 2 линейно движущихся точек, появляющихся одновременно из одного и того же места. Временная зависимость модуля скорости рисуется на графике первой точки линии, проходящей через начало координат, вторая точка-окружность. И так далее. Определение: 1) у
скорение 2-й точки как функция времени. 2) ускорение первой точки, если мы знаем, что первая догонит вторую точку и второй момент, который остановит гомосексуалиста в конце. 3) Расчет времени К выпуску 3.38. Начало доения до того момента, когда скорость обеих точек будет равна. считайте, что v0 и tt известны. Решение. Рассмотрим любое положение 2-й точки АФ, которое занимает в некоторой точке Т(рис.6). 1.Отрезок MN равен коэффициенту скорости vly во 2-й точке, а отрезок ON соответствует времени t. радиус OM, с одной стороны, равен начальной скорости vQ}2-й точки, А с другой стороны, времени tu, в которое о
станавливается 2-я точка. И затем… В.® т. что-то, грех=. во-Г1 если упорядочить и добавить в квадрат 2 уравнения Эгиды, то можно увидеть следующее: Ту \ 4、/ / Поэтому коэффициент скорости 2-й точки в любой момент времени равен Проекция ускорения 2-й точки, которая движется по прямой, направление движения выглядит следующим образом. = я)<я =- L Vi \ — t’R 2. 2-
й пункт останавливается at=.In другими словами, путь, по которому перемещается 2-я точка t = tv, измеряется площадью 1/4 окружности 4 = Оми-Оми ^^ Vi- В то же время первая точка для ускорения перемещается в то же время Где W \ — искомое значение ускорения первой точки. В зависимости от условия, путь, по которому обе точки были перемещены в этой точке, будет равным. Это потому, что в этот момент первый догонит второй. Следовательно,=и Отсюда определяется коэффициент ускорения первой точки
«1.Скорость первой точки в любой точке r 1 ГФ в <\ р т ’ й-у \ Т = Скорость 2-й точки была найдена выше. Равняйте эти 2 значения коэффициента скорости, чтобы определить точку T, где скорость обеих точек одинакова. т = — а Я… После простого преобразования, это, наконец, выглядит так: т. Для овладения навыками решения задач по определению скорости и ускорения точек И. В. Мещерский из»сборника задач теоретической механики» с 1950 года рекомендует решать следующие задачи:322、323、32
5、330、341、346 、352、353、363、367、370、371、372、373、374。 л, д-д, дБ, да Где y = = = — = — есть, и поэтому нормальное ускорение равно 2. = — =ХІ | Ф(21 *) В этом разделе рассматриваются вопросы, связанные с определением радиуса кривизны орбиты с использованием скорости точки, определения ускорения и известного уравнения движения для точки. Определение скорости и ускорения точки по заданному уравнению движения сводится к производной уравнения движения и всегда может быть выполнено как в аналитических, так и в графических задачах точки motion. At в то же время, другие функции данны
х Движение точки: любое мгновенное положение, скорость и ускорение в качестве максимального и минимального значений. При решении задачи определения скорости и ускорения полезно следовать следующей последовательности: 1) Выбрать систему координат. ri 2) Создайте уравнение движения Точки в выбранной системе координат. 3) используя уравне
ние движения точек, определите проекцию скорости и величину и направление скорости по координатным осям. 4) знает проекцию скорости, определяет проекцию ускорения на координатные оси и ускорение по величине и направлению. Если траектория точки задана в соответствии с условиями задачи, то рекомендуется применить естественную форму к уравнению движения и искать ускорение точки через проекцию на ось естественного трехгранного тела. В этом разделе мы также решаем задачу определения уравнения движения точки и ее траектории, если нам известно ускорение. При решении задач по определению уравнен
ия движения точки и ее орбиты рекомендуется следующая последовательность действий: 1) Выберите систему координат. 2) проекции ускорения на эти оси. 3) интегрируйте полученные зависимости и найдите прогноз скорости. 4) в найденном выражении определите любую константу интегрирования, используя известные значения скорости предсказания в заданный момент времени. 5) интегрируем полученные зависимости прогноза скорости и получаем уравнение движения точки.
Смотрите также:
Предмет теоретическая механика
| Центр тяжести | Вращение твердого тела вокруг неподвижной оси |
| Траектория и уравнения движения точки | Преобразование простейших движ ений |
