Оглавление:











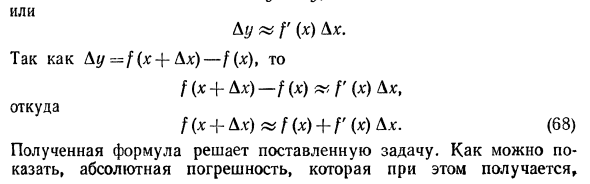





Дифференциал функции
- Функция отличается. Дифференциация функции и ее геометрическое значение Рассмотрим функцию r = x3. Найти приращение Av%, соответствующее приращению аргумента Ax в точке x0O. y = (x-yes 🙂 5 — x3 = 3.v2 yes: + bx (Axf + (yes 🙂 3 = 3x2Dlg + (For: + yes 🙂 (yes :)) 4. Как видите, приращение функции можно рассматривать как сумму двух слагаемых: первый bxrAx является линейным по отношению к Да: (точнее пропорционально Да :), второй — (3x-f-Да: ) (Да 🙂 2, нелинейный по отношению к Да: Дя— В случае * • () оба термина бесконечны. Другими словами, он стремится к нулю. Но в то же время второй член стремится к нулю быстрее, чем первый член.
lim Urn (3, D * + (D *)>) = 0 D * -OX BX OX _ q В результате для небольшого Ax приращение функции можно считать практически равным ее линейной части: Du x bx * Ax. В связи с этим линейная часть приращения называется основной частью функции приращения. В следующей таблице значение приращения функции Ду-3Да указано для функции y = x3 в точке x = 1. -f 3 (Дх) а (Да-) 5, его основная линейная часть ЗДа и нелинейная часть 3 (Dx) 4 + (Dx) 1 для различных значений Ax. d * Линейная часть ЗДхНелинейная часть 3 (Д *) а + (J) » 0,1 0,331 0,3 0,031 0,01 0,030301 0,03 0,000301 0,001 0,003003001 0,003 0,000003001 Во многих случаях точное значение s и, следовательно, абсолютная ошибка q неизвестны. Поэтому вводится понятие границ абсолютной ошибки.
Другими словами, ограничение на отношение второго члена к первому члену равно нулю. Людмила Фирмаль
Определение Границей абсолютной погрешности приближенного значения u0 является любое положительное число D0, которое больше или равно абсолютной ошибке D „. s0 | = Дп <Дц. (67) Из неравенства (67) точное значение величины находится между u0-AP и w0 + D0. u0-Dt <u <u0-f Dy. Если абсолютная погрешность, связанная с нахождением определенной величины, равна Di, они говорят, что значение u было найдено с точностью Di. Понятно, что чем меньше Dy, тем точнее можно найти величину u.
Однако, поскольку вы знаете предел погрешности, вы еще не можете определить качество аппроксимации. Так, например, измерение расстояния от Москвы до Ленинграда с точностью до 1 км имеет гораздо большую абсолютную погрешность, чем измерение роста человека с точностью до 10 см. Однако ясно, что качество измерения в первом случае выше, чем во втором. Понятие относительной погрешности вводится для определения качества аппроксимации. Определение Относительная погрешность — это отношение абсолютной погрешности Dv к модулю измеренного значения приблизительного значения u0.
| Производная | Функции, заданные параметрически, и их дифференцирование |
| Производные высших порядков | Векторная функция скалярного аргумента |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Когда относительная ошибка представлена 6a, Определение Граница относительной погрешности ba — это отношение абсолютной погрешности dy к абсолютной величине метода u0 измеряемой величины. L и 6 часто выражаются в процентах. Возвращаясь к рассмотренному примеру, найдите границу между расстоянием L от Москвы до Ленинграда и относительной погрешностью измерения длины / роста человека. Около L «650 км и /« 170 см. ^ 0,0015 или 0,15%. Во втором случае 10 = \ 70 см, Д, 10 ^.
Следовательно, fy = ^ «0,0588 или 5,88%. Далее мы рассмотрим применение дифференцирования к приближенным вычислениям значений функций. Каково значение функции y = f (x) и ее производной в точке x? Вот как найти значение функции / (лr — :)) 🙂 Вблизи точки x — \ — Ax. Для этого воспользуемся приближенным уравнением (59). Ду ты, или Dg / ^ / ‘(a 🙂 D *. \ y-f (x — \ — Dx) -f (x) f (x + bx) -f (x) tf MΛ *. Откуда f (x + \ x) tf (x) + f (x) bx. (68) Полученное выражение решает проблему. Получена абсолютная ошибка, как показаноНе превышать Где M — максимальное значение \ T (x) \ для сегмента [x, x + Ax].
Измерение Первый случай гораздо точнее, чем второй. II. Людмила Фирмаль
Пример 1. Найти приближение cos 61 °, используя уравнение (68). Решения. Рассмотрим cos61 ° как конкретное значение функции y = f (x) = cos *. Получить начальное значение аргумента x = 60 ° или радианы x = — | — (cos * легко вычисляется Нет таблицы). О новом (увеличенном) значении аргумента a: -g да: = 610 или радианы = Тогда приращение аргумента 61 я 180 Подстановка числовых значений x и Ax дает здесь cos 61 ° или cos 60 ° при 60 °. 0.01745 = i-_.il! -0,01745 «0,4849. Чтобы оценить ошибку, вторая производная f (x) = (cos x) «- cos x. Для всех n: между 60 ° и 61 ° | f» (x) | = = | -cosx | Если <l, абсолютная ошибка в уравнении (69) не превышает м Аху <~ (0,01745) 2 «0,0003.
Следовательно, ошибка не превышает 0,0003. Пример 2. Примерное увеличение объема цилиндра на высоте Н = 40 см, радиусе основания R = 30 см и увеличении радиуса основания на 0,5 см. Решения. Объем V цилиндра при постоянной высоте H и переменном базовом радиусе R является функцией R: V = nHR2.
При расчете приращения объема переменного тока замените это приращение на разницу dV = 2nHR-AR. AV и 2nHR-AR. Если D # = 0,5 см, R = 40 см, R = 30 см, ДВ «2л • 40 • 30 • 0,5 = 1200я» 3770 (см9). Используя уравнение (69), читатель легко может быть уверен, что абсолютная погрешность, ограниченная в этом случае, составляет Sv = 31,4 ежа 3. Дифференцирование высшего порядка Рассмотрим функцию y = f (x) и предположим, что ее аргумент x является независимой переменной. Производная этой функции dy-f ‘(x) dx зависит от двух переменных x и dx = Ax, dx не зависит от x (приращение конкретной точки x можно выбрать независимо от этой точки ).
Если вы рассматриваете dy = f ‘(x) dx только как функцию от x (то есть учитываете константу dx), вы можете найти производную этой функции. Производная от производной данной функции y_f (x) называется ее второй производной (или второй производной) и представлена d2y и d2f (x). «De two igrek» или «de two ef from x»). Так по определению d2y = d (dy). Найти выражение второй производной функции y-f (x) i d2y —d (dy) = d [/ ‘(x) dx] = [/’ (x) dx] ‘dx = fn (x) dx-dx ^ f (*) (dx) \ После дифференциации dx считался постоянным. Далее мы опускаем скобки мощности dx.
Тогда уравнение d2y имеет вид: d2y = f «(x) dx2. (70) Производные, такие как третий порядок и четвертый порядок, определяются и обнаруживаются аналогичным образом. В общем, n-я производная (или n-я производная) функции y-j (x) является производной от (n-1) -ой производной. R-ая производная функции y = f (x) обозначена dny или dnf (x). Так по определению dny = d (d «-1 y). Производная функции dy также называется первой производной. Установить действительность выражения легко dny = fin) (x) dxn (71)
Для функции y = f (x), аргумент которой является независимой переменной. Из уравнения (71) rw = 0-. (72) Особенно, когда η = 1, 2, 3 RW-4.rw-3.rw-г Другими словами, n-я производная данной функции (если аргумент является независимой переменной) Он рассматривается как отношение i-й производной к n-му порядку независимой переменной производной. В разделе 4 мы обнаружили, что первая производная форма dtj-f ′ (x) dx обладает инвариантными свойствами.
Однако дифференциальные формы высшего порядка (n> 1) dny = f (/,) (x) dxn не имеют инвариантных свойств. Это означает, что если аргумент не является независимой переменной, то уравнение (71) (когда η> 1), как правило, неверно. Уравнение (72) в этом случае (когда η> 1), как правило, неверно. Следовательно, производная fln) (x) (n> 1), когда x не является независимой переменной, не может рассматриваться как отношение d «y к dxn. ДНУ Тем не менее я согласен сохранить обозначение fn (x) — jx% i.
Понять как новое символическое представление n-й производной, а не как производное отношение. Из этой таблицы мы можем ясно видеть, как быстро нелинейная часть DN уменьшается при уменьшении Ax по сравнению с основной линейной частью DN. Подобные свойства предоставляются для многих функций. Предположим, что приращение Au функции f (x) в точке x можно выразить как Au = L • Dx-ba (Dx), (57) Где Yes — приращение аргумента, вызвавшее приращение функции Au \ A является константой (т. Е. Независимым значением Ax). a (Ax) — бесконечно малая функция малого порядка.
Чем ах. Lim = Корректировка функции y = f (x) в точке определения x Когда А выражается уравнением (57), основная часть приращения функции A Ax, пропорциональная приращению аргумента, называется производной этой функции , Производная функции y = f (x) представлена символом dy (читается «de igrek») или df (x) (читается «de eff from x»). Так по определению DY = L Ах. (58) Таким образом, если функция y = f (x) имеет производную в точке x, приращение в этой точке является суммой двух слагаемых: производная / / = АхAx и нелинейная часть a (Ax порядка Ax меньше, чем Ax of Ax ) -0. Таким образом, игнорирование нелинейного терма малого Ax дает следующее приближенное уравнение: И «L Ах, или И умереть. (59)
Теперь рассмотрим теорему, которая устанавливает связь между существованием производной и существованием производной. Если функция теоремы y = f (x) имеет производную в точке x, то в этой точке есть производная. Доказательство. В зависимости от условия функция // = f (x) имеет производную, поэтому ее приращение A y может быть выражено уравнением (57). A * / = LAX- | -a (Ax) и lim a (Лдг) _q (57) Dh-0 Если вы пройдете предел как Ax-> 0: Лит Лим Лим * * «(А *)„ Я + Иш = Ah- * 0 D * 0 LH Dx 0 Ho lim-r- = f ‘(*), поэтому существует производная f (x) о И равно А В результате формула разности имеет следующий вид: dy = r (x) x. (60)
Таким образом, существование производной означает существование производной, то есть дифференцируемость функции. Наоборот, дифференцируемость функции указывает на существование производной. Другими словами, справедлива следующая теорема. • Теорема: если функция y = f (x) имеет производную в точке x, в этой точке есть производная. Доказательство. Предположим, что функция y = f (x) имеет в точке x Производная f ‘(x) = урна Dh-0 Кодированный х является функцией приращения Да.
Все функции с ограничениями равны сумме этого ограничения и нескольким бесконечно малым функциям (см. Гл. V, § 1, раздел 6). так (61) Где B (да) — это бесконечно малая функция от yes, то есть Lira P (yes) = 0. dh- О Умножьте равенство с обеих сторон (61), умножив Да Dy = f ‘(a) ДА + ДА p (ДА). (6P Рис. 137 Таким образом, приращение функции Du является суммой двух слагаемых: / ‘(a) Да и Dx-P (Да). Кроме того, первое слагаемое пропорционально Да, а второе слагаемое Да — 0 равно Бесконечно маленький выше чем да Hm lim P (да) = 0 Dx- * 0 Dh-0 Таким образом, согласно определению, приведенному выше, функция y = f (a) имеет производную, равную yes, в точке a, f ‘(a).
Следовательно, концепция дифференцирования функций и существования дифференцируемости эквивалентны. Найти геометрическое значение дифференциации. Для этого нарисуйте касательную к графику функции y = -f (a) в точке M (a; y) и укажите угол с осью Ox как os (рис. 137). Рассмотрим ординату этой касательной точки -} — да. Отрезок NP, равный разности между этой ординатой и касательной ординатой точки a, называется тангенциальным приращением ординаты. Указывает, что этот сегмент равен производной д.
Из правого треугольника MNP: NP = tg a * MNt или NP = tga-bx. Но в соответствии с геометрическим значением производной tan a = f ‘(*). так NP = f ‘(x) \ x = dy. Я нашел геометрическое значение дифференциации. Производная функции y = f (x) в точке x равна тангенциальному приращению ординаты.Производная как отношение производной Рассмотрим функцию y = x. Согласно уравнению (60), его производная равна dy = dx = (x) ‘Ax = 1 • Al: -Ax Согласитесь называть производную независимой переменной производной функции, равной x.
То есть предположим, что производная независимой переменной равна ее приращению. дх = ах (62) Уравнение дифференцирования функций (60) записывается в следующем виде: dy = f (x) dx. (63) Разделив обе части этого уравнения на dx, получаем: fx = f ‘(*) ■ (64) Таким образом, производная функция равна отношению этой производной к производной независимой переменной. Во многих случаях это отношение просто считается символом, Показывает производную от у по х. 3.
Различия в сумме, продукте и конкретной функции Пусть u = * u (x) и v = v (x) — дифференцируемые функции от x. Далее выполняется следующее уравнение. d (u + v) = du + dv, (65) d (uv) -и du -f v du, (65 ‘) d (il) __v du — и dv (при условии, что v f 0) # (65 «) Предоставьте читателю вывод уравнений (65) и (65 «) и ограничьте его выводом уравнения (65 ‘). d (uv) = (uv) ‘dx = (u’v-b uv’) dx = vu’dx -f- uv’dx = vdu — \ — udv, UDX — быть Du и VDX — быть Du. Пример. Найти производную функции = решение. Из уравнения (65 ‘) dy = xh (ex) + exd (x2) x \ ex) ‘dx + e * (x2)’ dx = xe * (x + 2) dx. 4. Комплексная функция дифференциации.
Дифференциальная форма инвариантности В разделе 2 мы обнаружили, что когда x является независимой переменной, производная функции y = f (x) имеет вид dy = f ′ (x) dx. (66) Указывает, что эта форма также сохраняется, когда x является функцией, а не независимой переменной. На самом деле * / = f (*) и x = φ (0, т. Е. У — комплексная функция от /. — / В случае [φ (0). dy = y ‘(dt. Правила дифференцирования сложных функций дают y’t — y’x-x’t. dy = y’x-x’t dt «tjxdx- / ‘(l) dx, с того времени х) дт-дх. Докажите следующую теорему. Производная комплексной функции y = / (x) с теоремой x = (p (/) имеет ту же форму, что и dtj-j ‘(x) dxy, как если бы аргумент x был независимой переменной.
Дифференциальная характеристика комплексной функции, выраженная этой теоремой, называется дифференциальной инвариантностью формы. Из уравнения (66), производное уравнение Если аргумент * не является независимой переменной, он сохраняет свой формат. 5. Применение дифференцирования к приблизительным значениям расчет 1. При приближенном расчете мы сталкиваемся с понятиями абсолютной ошибки и относительной ошибки. Определение Абсолютная ошибка приближенной величины u0 — это абсолютная величина разницы между точным значением этой величины и ее приблизительной величиной u0. Абсолютная ошибка из-за символа A „ = I «-» o |.
