Оглавление:



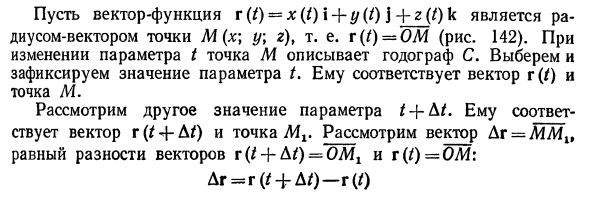



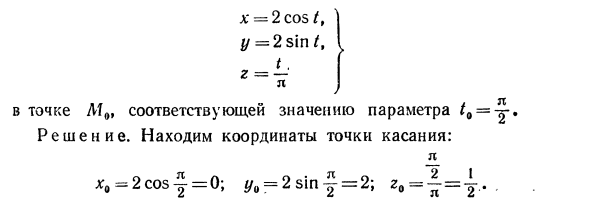





Векторная функция скалярного аргумента
- Векторная функция скалярного аргумента 7. Параметрическое уравнение пространственной кривой Кривые в пространстве и плоскости могут быть определены параметрически. Рассмотрим три функции переменной t. y = y (i),} (60) , 2 = 2 (/) J Найти проекцию вектора r ^ / ,,): (0 = (2 cos t) ‘ -2sin | = -2; = 2cos | = 0; y ‘(t „) = (2 грех I) L! Z l _y — 2_g_2 -2 0-1 Найти уравнение касательной, используя уравнения (85) и (86). L И нормальный самолёт или 4 лк — 22 + 1 = 0. 4.
Давайте проясним механический смысл первой производной вектор-функции. Масса движется вдоль кривой, описываемой концом вектор-функции r = r (/) (т.е. годографом вектора r), параметр t означает время пробега. Скорость движения материальной точки в момент времени t, v = v (t), представляет собой вектор, направленный вдоль тангенса траектории. Если это в направлении движения и абсолютные значения lim равны (как проход) д / о с Начать в момент времени t и пройти через точку с интервалом времени At. Производная r ‘(/) от радиус-вектора r (/) в точке движения указывает, что скорость движения v = v (/) в этой точке. В §3 вектор r ‘(t) = lim- Касательный годографа вектора r. Вектор гм,
Механический смысл первой и второй производных скалярных аргументных векторных функций Людмила Фирмаль
Фактически вектор r ‘(/) направлен в направлении движения точки (см. Рис. 142). Таким образом, вектор r ‘(*) имеет то же направление, что и вектор скорости v. Указывает, что модули этих векторов одинаковы. Фактически, как длина дуги (то есть путь, пройденный до точки, где At> 0) | Ar | I Ag As 1 m == | as D / | Где | Ar | — длина кода MMlt, а As — длина соответствующей дуги MAiv.
Предел отношения между длиной дуги и длиной строки, которая тянет строку, равен 1: lim 14 ^ = 1. Где lim = 1 и в результате О -с A / Об As- * Ds А с конкретно = lim L ^ J • lim lim в качестве Потому что Iga- = | v |, a, о Ag О? A / 0 ‘^ Ar = | r ‘(0 |, TO Рон, Рим Д / -о в g- (O I = IV (01. Таким образом, векторы r ‘(/) и v (t) имеют одинаковый модуль в одном и том же направлении. так r ‘(0 = v (/). Следовательно, производная r ‘(/) вектор-функции равна скорости движения массы \ (t) в конкретный момент времени t.
| Дифференциал функции | Некоторые теоремы о дифференцируемых функциях |
| Функции, заданные параметрически, и их дифференцирование | Неопределенный интеграл и его свойства |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Это механический смысл первой производной скалярной аргумент-векторной функции. Производная r ‘(/) вектор-функции r (/) является вектор-функцией скалярного аргумента tt и, как правило, может быть дифференцирована. Производная от r ‘(/) по скалярному аргументу t называется второй производной вектор-функции r (/). На это указывает gr (t) или ^ jr. так \ s было найдено, что r ‘(/) = v (/). так DV (T) (88) дт «40 Вектор a (t), равный производной по времени скорости v (/) по времени, называется ускорением. Итак, вторая производная (87) Рис. 143
g «(0 вектор-функция равна ускорению движения точки массы в данный момент времени t. Пример. Найти скорость и ускорение массы M, которая движется по окружности + = с постоянной угловой скоростью o) (рис. 143). Решения. Угол вектора радиуса точки М обозначается как <р Для оси Ox условие = или φ = ω /.
Это механический смысл второй производной скалярной функции-аргумента вектора. Людмила Фирмаль
Где т это время Движение. Это позволяет x и y координаты точки M быть выражены следующим образом:Функция времени /: х = /? coscp = tfcosco /; y = R sin cp = R sinω /. Следовательно, радиус-вектор точки М r = x \ -} — y) = I cosω / • i + R sinсо / • j. Здесь вы можете легко найти скорость v (/) точки М. v = r ′ (/) = (I cosω /) ′ i + (R sinω /) ′ j = −R sinω / • i + Ra cosω / • j. Найдите модуль скорости: v | = V \ -Rio sinω /) 2 + (tfco cosω /) 2 = ω /?
Легко непосредственно подтвердить, что скалярное произведение векторов v и r равно нулю, так что векторы v и r перпендикулярны друг другу. Таким образом, вектор v касается круга, вокруг которого движется точка M (см. Рис. 143). Ускорение найдено (/): a (/) = r «(/) = -tfco3 cosо) / • i-Ra * sinω / • j. #Cosco / -i- | — /? Поскольку Sinco / -j = r (/), a (/) = -co2r (/). В результате векторы r и a находятся в противоположных направлениях. Поэтому ускорение точки массы, которая движется по окружности с постоянной угловой скоростью в каждый момент, направлено к центру этого круга (см. Рис. 143).
Имеют ту же область определения. Каждое значение t в этой области соответствует определенному значению x, y и r и, как следствие, соответствует определенной точке M (x; y \ r) в пространстве. При изменении t точка M представляет собой конкретную кривую C в пространстве. Я согласен, что эта кривая параметрически определяется уравнением (80). Переменная t называется параметром. Ваше IV (§ 2, пункт 3) параметрическое уравнение прямой в пространстве уже учтено: x = mt + xlt y — nt — \ — yx> z = pt + zv Вот еще один пример. Рассмотрим параметрически определенные кривые, используя уравнения х = стоимость, \ y = as \ nt, [(81) z = bt. ) Эта кривая называется спиралью (рис. 140).
Для любого значения параметра t xi + if = a2 (cos21 + sin21) = a \ Это означает, что спираль находится на цилиндре. xi + y% = a *. Когда точка M движется вдоль спирали, проекция N на плоскость Oxy движется по окружности с радиусом a, а t представляет собой полярный угол точки N. Если параметр t увеличивается на 2n, точка N представляет полный круг, а строка z точки M изменяется на h = 2nb. Это значение называется спиральным шагом. 2. Векторная функция скалярного аргумента и ее производная Дайте кривую параметрически пространственно по уравнению (80)
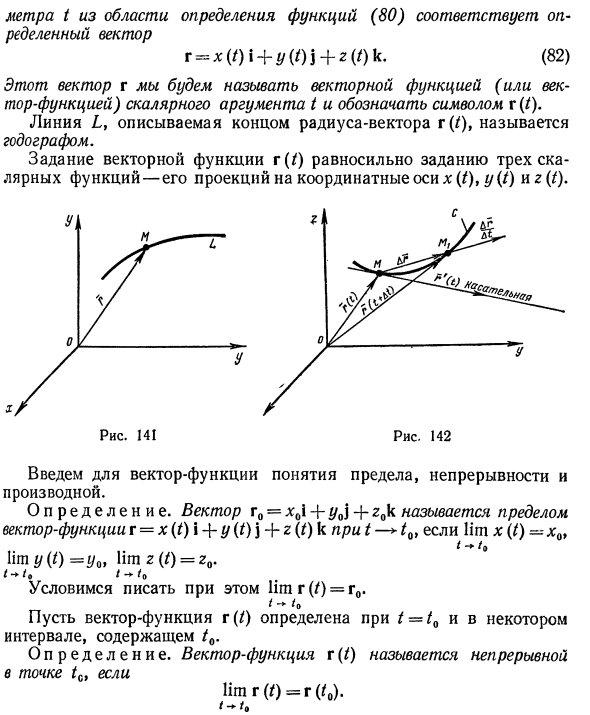
x = * x (t) 9] Y = Y (*). [ 2 = 2 (0-J Как мы видели до сих пор, каждое значение параметра, принадлежащее области определения функций x (t), y (t) и z (t), имеет определенную точку M (x \ y \ z). Однако каждая точка в M соответствует радиус-вектору r = rOM, ее начальная точка совпадает с началом координат, а ее конечная точка совпадает с точкой M (рис. 141). Проекция этого вектора на координатную ось определяется уравнением (80), поскольку оно совпадает с координатами точки М. Поэтому пара- Измеритель t из области определения функции (80) соответствует определенному вектору r = x (t) \ + y (t) i + z (t) k (82) Этот вектор r называется вектор-функцией (или вектор-функцией) скалярного аргумента t и обозначается символом r (t). Линия L, описанная в конце радиус-вектора r (/), называется годографом. Определение векторной функции r (/) эквивалентно определению трех скалярных функций, которые проецируются на оси координат x (t), y (t) и z (t).
Вводит понятие ограничений векторной функции, непрерывности и производных. Вектор определения r0 = x0 \ + y0] + z0 k называется ограничением Векторная функция r = x (t) \ + y (t) \ + zlt) k при t-> tQt, если lim n: (t) = -xQ> t- + t0 лира y (0 = y09 lim z (t) = zQ. Я согласен написать limr (/) = r0. К / — Векторная функция r (0 определена для t = tQ и определена на определенном интервале, включая / 0. Функция определения вектора r (/) называется непрерывной в точке tc. lim r (0 = r (d.
Функция вектора r (t) = x (t) i + y (/) j-jz (t) k является радиус-вектором точки M (x \ y \ r), то есть v (t) -OM (фиг. 142) ). Когда параметр t изменяется, точка M представляет годограф C. Выберите значение параметра t и исправьте его. Вектор r (/) и точка M соответствуют ему. Рассмотрим другое значение параметра / + D /. Вектор r (/ — {- /) и точка Mg ему соответствуют. Вектор Aj = MMlt считается равным разности между вектором r (/ + At) = OM1 и r (t) = OM. Дг = г (/ + А /) — г (/)
Вызывается приращение вектор-функции r (t) в точке t. Пожалуйста, рассмотрите отношения ^. Коллинеарный вектор Вектор Dg. Потому что скалярный коэффициент отличается Определение Производная вектор-функции r (t) по скалярному аргументу t является новым вектором, равным пределу отношения приращения вектор-функции Dt и соответствующего приращения аргумента Dt. Однако At стремится к нулю.
Функция вектора r (производная от 0 равна г (0 или Так по определению (T) = лим. (83) От -0 до Выразите производную вектор-функции r ‘(t) по проекции на оси координат. с того времени r (t) = x (t) x + y (t)] + z (t) kr (t + At) = x (t — {- At) i + y (t + At) \ -tz (t + at) k, тогда Dt = T (tt dt) -r (0 = [x (t + At) —x (/)]! + + [Y (t + At) -y (01} + [z (t + At) -z (/)] К Таким образом, Ar_s (/ -f AQ- * (/) y (t + M) -ij (t). Z (/ — {- A /) — r (/). A / S A / ‘J D / K- так r ‘(<) = lim £ = i lim + j, im »m> + д / -о д / -0 д / о д / — * о + k lim (0 | + (/) j + r ‘<<) k. Д т Вот так T ‘(0 = X? (T) \ — {- y’ (0J + r ‘(0 к. (84)
Уравнения касательной и нормальной плоскости К пространственной кривой Найти направление вектора r ‘(/). Вектор ^, коллинеарен Вектор Дг вдоль секущей линии MMt (рис. 142). В случае A / -►O точка Mt приближается к точке M бесконечно, а секущий MM1 приближается к касательной L кривой C в точке M бесконечно. Таким образом, вектор r ‘(/) направлен вдоль касательной годографа радиус-вектора OM = r (f).
Найти уравнение касательной к пространственной кривой, определяемой параметрически уравнением (80) в некоторой точке Y0 * 2o). Соответствует значению параметра t = t0. Эта касательная является прямой, проходящей через точку M0. Следовательно, уравнение можно записать в следующем виде (см. Главу 4, § 2, с.4). * — * 0 y— Ya % Zp mp 1 Где m, n и p — проекции вектора направления линии. вектор r ‘(t0) = x’ (t0) \ + y ‘(‘ o) i-u’Co) k Ориентирована вдоль касательной кривой в точке M0, и ее проекция может быть получена в качестве направляющей векторной проекции. m = x (t0), n = y (t0), p = z (t0). Далее, касательное объективное уравнение принимает вид: A «-U o _ U-Y0 __ Z-Z0 x ‘Wv’ilo) -g’ «o) l K ‘
Вы можете видеть, что плоскость, перпендикулярная кривой определения пространства, перпендикулярна касательной и проходит через контакт. M0 (a0; y0 \ z0) — контакт. Выведите уравнение для нормальной плоскости через эту точку. Форма плоского уравнения через заданную точку M0 (x0 \ y0 \ r0) имеет вид A (x-x0) -B (y-y0) + C (r-r0) = 0, Где A, B и C — векторы N {/ 1; B \ C) — перпендикулярно этой плоскости (см. Главу IV, § 1, с.2). Однако из определения нормальной плоскости вектор Γ ′ (> o) {* ′ Co); y ′ (t®); 2′Co)} относительно вектора N. Следовательно, A = * (t.), B = if (/.), C = z ′ (t0). В этом случае искомое уравнение для нормальной плоскости записывается в виде (/.)■•(■-.)+У ‘(/.)■•(У-Уо)+г'(/о)•(г-г)=0. (86) Пример. Найти касательные и спиральные нормальные уравнения
