Оглавление:







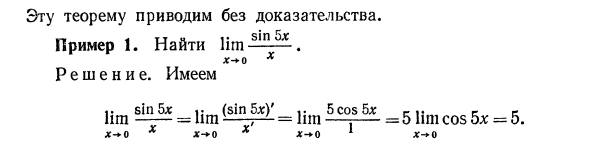

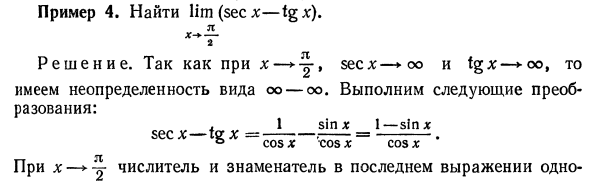



Некоторые теоремы о дифференцируемых функциях
- Некоторые теоремы для дифференциальных функций. /. Теорема Ферма * Предположим, что функция / (*), определенная интервалом теоремы (i, b), принимает максимальное или минимальное значение в некоторой точке этого интервала. В этом случае, если в точке c есть производная этой функции, она равна нулю. Доказательство. Для ясности, пусть / (c) = M — максимальное значение функции в интервале (a, b). f ‘(c) = 0 По определению производных / ‘(C) = Hm / f (c + Dx) и f (c + Dx) -f (c) <0
Другими словами, перейдите ко второму производному отношению. Пример 2. Найти НшУ ~ с * 4х. х — * — о х Решения. Здесь числитель и знаменатель имеют тенденцию быть равными нулю одновременно. Если вы применяете правило больницы дважды, 1-cos 4x, 4 sin 4dg ..16 cos 4x 0 «. L 0 lim —tt = lim — = — = lim-s— = 8hmcos4x = 8 X-0 x x- + огхX- * 0 1 X- + 0 Е Пример 3.
Если коэффициент производной снова неопределенный 0 оо Если отделимость имеет вид или, доказанная теорема может быть применена повторно. Людмила Фирмаль
Найти лим. \ х- + + а> е Решения. Здесь числитель и знаменатель являются бесконечно большими функциями, такими как x — * — 4-oo. Если вы применяете правило больницы дважды, lim lim lim ~ = 0. X- * + SS X- + <*> СX-b + ОО Точно так же в общем lim «o» «+ + … +», = 0> х- + со е То есть, любой полином степени возрастает медленнее, чем экспоненциальная функция. В дополнение к неопределенности формы -jj- Существуют следующие типы неопределенностей. Неопределенность формы оо-оо. Это раскрытие неопределенности означает нахождение предела lim [/ (x) -Φ (x)] *. X- + C 1 (x) и φ (x) — бесконечно большие функции одного и того же знака, а именно Jim f (x) = oo и limφ (x) = oo. X- + C x- * s В этом случае путем преобразования выражения / () — φ () Ах ах Видовая неопределенность или
Пример 4. Найти lim (secx — tg x). Я X — * — 2 Решения. x —►-, сек x-► ° и tgx—> 00, Существует неопределенность формы oo-oo. Выполните следующее преобразование: , 1 грех * я — грех * sec l: -Tax ——.- = -. & Cos x cos x cos x Для х последний числитель и знаменатель равен 1 Есть тенденция временно стать нулем. Таким образом, вы получаете неопределенность формы. Используя правила больницы, l ^ slnx = „-COS * = 0 l cos x i sin * 2 2 Следовательно, lim (secx — tg x) L х-2 Неопределенность формы O-OO.
| Функции, заданные параметрически, и их дифференцирование | Неопределенный интеграл и его свойства |
| Векторная функция скалярного аргумента | Основные методы интегрирования |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Такое раскрытие неопределенности означает нахождение предельного лимита [/ (x) 0, поэтому Существует неопределенность формы oo-O. Преобразуйте это выражение в: lim tg 2x [tg x — ctgx] = lim tg * ~ 5 *. X- * 3l / 4 X- * Jtf A ClS ** RP 0 Поскольку мы уже получили неопределенность вида -q-, мы можем применить правило правила. 1 1 lim tg * ~ ctgx = lim cos2jc 9si «2 ‘= -2. X.- I / 4 F / 4 г sin2 2x Итак, наконец: lim tg2x {tgA: —ctgx] = -2. X- * ZT / 4 Неопределенность формы 100. При таком раскрытии неопределенности предел lim [/ (x)] φ (* \ if lirn / (x) = l, X- * C X- + C lim f (l 🙂 = oo. X- + C
Неопределенность пены 0 °. Неопределенность формы oo °. Раскрытие такой неопределенности означает определение предела lim [f (x)] phi), если lirn / (x) = oo и lim ph (x) = 0. X- + C Неопределенности вида 1 °, 0 ° и ° ° обычно уменьшаются в случае неопределенностей формы q- или — на логарифм выражения [/ (x)] phi).
Из-за этого раскрытия неопределенности, предел lim [/ (*)] phi)> if if [Whip [(x) = 0 X- * C X- + C И ПТФ (х) = 0. х- * с Людмила Фирмаль
Пример с. Найти lim (1 + l: 2) *. X- * + SS Решения. В этом случае (1 -fx2) —oo, i►O и Тип неопределенности oo °. у = (1 + ху, х. логарифм, Поскольку x-> H-oo, числитель и знаменатель имеют тенденцию быть бесконечными, что приводит к следующей форме неопределенности: Применить правило столицы. 2 раза lim iny = lim! Λ11 ± £! ) = Iim я + fl ^ o. X- * + SS + 00 X X- «+ 00 Поскольку функция 1nn непрерывна, lim (In y) = In (lim y) \ X — ++ OD X ~ * + CO Следовательно, In (lim y) = 0 и lim y = 1. Следовательно, lim (1 −1 — x2) 1 / * = 1. ДГ- * + сЖ — »+ СОХ- * + <Х> Замечания. Согласно закону Риттала, если существует ограничение на отношение производных этих функций, то существует ограничение на отношение самих функций.
Если нет предела отношения производной, это не означает, что нет ограничения на отношение самой функции. Например, рассмотрим две бесконечно большие функции x-> + oo: f (x) = x + sinx и φ (x) = x. Предел отношения как x — »-} — oo существует. n_ / £) ит £ 5! n £ wit fl + shL * — + oo H> <*) x-> + oo * x- * + co V * J Однако соотношение данных производных функций ограничено. φ ‘() ()’ -1 + cosx не существует. cosx не имеет ограничений по x -> — oo.
Следовательно, если Ax> 0, то I —— <0, G (секунд) — Рис. 144 Планировать Следовательно, производная / ‘(с) не является ни положительной, ни отрицательной. Следовательно, Γ (c) = 0. Геометрически теорему Ферма можно объяснить следующим образом. Поскольку производная равна тангенсу угла a, образованного касательной к графику функции с горизонтальной осью, уравнение / ‘(c) = tga = 0 является абсциссой, где функция имеет максимальное или минимальное значение Указывает, что касательная функции параллельна в точке с осью c Ox (рисунок 144). если xa D * <0, и R (s) = lim Ах ах
Теорема Роля ** Теорема »Если функция f (x) непрерывна на отрезке [a, b], дифференцируема во всех ее внутренних точках и исчезает в конце отрезка: f (a) = f (b) = 0, Его производная f (x) исчезает хотя бы в одной внутренней точке этого отрезка. Доказательство. Поскольку функция непрерывна в сегменте, максимальное значение M и минимальное значение m достигаются в этом сегменте (глава V, § 2, пункт 3). Если == — m, функция является постоянной в сегменте \ a, 6], поэтому ее производная / ‘(*) — 0 находится в любой точке сегмента. Где Mft> является одним из этих чисел, например, MF 0.
Поэтому, если максимальное значение M достигается в точке c: если f (c) = M, точка c должна быть внутренней точкой отрезка [a, 6]. Принадлежит интервалу (a, b) (/ (a) = / (6) = 0 от конца отрезка). Следовательно, f ‘(c) = 0 согласно теореме Ферма. Геометрически теорему о роли можно объяснить следующим образом: график функции, непрерывной в отрезках [a, b] и дифференцируемой внутри нее, представляет собой Ox в двух точках x = a и x-bt При пересечении оси существует, по крайней мере, одна точка c, a <c между этими точками <6, и касательная графика параллельна горизонтальной оси (см. Рисунок 144).
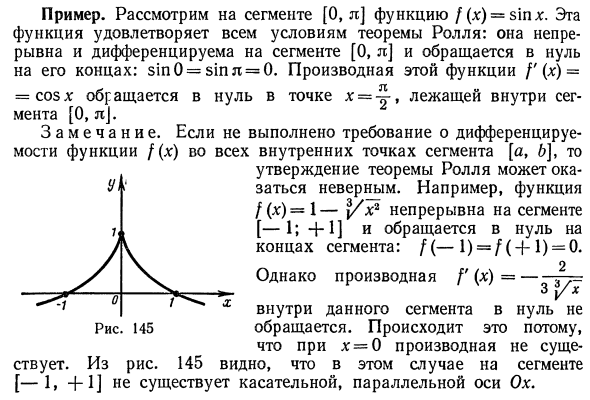
Пример. Рассмотрим функцию f (x) = s \ nx на отрезке [0, x]. Эта функция удовлетворяет всем условиям теоремы о роли. Он непрерывен и дифференцируем в сегменте [0, l] и исчезает в его конце: sinO = sinñ = 0. Производная этой функции / ‘() = = cosx — это точка x = отрезок [0, jiJ. Замечания. Если требование дифференцируемости функции f (x) не выполняется во всех внутренних точках отрезка [a, 6] Описание теоремы о роли может быть неверным. Например, функция / () = 1—1 / x2 непрерывна в сегменте [—1;. +1] и исчезают в конце сегмента: / (-1) = / (-} — 1) = 0. 2 Где производная / ‘(х) = — 3 Дж / х Нули в этом сегменте не показаны. 145 адресов. Это Если x = 0, производной нет. 145 В этом случае вы можете видеть, что отрезок [-1, -f 1] не имеет касательной, параллельной оси Ox.
Теорема Лагранжа . Если функция теоремы f (x) непрерывна на отрезке [a, b] и дифференцируема во всех ее внутренних точках, в этом отрезке есть хотя бы одна точка c, для которой выполняется уравнение. IMzM = f ‘(c). (89) Доказательство. На рисунке 146 показан график функции y = f (x). Напишите уравнение для кода AB. Это использует уравнение прямой через две точки A [a \ J (a)] и B [b \ f (b)]. y-f (a) x — a f (b) -f (a) b-a ‘ Отсюда определяется ордината кода Теперь рассмотрим вспомогательную функцию F (x), равную разности хорд, соответствующей тому же значению x, что и ордината графа функции. F (x) = f (x) — [/ (a) + nb) bZaa) ( — «)] •
Нетрудно убедиться, что эта функция удовлетворяет всем условиям теоремы о роли. На самом деле функции f (x) и x — a непрерывны, поэтому они непрерывны на отрезке [a, b]. производная = (90) Поскольку f ‘(x) существует, он существует в интервале (a, b). В конце сегмента F (a) = F (b) = 0. На основании теоремы о роли существует точка x = c на отрезке [a, b] с F ‘(c) = 0. На основании уравнения (90): Отсюда Если вам нужно доказать.
Теорема Лагранжа может быть геометрически описана следующим образом: График функции r = / (*) имеет вид Условия теоремы (см. Рис. 146). Отношения представляют Является ли угловой коэффициент струны AB%, соединяющей концы дуги. Поскольку f ‘(c) = tga — угловой коэффициент касательной, теорема Лагранжа показывает, что на графике функции y = f (x) хотя бы точка, в которой касательная графика параллельна хорде, соединяющей концы дуги В нем говорится, что есть один. Уравнение (89) часто переписывается как: f (b) -f (a) = (b-a) f ‘(c). (91) чо равенство выглядит так: Приращение дифференцируемой функции для сегмента [a, b] равно длине сегмента (то есть приращение аргумента, умноженное на производное значение этой функции во внутренней точке сегмента).
Уравнение (91) называется уравнением Лагранжа или уравнением конечного приращения. Пример. Функция f (x) = x * определяется сегментом [0; 1]. Определите значение x, которое делает график касательным параллельно коду, Затяните оба конца дугового графика. Решения. Поскольку f (b) = f (1) = 1 и f (a) = f (0) = 0, уравнение (91) дает 1 -0 = (1 -0) / ‘(c) или f’ (c) = . С другой стороны, так как f ‘(*) = 4×8, поэтому f’ (c) = 4c3, Как известно, производная от константы y -c равна нулю. Используйте теорему Лагранжа, чтобы доказать утверждение.
Если функция теоремы f (x) непрерывна в отрезке [i, b] и имеет производные [‘(x) 0 во всех внутренних точках, то функция f (x) находится в отрезке [a> b] Это постоянно. Доказательство. Пусть x — любая точка в сегменте, соответствующая a. Описывает уравнение Лагранжа (91), примененное к отрезку [a \ x]. j (x) -f (a) = (x-a) / ‘(c). c — точка между aw x. с является отрезком [i; 6], тогда f ‘(c) = 0. Таким образом, для любой точки x в отрезке f (x) -f (a) = 0, то есть f (x) = f (a) [a; b], то есть функция f (x) является отрезком [a \ 6] означает константу.
Результаты Если производные Φ (x) и F (x) двух функций одинаковы во всех точках отрезка [a; 6], то разница между этими функциями в этом отрезке постоянна. Доказательство. Пусть f (x) -Φ (x) -F (x). Далее, по предположению, Ф ‘(х) = F’ (х), поэтому f ‘(х) = Ф’ (а) -Т7 ‘(х) = 0. Следовательно, на основании доказанной теоремы f (x, v) = Φ (x) -> F (x) постоянна в отрезке [a \ b . nmm-] imm * \ (92) Это тф (х)> Lim _ ,,, .. 4.Рубитальные правила * Вы знакомы с тем, как найти пределы отношений между вашей V, двумя минимальными или бесконечными функциями, то есть выявить неопределенность формы ~ и ~. Бу здесь, установить
Мы рассмотрели новое правило, которое раскрывает эти неопределенности, называемые правовыми правилами. Теорема (быстрое правило). Пусть j (x) и η (x) — дифференцируемые функции вблизи точки c, исключая саму точку c, так что x-> c, эти функции равны нулю или бесконечны. В таких Существует ограничение, такое как соотношение их производных | x-> c, Тогда те же ограничения связаны с самой функцией
Я показываю эту теорему без доказательства. Пример 1. Найти lim sm-. Решения. У нас есть Nga «taSj = lim W = lira 5co, sS * = 5 lim cos 5 * = 5. х-о * х- * о х х- + о 1 х- * о
