Оглавление:


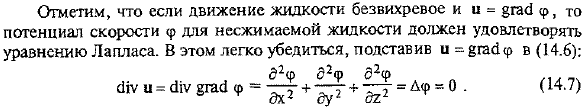

Дифференциальное уравнение, выражающее закон сохранения массы
Дифференциальное уравнение, выражающее закон сохранения массы. Уравнение, представляющее закон сохранения массы контролируемого объема жидкости V, имеет следующий вид: (3-51) представляет форму (14.1), используя выражение субстанциальной производной формы. Чтобы получить искомое дифференциальное уравнение, воспользуйтесь теоремой остроглацкого Гаусса (3.25) для преобразования площади поверхности в объемный Интеграл.
Так как объем V ограничен поверхностью a, неподвижной в пространстве (она не изменяется во времени), то частный дифференциал по времени можно поместить под знаком интеграла. Людмила Фирмаль
- При объединении после этого объемного интегрирования он получается. Так как формула (14.4) была получена для любой области V, то подынтегральное выражение должно быть равно нулю во всех точках пространства, занимаемого liquid. In дело в том, что если в какой-то точке пространства подынтегральная функция не равна нулю, например положительна, то в непосредственной близости от этой точки(если подынтегральная функция непрерывна) значение этого выражения также положительно.
- Принимая эту окрестность за объем V, мы видим, что интеграл (14.4) больше нуля (не равен нулю), что противоречит уравнению(14.4). Поэтому во всех отношениях в пространстве, занимаемом жидкостью. Самое главное, если жидкость несжимаема и ее плотность не зависит от времени или пространственных координат (p = sop $ 1), то частный случай этого уравнения.
Это дифференциальное уравнение, выражающее закон сохранения массы при описании движения жидкости с использованием модели сплошной среды. Людмила Фирмаль
- Уравнение (14.6)называется дифференциальным уравнением несжимаемости. Заметим, что если в движении жидкости нет вихря и u =гаёфф, то потенциал скорости incomp несжимаемой жидкости должен удовлетворять уравнению Лапласа. Это можно легко проверить, подставив u = & gadf в(14.6).
Смотрите также:
Примеры решения задач по гидравлике
Возможно эти страницы вам будут полезны:
- Метод расчета подземного контура, основанный на использовании коэффициентов потерь напора (метод коэффициентов сопротивления).
- Дифференциальные уравнения механики жидкости и газа. Предварительные замечания.
- Дифференциальные уравнения, выражающие закон изменения количества движения (уравнения движения в напряжениях).
- Дифференциальные уравнения, выражающие закон изменения момента количества движения
