Оглавление:
Дивергенция поля. Формула Остроградского-Гаусса
Важной характеристикой векторного поля (71.1) является так называемая дивергенция, характеризующая распределение и интенсивность источников и стоков поля.
Дивергенцией (или расходимостью) векторного поля
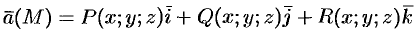
в точке 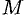 называется скаляр вида
называется скаляр вида 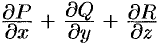 и обозначается символом
и обозначается символом 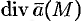 , т. е.
, т. е.
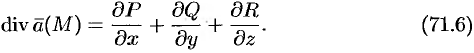
Отметим некоторые свойства дивергенции.
- Если
 — постоянный вектор, то
— постоянный вектор, то 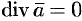 .
. 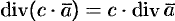 , где
, где 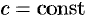 .
.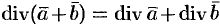 , т. e. дивергенция суммы двух векторных функций равна сумме дивергенции слагаемых.
, т. e. дивергенция суммы двух векторных функций равна сумме дивергенции слагаемых.- Если
 — скалярная функция,
— скалярная функция,  — вектор, то
— вектор, то
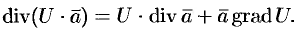
Эти свойства легко проверить, используя формулу (71.6). Докажем, например, справедливость свойства 4.
Так как 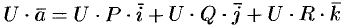 , то
, то
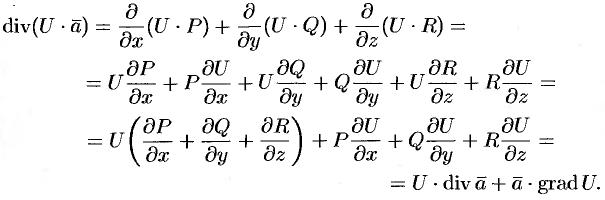
Используя понятия потока и дивергенции векторного поля, запишем известную в анализе (см. (58.9)) формулу Остроградского Гаусса
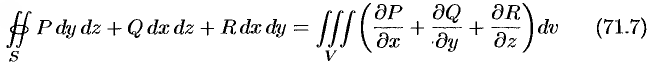
в так называемой векторной форме.
Рассматривая область  , ограниченную замкнутой поверхностью
, ограниченную замкнутой поверхностью  , в векторном поле (71.1), можно утверждать, что левая часть формулы (71.7) есть поток вектора
, в векторном поле (71.1), можно утверждать, что левая часть формулы (71.7) есть поток вектора  через поверхность
через поверхность  ; подынтегральная функция правой части формулы есть дивергенция вектора
; подынтегральная функция правой части формулы есть дивергенция вектора  . Следовательно, формулу (71.7) можно записать в виде
. Следовательно, формулу (71.7) можно записать в виде
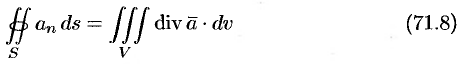
(в котором она чаще всего и встречается).
Формула Остроградского-Гаусса означает, что поток векторного поля через замкнутую поверхность  (в направлении внешней нормали, т. е. изнутри) равен тройному интегралу от дивергенции этого поля по объему
(в направлении внешней нормали, т. е. изнутри) равен тройному интегралу от дивергенции этого поля по объему  , ограниченному данной поверхностью.
, ограниченному данной поверхностью.
Используя формулу (71.8), можно дать другое определение дивергенции векторного поля 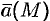 в точке
в точке 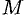 (не связанное с выбором координатных осей).
(не связанное с выбором координатных осей).
По теореме о среднем для тройного интеграла (см. п. 54.1) имеем:
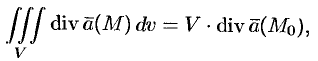
где 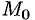 — некоторая (средняя) точка области
— некоторая (средняя) точка области  . Тогда формулу (71.8) можно переписать в виде
. Тогда формулу (71.8) можно переписать в виде 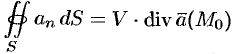 . Отсюда
. Отсюда
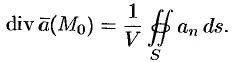
Пусть поверхность  стягивается в точку. Тогда
стягивается в точку. Тогда 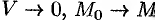 , и мы получаем выражение для
, и мы получаем выражение для 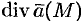 в точке
в точке  :
:
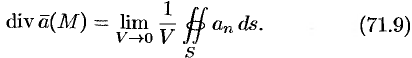
Дивергенцией векторного поля в точке  называется предел отношения потока поля через (замкнутую) поверхность
называется предел отношения потока поля через (замкнутую) поверхность  , окружающую точку
, окружающую точку  , к объему тела, ограниченного этой поверхностью, при условии, что вся поверхность стягивается в точку
, к объему тела, ограниченного этой поверхностью, при условии, что вся поверхность стягивается в точку 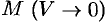 .
.
Определение (71.9) дивергенции эквивалентно (можно показать) определению (71.6).
Как видно из определения, дивергенция векторного поля в точке является скалярной величиной. Она образует скалярное поле в данном векторном поле.
Исходя из физического смысла потока (обычно условно считают; что 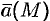 есть поле скоростей фиктивного стационарного потока несжимаемой жидкости), можно сказать, что: при
есть поле скоростей фиктивного стационарного потока несжимаемой жидкости), можно сказать, что: при 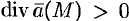 точка
точка  представляет собой источник, откуда жидкость вытекает; при
представляет собой источник, откуда жидкость вытекает; при 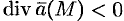 точка
точка  есть сток, поглощающий жидкость. Как следует из равенства (71.9), величина
есть сток, поглощающий жидкость. Как следует из равенства (71.9), величина 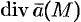 характеризует мощность (интенсивность, платность) источника или стока в точке
характеризует мощность (интенсивность, платность) источника или стока в точке  . В этом состоит физический смысл дивергенции.
. В этом состоит физический смысл дивергенции.
Понятно, что если в объеме  , ограниченном замкнутой поверхностью
, ограниченном замкнутой поверхностью  , нет ни источников, ни стоков, то
, нет ни источников, ни стоков, то 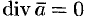 .
.
Векторное поле, в каждой точке которого дивергенция поля равна нулю, т. е. 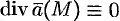 , называется соленоидальным (или трубчатым).
, называется соленоидальным (или трубчатым).
Пример №71.4.
Найти дивергенцию поля линейных скоростей 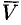 жидкости, вращающейся как твердое тело вокруг неподвижной оси с постоянной угловой скоростью
жидкости, вращающейся как твердое тело вокруг неподвижной оси с постоянной угловой скоростью 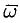 .
.
Решение:
Примем ось вращения жидкости за ось 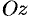 . Тогда, как показано ранее (см. пример 69.2),
. Тогда, как показано ранее (см. пример 69.2), 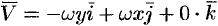 . Имеем:
. Имеем:
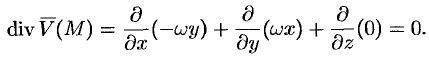
Поле 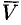 — соленоидальное.
— соленоидальное.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Интеграл Фурье |
| Градиент скалярного поля и его свойства |
| Циркуляция векторного поля |
| Ротор векторного поля. Формула Стокса |
