Оглавление:







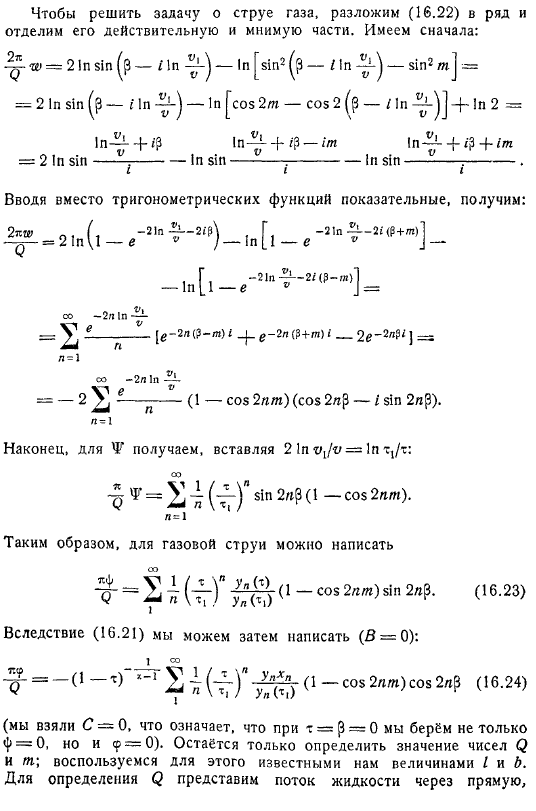


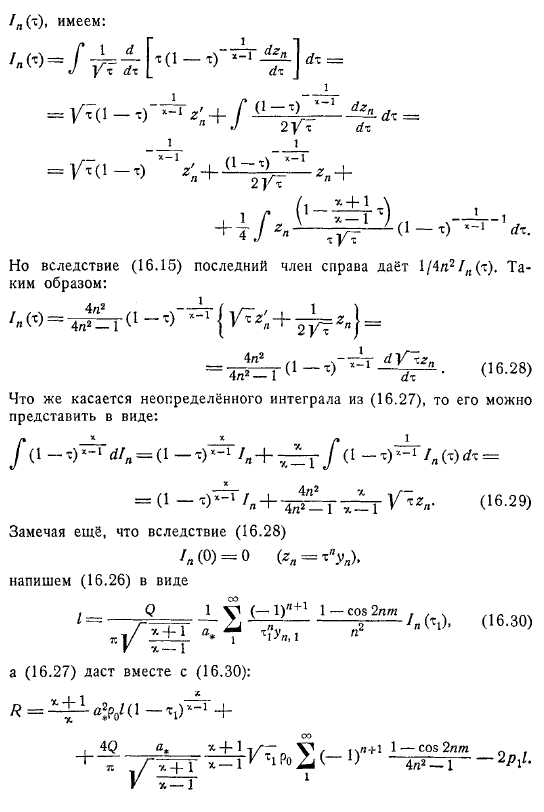




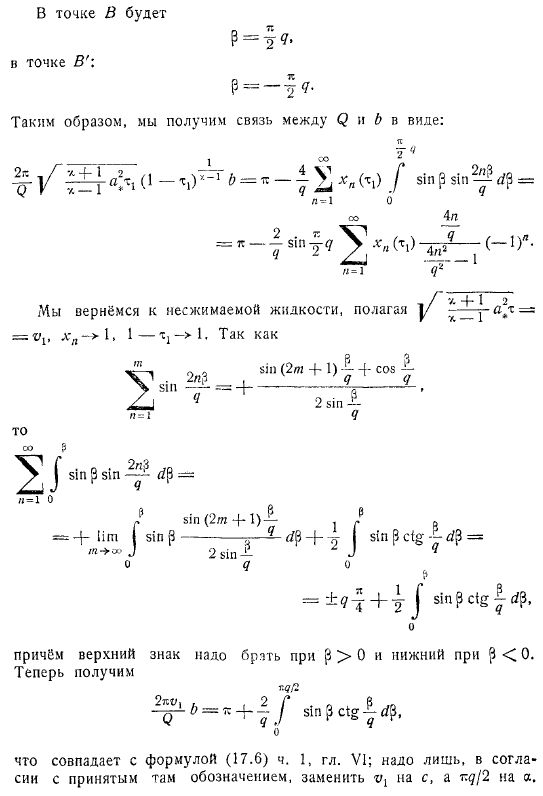


Дозвуковые скорости. Теория Чаплыгина
Дозвуковые скорости. Теория Чаплыгина. Примеры. Эти решения были даны в замечательных работах Чаплыгина, содержащих обобщения теории струй Кирхгофа — Жуковского на случай безвихревого движения сжимаемой жидкости.
Имеем безвихревое движение и берём уравнение Бернулли в виде: где р = const, вследствие отсутствия вихрей. В формуле пишем (иная нумерация линии тока) Введём потенциал скоростей: оставим в качестве искомых функций, но введём в качестве независимых переменных вместо координат х и у величину скорости v и угол наклона скорости по отношению к оси Ох. В этом и заключается преобразование Чаплыгина.
Смотрите также:
Решение задач по гидромеханике
Решая эти уравнения относительно dx и dy, получим. Это значит, что воспользовавшись второй из формул для выражения dq. Интегралы, входящие в уравнения легко вычисляются. Что же касается неопределённого интеграла из , то его можно представить в виде. Замечая ещё, напишем в виде, легко видеть. Получим окончательно где по-прежнему плотность позади пластинки.
Напомним, что приходится определять из после того как q известно. На пластинку набегает поток бесконечной ширины, мы получим, очевидно. В качестве второго примера рассмотрим истечение газа из бесконечно широкого сосуда.
Пусть давление во внешнем пространстве есть рх, давление внутри сосуда, на бесконечности, там, где скорость v=0. Обозначим ширину отверстия , а угол, который составляют стенки с осью,получим истечение из сосуда, у которого стенки служат одна продолжением другой. Для соответствующей задачи в несжимаемой жидкости мы будем иметь и далее.
Ряд этот абсолютно сходящийся, и, применяя формулу, получим для функции тока, определяющей истечение сжимаемой жидкости из того же сосуда и при той же скорости на струе. Потенциал скоростей по запишется в виде, остаётся только определить. Чтобы сделать это. Найдем, как меняется у вдоль струи. Определим сперва вообще у как функцию от х до р.
Так как при р = 0 мы должны получить у = 0, то следует считать. Вдоль линии тока имеем: второй из интегралов, стоящих справа, легко вычисляется. В самом деле, так как по известной теореме тригонометрии причём знак плюс надо брать, когда у > 0, и знак минус, — когда Таким образом, мы получим связь в виде.
Определим ещё «сжатие струи» в сжимаемой жидкости. Будет иметь место в бесконечно удалённой части струи (иначе скорость получила бы максимальное значение где-нибудь внутри струи). Если ширина бесконечно удалённой части струи будет, то нужно помнить, что движения, о которых мы говорили в этом параграфе, совершаются с дозвуковыми скоростями, в частности, в нашей задаче о струе, максимальные скорости не должны превосходить скорость звука, т. е. должно быть что эквивалентно условию в одном из следующих параграфов мы рассмотрим обратный случай.
Представляя по уравнению Бернулли будем иметь, так как по Уравнения решают вопрос о движении газа, если известна область переменных х, р, отвечающая этому движению, если цано со своими первыми производными конечна, однозначна и непрерывна, наконец, если всегда будет и только в отдельных точках контура области может быть.
Остановимся на доказательстве определённости вида функции, удовлетворяющей указанным условиям. Применим доказательство от противного: пусть есть две функции, удовлетворяющие нашим требованиям; покажем, что функция в данной области конечна, непрерывна, удовлетворяет уравнениям и обращается в нуль на контуре.
Умножим на и проинтегрируем по всей нашей области . Обозначая результат интегрирования через, получим без труда где двойной интеграл распространён на всю площадь однократный— на её контур.
Но на контуре будет , значит, равенство может иметь место лишь при условии равенства нулю двойного интеграла, а при высказанных выше условиях подынтегральная функция в этом интеграле не может быть отрицательной. Ясно, что надо принять эту подынтегральную функцию равной нулю, так что внутри области будет везде
Переходя к движениям, происходящим со всюду дозвуковыми скоростями, мы начнём с точных решений, получаемых в явном виде. Людмила Фирмаль
В работе С. А. Чаплыгина доказывается, на основании . Что рассматриваемые как функции координат х, у, не имеют. Отсюда видно, что если всюду будет решение уравнения. Положим теперь: мы получим для определения уравнение. Это есть известное уравнение для гипергеометрического ряда.
Составляя характеристическое уравнение для показателя р в области. Сохраняя то решение, которое остаётся конечным при , мы будем иметь, пользуясь обозначением Гаусса: Посмотрим теперь, какие из задач указанного выше типа могут быть решены при помощи функции где пробегает счётную последовательность возрастающих.
Смотрите также:
Так как газовая струя ограничена линиями тока, то вдоль контура области функция должна принимать те или иные постоянные значения. При этом, если рассматриваемая часть контура отвечает плоской стенке, то вдоль неё ; если же речь идёт о свободной поверхности, то там будет, и по уравнению Бернулли .
- Сравним теперь нашу задачу с задачей о течении несжимаемой жидкости при тех же граничных условиях, т. е. При том же расположении стенок, при тех же скоростях в бесконечности и при тех же скоростях на границе струй. Задача о струйном течении несжимаемой жидкости была решена по методу Жуковского в части 1.
Следуя этому методу, найдём связь между переменными где потенциал скоростей и функция тока в соответствую¬щей задаче о несжимаемой жидкости. Пусть мы получили предположим, что может быть разложена в ряд вида. Наша задача о течении газа разрешится тогда формулой: есть гипергеометрический ряд имеют как раз те значения, которые входят. В самом деле,правые части совпадают.
Задача о струйном течении несжимае¬мой жидкости была решена по методу Жуковского Людмила Фирмаль
Далее, если при каком-нибудь значении р функция, определяемая не зависит от т, то это будет лишь, если при всяком, участвующем в сумме. Но тогда и правая часть будет постоянна при том же р. Таким образом, будет удовлетворять граничным условиям задачи. Формально удовлетворяет уравнению.
Таким образом, если ряд будет сходиться при всяком будет стремиться к тому же пределу, что и ряд (, причём не только ряд , но и ряды, составленные формально путём его почленного дифференцирования по х и р, будут сходиться абсолютно и равномерно, то мы вправе считать, что частные производные.
