Оглавление:





Движение точки, притягиваемой двумя неподвижными центрами, обратно пропорционально квадрату расстояния
- В случае плоского движения задача о движении точек, притянутых к 2 неподвижным центрам с силами, обратно пропорциональными 2 квадратам расстояния, была впервые сведена Эйлером к квадратуре. Лагранж предложил общее решение, и Якоби объединил его с методами интеграции, описанными в этой главе. Квадратура эллиптичности, найденная в Интеграле, дала важный пример для применения лежандром теории эллиптических интегралов.
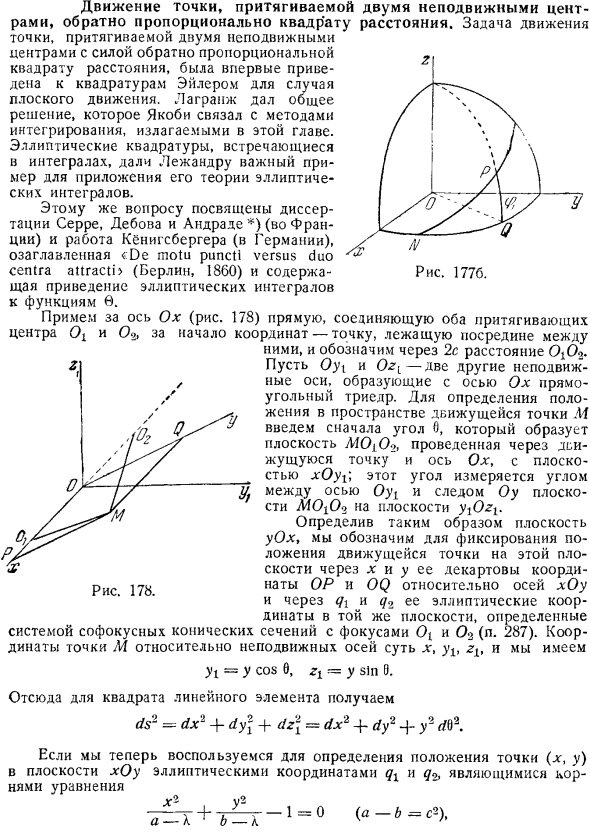
Тезис Серра, Дебова, Андраде Франция и исследование Кбнигсбергера Германия Берлин, I860, озаглавленное De motu puncti vs duo centrar ti , содержит редукцию эллиптического интеграла к функции 6. Возьмите ось Ox рис. 178, прямую линию, которая притягивает оба Oz в качестве начала координат, точку в середине их и 2C, чтобы указать расстояние OjOo. Пусть Ouh и OzL это другие 2 неподвижные оси, которые образуют ось Ox и прямоугольник trihel.
Этот результат ясен и геометрически, так как действительное перемещение точки происходит не по касательной к движущейся кривой и работа реакции не равна нулю. Людмила Фирмаль
To определив положение в пространстве движущейся точки M, сначала введем угол 0, который образует плоскость O1O1O2 через движущуюся точку и ось Ox, в плоскости xOy1.Этот угол измеряется углом между осью Oyt и локусом AfOjOo на плоскости трассировки плоскости у О. Определив таким образом плоскость yOx, фиксируем положение движущейся точки На этой плоскости по квадратурным координатам OP и OQ для x и y на оси xOy, а qx и q в той же плоскости, определяемой системой конфокальных конических сечений QX и q ее фокусом эллиптичности O и O3 с. 287.Координаты точки M для фиксированной оси X, yx, zb, YX = y COS0, Zi = y sin 0.
Отсюда, для квадратного линейного элемента DS2 у = dx2 4 4 почтовый индекс dy2 dz2 = dx2 4 почтовый индекс dy2 4 У2 rfO2 при использовании эллиптических координат qx и q2, являющихся корнями уравнения, для определения положения точки x, y в плоскости xOy оно выглядит следующим образом: Затем, согласно ранее установленной формуле пункт 287 + ды = л Nxdq + Н dqfy Ш = a x 6 x. Итак, в рассматриваемой системе координат квадрат линейного элемента равен = Т Л + Л + У2 D02 в Где Ni, N2 и No должны быть заменены выражением через qx и Hb выше. Получите массу очков за единицу. Тогда кинетическая энергия равна T = Y S 2 = + 2 + 4 а 2 Где 0 и 0 служат параметрами Q2 и q z.
Если r2 представляется расстоянием от движущейся точки до обоих фокусов, то алгебраические значения гравитационных сил со сторон этих фокусов равны и, а сумма равна r2r2 Два Эти рудиментарные работы 7 r общая разница в мощности G1 G2 Особенности 4. адрес. Г1 2 Но так как квадрат полудлинной оси эллипса через точку AL равен a qit, то сумма расстояний r r2 от точки M до обоих фокусов равна р ж п Р2 = 2 е ц. Аналогично, площади горизонтального половина оси гиперболы, проходящей через точку автофокусировки равняется В2 Г1 Г2 = 2 Р Здесь. И уя Q Т 4 В а Q2 и R2 = в А Г В а м.
После приведения его к общему знаменателю Четыре Р2 22 11. Для краткости = Н + П А ФЛ + FX2 с Г Р Так что Ui зависит только от U2 зависит только от q2y. где вспомогательные переменные p, p3 являются частными производными от T на q V q T и O. й 4 ПТ = 4 jV2 2 Pz = Нет. если мы решим эти уравнения относительно q v 4 и о и присвоим их Гамильтоновой функции U = T U: 2×21, 2х, J Обратите внимание, что вы можете заменить Nb N2 и y2 значениями функций qt и q2 и записать: 1 А Б в 1 У2 = г Б К2 ц б б 2К Наконец, функция H представлена в следующем виде = rY2 1 2 Р Р3 + Ут. Теперь вы можете легко описать уравнение Якоби. Подставляя V = ht 4 W7, предыдущее стр.
- Здесь это зависит только от qb и beta2 только от q2. Дело в том, что если вы присвоите эту формулу 1G предыдущему уравнению и освободитесь от знаменателя, то для определения R2 вы получите уравнение, которое можно описать в виде: Правая сторона зависит только от qit, а левая только от q .Поскольку параметры QT и q являются независимыми переменными уравнений в частных производных, единственный способ удовлетворить это последнее отношение без установления отношения между ql и q2 это сделать каждую часть индивидуально равной одной и той же константе 2 Затем и решите уравнение, установленное с уважением.
Эти выражения находятся в квадратуре И Определите и получите выражение для требуемого полного интеграла + 7 + 7Ди Два Любой из 3 х постоянных а, 3 и А, ни один из которых не являются аддитивными. Чтобы получить траекторию, вы должны использовать, если и и K д 7и О А Б — J 4 b qOV SJtqO — А Б а. 4 ля Г… + Г Джей Vifoh Дж Т установление связи между q и q2 2 е из этих уравнений представляет собой относительную траекторию движения плоскости xOy, а первое уравнение определяет угол поворота этого plane. To получаем время, приравниваем частные производные U0 относительно h разности t 7. 1 G 4i dqx 1 q. dq.
Три дифференциальных уравнения, которые мы установили для этой кривой, приводятся, 1 как мы видели, к двум. Людмила Фирмаль
Таким образом, задача сводится к квадратуре. Эти квадратуры являются эллипсами и qx a = s и q. as вы можете видеть, установив a= , это имеет смысл по отношению к s2. Для формул вспомогательных переменных p , p , p3, необходимо взять частную производную IF относительно q , q2, 0, чтобы найти их. Л = Тиг Л = Л ПЗ = с Последнее выражение проясняет значение константы a. In факт, из уравнения, которое определяет p3, p3 = y2b стр. 874 был obtained.
Интеграл= a равен Y20 В = = а поскольку y и 0 являются полярными координатами проекта, они представляют возможность применения закона площади к проекции движения на плоскость Положение точки движения на этой плоскости. Эту ситуацию можно было предсказать заранее, так как сила, действующая на точку, пересекает ось Ox. Если начальная скорость точки пересекает ось Ox, то локус явно находится в плоскости AljOtO, определяемой начальным положением точки и центром притяжения обоих. Это можно увидеть из equation. In дело в том, что в этом случае константа а будет равна нулю, и первое уравнение траектории 7 будет таким: это указывает на то, что плоскость уОх остается неподвижной.
Уравнение T определяет орбиту эклиптики. Интеграл уравнений Эйлера. предположим, что это = n2= 0, а не просто a = 0.поскольку плоскость yOx неподвижна, траектория плоская, и нет никакой силы, эта траектория становится прямой линией на плоскости yOx. При этих предположениях 2 я часть уравнения T после замены f qO и f q выражается в выражении Я 2 O fg J Джей 1 а j =р 42 б д г Поэтому это уравнение представляет собой прямую линию и может быть идентифицировано линейным уравнением в эллиптических координатах.
Это очевидно алгебраично в терминах Qi и q2.In таким образом, следуя Лагранжу, мы воспроизвели очень важный результат, который дал Эйлер, выразив, что уравнение E признает алгебраический Интеграл. Добавление эллиптических функций основано на этом результате. Заметим аналогично, что в координатах, которые мы используем, мы можем вывести задачу о движении точки под действием силы с функцией силы следующего вида к квадратуре. Ут ОО.
И1 мне Здесь произвольная функция переменной qi только и 1L является функцией переменной q2 только. Например, силовая функция этой формы, для предыдущей силы притяжение к неподвижному центру Oi и O3 по закону обратной пропорции к 2 му расстоянию, хранится в кубической обратной функции притяжения yjo i, которая пропорциональна расстоянию и перпендикулярна плоскости, с притяжением к кубу, с притяжением к поверхности. В заключение следует отметить работу Верде ber ein einen Speciale f r f hrleuhr von zweienschaften Berlin, P.
Смотрите также:
Решение задач по теоретической механике
| Геодезические линии поверхностей Лиувилля. Приложение к эллипсоиду | Эллиптические координаты в пространстве |
| Движение планеты в сферических координатах по Якоби | Наименьшее действие. Свободная точка |
