Оглавление:









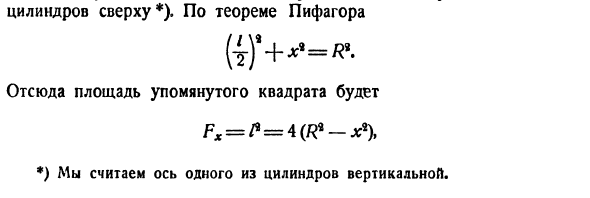

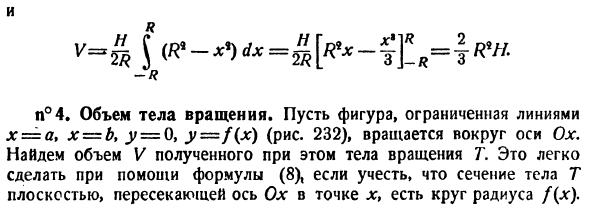







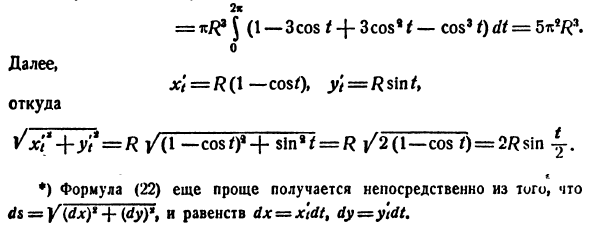

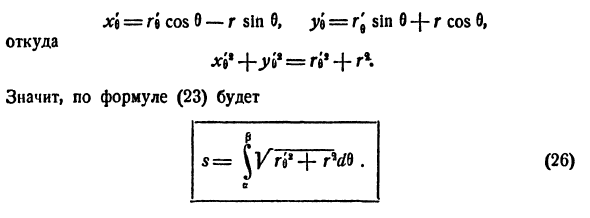



Геометрические приложения определенного интеграла
Конкретные геометрические приложения интеграции № 1. Расчет площади. Декартовы координаты. Расчешите для вычисления площади F изогнутой трапеции, окруженной линиями x = a, x = b, y = 0, y = f (x)> 0. «F равно целому б (О но Уравнение (1) обычно б (2) но Обратите внимание, что y следует заменить формулой f (x) из уравнения граничной кривой. Обратите внимание, что уравнения (1) и (2) могут быть легко получены с использованием предыдущего метода.
- Таким образом, r = jjX и для объема V конуса вы получаете известную формулу о 2) Объем мяча такой же простой. Радиус круга, заштрихованного рисом, r, 229, который является сечением шара от плоскости x (-R ^ x ^ R) равно VR * -x \ из теоремы Пифагора как Линия -xm * = * (φ-x *), Следовательно, объем мяча составляет R 3) Объем общей части двух цилиндров. Убедитесь, что оси двух цилиндров с одинаковым радиусом R пересекаются под прямым углом.
Найдите объем V объекта T, где пересекаются цилиндры. Немного трудно ясно увидеть это тело, но оно нам не нужно. Пусть P — плоскость, содержащая оси обоих цилиндров. Если T параллельна P и разделена плоскостью на расстоянии x от P (эта плоскость пересекает каждый цилиндр определенной полосы. Поскольку эти полосы явно одинаковы, пересечение T и плоскости Является ли квадрат, и I сторона этого квадрата проста, из рисунка 230.
Для оси Ox возьмите прямую линию, перпендикулярную плоскости P и проходящую через пересечение осей обоих цилиндров. Людмила Фирмаль
Верхний цилиндр *). По теореме Пифагора (4) 4 * — *. Отсюда площадь упомянутой площади *) Одна ось цилиндра считается вертикальной.И формула (8) R Интересно, что ответ не включает в себя иррациональность. 4) В качестве последнего примера рассмотрим так называемый цилиндрический сегмент, корпус 7 *. Он отделен от цилиндра плоскостью, проходящей через диаметр основания. Давайте использовать обозначения на рисунке. 231 — это AB = H, OA = R.
Если тело T пересекает плоскость, параллельную плоскости треугольника OAV (сечение получает треугольник OxAxBx, как в OAV, если 00i = x {-R ^ x ^ R),% треугольник 0 \ AxBx равен Fx ^ OxAvAxBx. Однако согласно теореме Пифагора OtAi = Un * -FIG. И из сходства треугольника OAB и 0 \ Afx, AHB {_OlAt AB-OA 9 где и -R № 4. Вращение объема тела. Поверните фигуру, заключенную в линии x = a, x = b, y = 0, y = f (x) (рис. 232), вокруг оси Ox. Найти объем V вращающегося тела T, полученный в этом случае. Учитывая, что поперечное сечение тела T плоскостью, пересекающей ось Ox в точке x, является окружностью с радиусом f (x), это легко сделать с помощью уравнения (8).
Поэтому *) и б V = ii \ f * (x) dx. Обычно это уравнение (9) Пример. Объем объекта, образованного вращением вокруг оси Ox фигуры, окруженной осью Ox и полуволновой синусоидальной волной (рис. 220) y = sin * (Oh ^ x ^ i) хорошо T / G. o J f 1 —C0v2dg. x g sta2xl » sin * xdx = «^ -2 — dx =? [x-2-Jo = y Замечания. Линия y = a, y = b9Λ? = 0, x = f (y) (рис. 233), фигура, окруженная осью Oy, вращается, а затем объем V Рисунок 233. Рисунок 232.
- Полученный ротатор находится по аналогичной формуле б y = ic \ x * dy> но — Где х есть ф (у \ •) Для простоты мы предположили, что f (x) ^ 0. Понятно, что уравнение P1 = * / * (x) также верно, когда f (x) меняет знак.
Пример. Предположим, что параболическая дуга y = ax (a> 0), разрезанная прямой линией y = h> 0 (рис. 234), вращается вокруг оси Oy. Согласно уравнению (10), результирующий объем объекта (называемый вращающимся параболоидом) равен Ах ах Принимая во внимание точку параболы, отмеченную на чертеже, можно дать четкое объяснение этого результата. Его абсцисса r и ордината h связаны соотношением h = ar .
Таким образом, V == T * 4h = -j * rVt ‘Рисунок 234. Однако 1cr * A — объем цилиндра с радиусом r и высотой A, за которым следует теорема Архимеда. . № б. Длина дуги кривой. Рассмотрим проблему длины гладкой дуги s. y = f (x) (a ^ x ^ b). Выберите основной сегмент дс от дуги. Этот отрезок можно считать почти прямым, потому что кривая гладкая **). Применяя теорему Пифагора к заштрихованному треугольнику (рис. 235), вы можете найти ***.
Объем вращающегося параболоида равен половине объема цилиндра с таким же радиусом основания и высотой Людмила Фирмаль
ds = V (dx? + (dy) \ Ho dy = y’xdx. смысл ds = VT + ySd * и L 8 = \ VT + *} dx% но Где y’x = f ‘(xy Рисунок 235. •) Помните, что кривая называется гладкой, если все ее точки имеют касательные, которые непрерывно изменяются вдоль касательной. В частности, если существует непрерывная функция f (x), кривая = = / (q) является гладкой. Последнее также предполагается в этом n \ — **) Напомним, что этой строке соответствует гладкая изогнутая минимальная дуга. ***) Строго говоря, вертикальная нога треугольника равна Du, но замена Du на dy9 допускает меньшую ошибку порядка.
Пример. Найти длину кривой дуги Эта кривая называется астроид *) и имеет изображение, показанное на рисунке. 236 видов бриллиантового туза. На самом деле, прежде всего, обратите внимание, что кривая симметрична относительно обеих осей (потому что x и y попадают под знак квадратного корня куба) x: X * ‘* = yfx *). Сечение кривой в первом квартале имеет следующее уравнение: у = (рупий / (14) Поскольку x может изменяться только от 0 до R, это соответствует уменьшению y с R до 0. От х (14) Это y’x = \ (/? ‘/, — * «/,)’ /. | | D.-v.) f y’x = — (R * / i-X * ‘*) 4 * X до H (15)
Это показывает, что кривая является гладкой (для этих х Дифференциация идет непрерывно). Если x = R, yx = 0, если x- + 0, y’x- + -oo / Таким образом, астроид касается обеих осей. С (15) y = (# * / «-A; * /,) x-Chr = K1 * X-% 1r-I. Таким образом, длина дуги в первой четверти составляет: R __R Следовательно, общая длина астроида s: s = 6R. Рисунок 236.
dF = ydx. Осталось суммировать * Уравнение (3), чтобы получить (2). Пример. Найдите область, окруженную полуволновой синусоидой (рис. 220). (2) Согласно » F = \ sin xdx = [-cos xR = 2.о Рисунок 219. (3) G J £ HFF * L в Используйте метод из предыдущего абзаца. Конечно, если на фигуре заштрихованы 219 базовых полос, получим базовый прямоугольник dx и высоту y.
Его площадь Интересно, что эта величина проще выражается в R, чем окружность 2 м. = 6,283 … р. *) Имеет кинематическое происхождение. Когда круг вращается без скольжения внутри фиксированного круга большего радиуса, каждая точка представляет собой линию, называемую гипоциклоидой. Астроид — это гипоциклоид с радиусом 4. Линия, описываемая точкой круга, катящегося по внешней стороне неподвижного круга, называется эпициклоидой. Все эти кривые используются в теории зацепления.
N ° C. Площадь поверхности вращения. Поверните плавную кривую дуги y = f (x) ^> 0 (a ^ x ^ b) вокруг оси Ox (Рисунок 237). Найдем площадь L вращающейся поверхности, полученную в этом случае. Для этого выберите из дуги элемент ds, соответствующий изменению абсциссы с x на x + dx. Как мы уже сделали, если мы возьмем этот элемент как прямую линию, часть поверхности, описываемая им, станет усеченным конусом, где ds действует как генератор. Нижний радиус этого конуса y и y + dy.
Следовательно, боковая площадь *) равна ^ Lv + Cy — \ — dy) \ ds = 2ity ds — \ — ndyds (16) Я знаю, что могу игнорировать бесконечно малые числа при вычислении элементарных членов с использованием определенного интеграла Заказать. (Для бесконечно малых dx, dy, ds) Произведение dy ds равно Рисунок 237. Рисунок 238. Бесконечно меньше (16) можно игнорировать, (16) дл = 2 * ярдов (17) Но (12) _ ds = VT + y ^ dx. Отсюда и (17) (18) L = 2 * \ yV \ Ty? Dx,
Где y = f (x) и y’x = f ‘(x). Пример. Найти площадь L поверхности, образованной астроидом xX / * + Y =, вращающимся вокруг оси Ox. Решения. Мы уже обнаружили вышеупомянутую астроидальную дугу. Это в первом квартале, y = (Rt / * -Xi ‘*)’, i> Vl + y’x = Rl / 9x-t / 9- *) Запомните боковую область сгенерированного конуса (рис. 238) и радиусы основания r и Y. * Равно (r + /?) /.
Где y = f (x) и y’x = f ‘(x). Пример. Astroid xX / * + Y = найти площадь поверхности L, образованную вращением вокруг оси Ox. Решения. Вышеупомянутая астроидальная дуга уже была обнаружена. Это в первом квартале. y = (Rt / * -Xi ‘*)’, i> Vl + y’x = Rl / 9x-t / 9- *) Ссылаясь на боковую область сгенерированного конуса (рис. 238) и радиус основания r Пожалуйста и Y. * Равен (r + /?) /.
Применимо, когда кривая интереса задается параметрическим уравнением x-x (t), y = y (t) (jXt ^ q), Кроме того, увеличение t от p до q соответствует увеличению от x или a до b. В уравнении (20) требуется замена x = x (t \, y должна быть заменена на y ((). Ограничения a и b должны быть заменены на p и q.
Длина дуги и площадь поверхности вращения б б в в Перестановка x = x (f) означает перестановку Yl- ^ m, dx = x (dt9 xt Где *) V \ + yUx = V xt * + уt * dU (22) Уравнение (21) принимает вид (23) q __ р 9 _ I = 2ic $ j / p (24) Пример. Найти значения F, V, s и L одной арочной циклоиды. = —Sin0 ”= — может быть решением. Очевидно, dx = R (1-cos ty 2% R 2 * ^ ydx, ==: ^ /? ‘(1-cos t) 4t = 2 раза = /? «Jj (l-2cos f + j _ Как хорошо V = w jj (l-cosO’rf ^ О,
2g = * R * J (1-3 cos t -f 3cos * 1-cos31) dt = 0 К следующему ΛG / = /? (1 — cos /), y’t = Rs \ ntf Откуда ^ Xta + y’t ‘= R / (1-cosOa + s! Na / = R / 2 (1-cos /) = 2Rsin y. и ♦) Уравнение (22) получается непосредственно из </ s = Y (</ g) * + Jdyp9 и уравнения dx = фx \ dt% dy — y \ dt.
смысл 7р s = 2R ^ sin y dt = 4R [-cos ^] ^ = SR. о в конце концов 2к 1 = 2 * Дж / *, 2 * 2 * = 4 * /? * ^ (1-cos t) sin ± dt = 8kR * ^ sin8 Если f заменить на 2 <p, * 1 = 16 * /? * ^ Sin8 <p rff = * = -16nR ‘^ (1-cos’ <p) d (cos <p) = -16rcR4 [cos <p-64 И, наконец, L = -g- to /? 1. Следовательно, Z7 = 3 «/? 4, V = 5 ** /?, 5 = 8R, L = n ° 8. Длина дуги в полярных координатах. Предположим, нам нужно найти длину дуги кривой r = f (0), соответствующей интервалу a p. При переходе к декартовым координатам по формуле x = r cos 0, y = r sin 0, (25)
Далее, соотношение (26) (r означает / (0)) представляет собой параметрическое уравнение кривой, а роль параметра играет угол 0. В этом случае xl = g (cos 0-g sin 0, ye = sin 0 -J- r cos 0, Откуда х? + у? = n * + r \ Следовательно, согласно уравнению (23) (26)
Пример. Найти длину кривой r = a (1 + cos c) (i> 0, 0 ^ 0 <2m :). Эта кривая (называемая кардиоидной) имеет форму, показанную на рисунке 5. 239 *). с того времени G8 == — грех 0, тогда ril- | -r, = a * (sini0- | -1 2cos b -f-cos®0) = = 2a * (1 + cos 0) = 4a * cos4— • так 2 * __2k s = j] Aa9 cos% -jdQ = 2a jj cos- | 0 и для A <[0 ? = -A. Функция cos4- Рис 2 г 239. Становится положительным в сегменте [0, mf] и отрицательным в сегменте [mf, 2m]. Итак, правильное решение: 2 * = j Ycos9 для d0 + J | / ^ 4a9 cos9-J </ 0 =
Обратите внимание, что уравнение (2) используется только тогда, когда кривая y = f (x) находится на оси Ox, то есть f (x)> 0. £ _dn Рисунок 221. (Рис. 221) Если f (x) <^ 0, площадь заштрихованной полосы равна dF = —y dx (поскольку площадь положительная, ajf <[0) б у-sinz Рисунок 220 (4) о Наконец, если линия x = a, x = b, y = 0, y = / (*) и кривая y = f (x) должна найти область формы, которая пересекает ось Ox, то сегмент [a , B] делится на части, где f (x) не меняет знак, и l применяется к каждой части соответствующего выражения (2) или (4). Пример.
Найдите область фигуры, заключенную в линию y = 0, y = 6x-bx \ x = 3. Решения. Интересующие нас диаграммы заштрихованы диаграммами. 222 показано, что парабола y = 6x-3x * точно пересекает ось Ox = 2a ^ cosy <20-2a? потому что и » Откуда s = 4a [sin yj * -4a [sin yj2 * = 4a -f-4a = 8a. *) Кардиоида — это особый тип эпициклоиды, где радиус неподвижных и вращающихся кругов равен. Рис. 239. Фиксированный круг представлен слева, а кардиоида — точкой L. 12 И.П. Натансон
max jc = u и x = ‘i. Слишком мало, чтобы согреться, 2 секунды F = \ ydx- \ ydx = 2 3 = \ (6x-3x *) dx- \ (6x-dx *) dx. Итак, F = 8. $ (6x-3x *) dx = [3x * — = 4, o 5 (6x-Z * 4) dx = [Ev: 4-jc®] | = -4, но Рисунок 222. № 2. Расчет площади. Полярные координаты. Нарисуйте два радиуса под углом a (радиан!) От центра круга с радиусом R. Полученная таким образом площадь сектора (рис. 223),
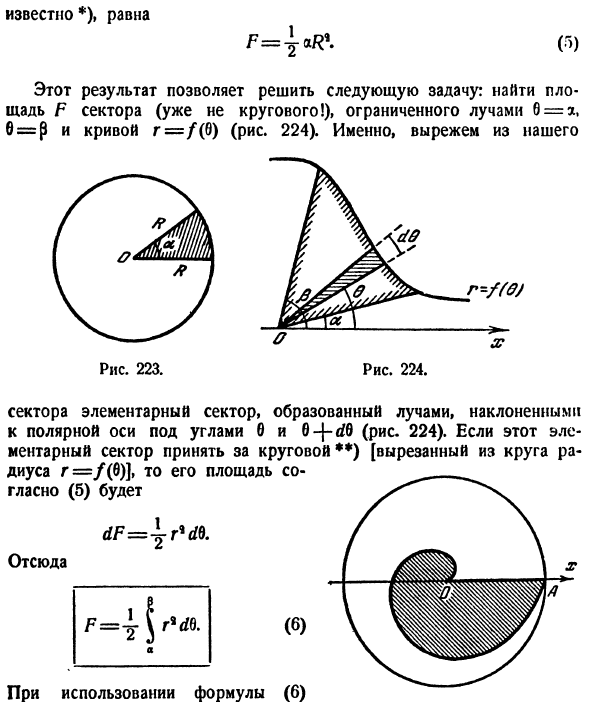
Известный *) равен Этот результат решает следующую проблему: окруженный лучами 6 = a, b = p и кривой r = f (b), чтобы найти веерообразную область F (которая больше не является круглой!) (Рис. 224) , Собственно, мы Рисунок 223. Рисунок 224. Основной сектор образован пучком, наклоненным относительно полярной оси под секторальными углами 6 и — (рис. 224). Если этот основной сектор является круглым **) [вырезан из круга с радиусом r = / (0)], его площадь равна _ Публично (5) / Отсюда При использовании формулы (6)
Необходимо заменить r на функцию / (6). Рисунок 225. Введите уравнение r = f (b). Пример. 1) Найдите область фигуры, ограниченную полярной осью и первой катушкой архимедовой спирали r = kb (рис. 225). •) Однако уравнение (5) ясно. Ясно, что область интересующего сектора является частью той же области круга, что и дуга сектора. Составьте окружность, то есть ^ t-2 ^ 7? » • *) Вы можете быстро увидеть, что ошибки, вызванные этим, бесконечно малы на порядок выше, чем область элементарного сектора.
Решения. Где а = 0, $ о По результатам можно сделать четкое заявление. Другими словами, точка A на пересечении спиральной и полярной осей является радиус-вектором OA = r = k •. Следовательно, площадь круга с радиусом OA равна * OL, = 4 £ 9 * 3. Сравнение этого равенства с (7) дает предложение, все еще открытое Архимедом. Первая катушка полярной оси и архимедовой спирали равна 4 Рисунок 226.
Площадь круга с радиусом, равным максимальному вековому радиусу тора, точки вращения. 2) Найдите область F на фигуре в окружении лемновских коньков Решения. Даже в первой главе полярные координаты показали, что есть g «= a * cos 20. Лемницкое катание симметрично относительно обеих осей, и его часть под первым координатным углом находится между лучами 6 = 0 И 0 = ^ -. Таким образом, с площадью лица, окруженного этой частью Лемнице катание на коньках Равен оси О (заштрихован на рисунке 226) хорошо 1 T cos20 </ 0 = J [sin20] o4 Следовательно, F = q *. хорошо 4
№ 3. Представление объема тела всей площади раздела. (Рис. 227) Поместите объект T между параллельными плоскостями x = a и x = b. Нарисуйте плоскость, параллельную приведенной выше, и пересекающую ось Ox в точке x. Площадь рисунка обозначена Fx. Это сечение тела T этой плоскостью. Рассмотрим базовый слой объекта T, расположенный между плоскостью, пересекающей ось Ox в точках x и x — * — dx. Если этот слой является цилиндрическим, это пластина толщиной dx и имеет площадь F # в нижней части.
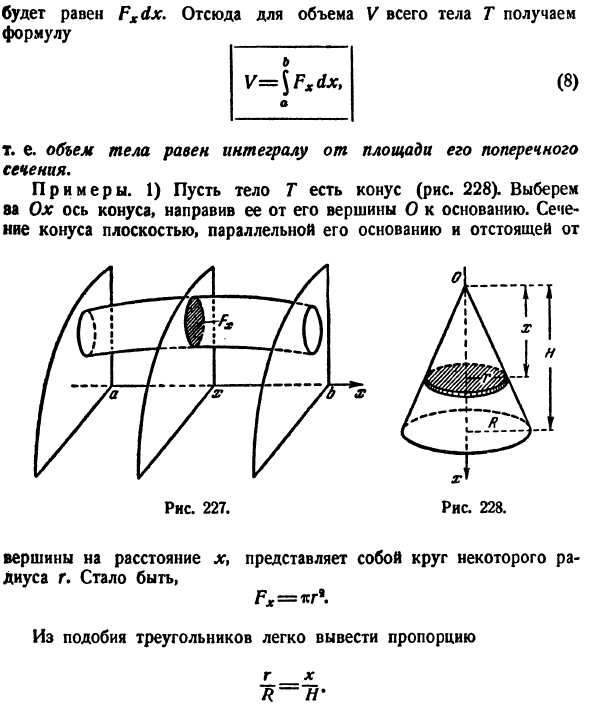
Следовательно, объем d V этого слоя Равно Fxdx. Отсюда для объема V всего тела T формула (8) То есть объем тела равен интегралу его площади поперечного сечения. Пример. 1) Превратить объект Γ в конус (рис. 228). Давайте выберем ось конуса и начнем с вершины O до низа. Коническое сечение параллельно дну и отделено от плоскости Рисунок 227. Вершина на расстоянии x является окружностью с радиусом r. Таким образом, Fx = * r \ Легко угадать соотношение по сходству треугольников y_x R ~ H *
Смотрите также:
