Оглавление:











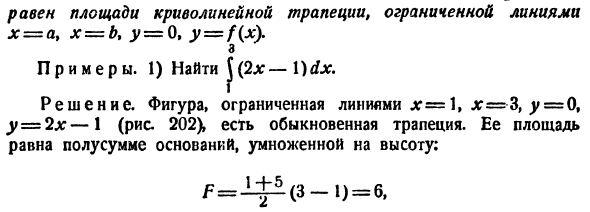







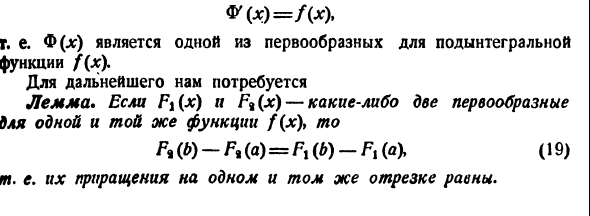

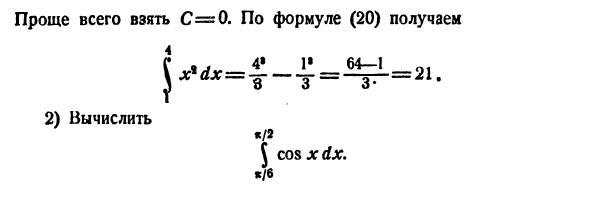



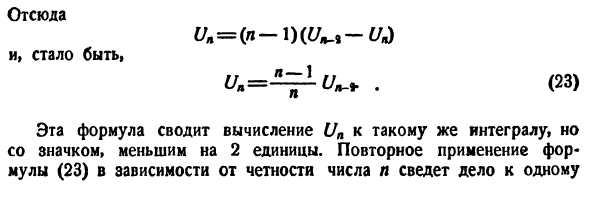

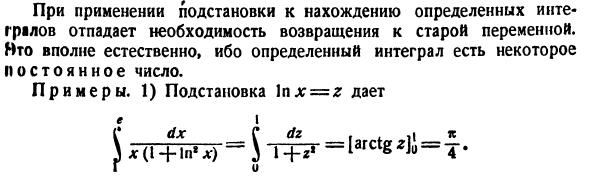



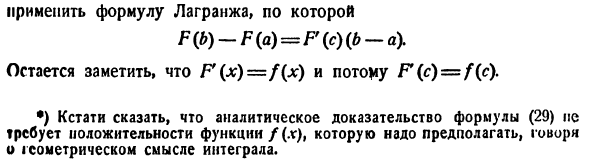

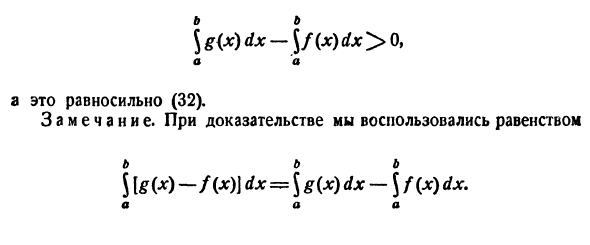



Определение и важнейшие свойства определенного интеграла
Определение определенных интегралов и наиболее важных свойств № 1. Проблема с удочкой Чтобы приблизиться к понятию определенных интегралов, рассмотрим физическую проблему. Глава Я объяснил среднюю плотность и истинную плотность III удилища. Напомним, что средняя плотность стержня — это отношение его массы к длине, а истинная плотность стержня в данной точке — это предел средней плотности бесконечно малой части стержня, которая сжимается до вышеупомянутой точки. пожалуйста. Если стержни одинакового сечения по длине имеют одинаковую массу, такой стержень называется однородным.
- Для такого стержня истинная плотность во всех его точках одинакова и равна его средней плотности *). Если стержень не является однородным, его истинная плотность меняется от точки к точке. Охарактеризуйте положение точки на стержне расстоянием x от одного из концов стержня (и для краткости назовем его точкой x •), и истинная плотность p стержня в точке x зависит от этого x То есть функция х p = p (x \ (1) •) На самом деле масса однородного стержня равна m, а его длина равна /. Затем разделите стержень на сегменты равной длины, по крайней мере, 1000, средняя плотность всего стержня =, по крайней мере, 1000. Для каждого из них в среднем , — = — = /? Равно Средняя плотность / 1 1000 Небольшая часть стержня равна средней плотности всего стержня. В остальном все понятно.
В случае однородного стержня задача решается немедленно. Наверняка для такой удочки Pi *) = P = J, Откуда m = pl (2) Теперь рассмотрим проблему неравномерности удочек. Разбивает ядро (мысленно) на n очень маленьких (не обязательно равных) секций.
Мы поднимаем проблему: узнаем длину стержня I и его истинную плотность (1), рассмотрим ее как непрерывную функцию от xt и найдем массу m стержня. Людмила Фирмаль
Для этого отметьте среднюю точку n-1 на стержне *) x \ •••» li Если вы называете раздел [lgv, первый раздел, второй раздел [jcj, x *] и т. Д., Номер раздела {xk_v xk] будет равен k. Длина этого раздела x <r ° b b ** 4 = ‘ Рисунок 198. Xft-xb_%. Если все разделы маленькие, самый длинный раздел маленький. Его длина или максимальное значение разности xk называется рангом раздавленного стержня и обозначается X. L = максимум (** — JflwX
Непрерывность, эта функция не успевает заметно измениться на «** -!», Если только этот сегмент очень мал, т.е. f (x) является сегментом [xk_i, и эти сегменты малы , Прямоугольник (один из этих прямоугольников заштрихован на рисунке 201). В некоторой точке Xk в этом сегменте возьмите f (x) в качестве общего значения xk_lt (выбор этой точки является приблизительным расчетом Точки сегмента [xk_h xk] равны, поэтому мы получаем прямоугольную высоту, которую мы берем в нашей полосе (XK) F.
Длина основания этого прямоугольника, очевидно, равна Xk − 1, поэтому площадь одной полосы равна произведению f (% k) (xk — следовательно, интересующая область F Изогнутая трапеция почти равна (8) Исходя из самого заключения, точность этого уравнения тем яснее, чем меньше отрезок, т. Е. Чем меньше размер помола X. Тем не менее, точное значение области F является общим пределом в письменной форме, если X-> 0. N F = \ m ^ f (Xk) (xh-lu-i). Рисунок 202.
- Однако, поскольку сумма (8) является суммой Римана, Определение его предела в является интегральным \ f (x) dx. но Итак, мы достигаем формулы (9) F = \ f (x) dx. & Прочитайте это справа налево, мы находим Геометрический смысл интеграции. Когда f (x) является непрерывным и положительным б на [a, b > тогда интеграл J f (jc) dx
Равно площади изогнутой трапеции, окруженной линией x = a, x = b, y = 0, y = f (x). s Пример. 1) Найти || (2x-1) </ l. Решения. Фигура, заключенная в линии jc = 1, dg = 3, y = 0, y = 2x — 1 (рисунок 202), представляет собой нормальную трапецию. Его площадь равна половине суммы оснований, умноженной на высоту. F = ± Neg ^ (3-л) = 6
Откуда 5 (2lg-1) </ lg = 6. 2) Найти \ Vr * -x * dx. ^ о _ Решения. \ (рис. 203) составляет 1/4 от окружности с центром в начале координат и радиусе R. Площадь этой фигуры -i * R \ откуда Теперь, когда мы еще не научились вычислять конкретный интеграл, эти примеры должны были опираться на помощь геометрии.
На линии оси Часть линии, полученная при изменении половины окружности x% + y4 = R \ x от 0 до R, находится под первым координатным углом. Поэтому «рисунок заключен в линию X = 0, x = R, y = 0t y = VR * -x Людмила Фирмаль
В будущем, наоборот, с помощью интегральных вычислений можно вычислить площадь различных форм кривой *). № 4. Два простейших свойства интеграции. Имея дело с неопределенными интегралами, J cos x dx = sin x -f- C, J cos z dz = sin z -f-C, J cos tdt = sin / -f C Таким образом, независимая переменная была обозначена той же буквой в записи подынтегральной функции и записи результата интегрирования. Следовательно, назначение этой независимой переменной, называемой переменной интегрирования, оказалось важным **). Наоборот Рисунок 203.
I. Указание переменной интеграции для конкретной интеграции не играет никакой роли (10) Читатели могут быстро понять это, задавая вопросы. {(2x> + x) dxt $ (2 * »4-f) dt (11) s Больше? Очевидно, то же самое! Если вы заметили, что вам нужно разделить сегмент [3, 5] на более мелкие части для вычисления интеграла (11), выберите точки в каждой части и вычислите значение подынтегральной функции в нем, Я понимаю это более ясно. Интеграл тот же.
Например, комбинация двойного куба аргументов и самого аргумента). Другими словами, все расчеты в обоих случаях одинаковы. Эта ситуация также применима к более общему интегральному случаю (10), который доказал определенную характеристику I определенного интеграла. Передайте это еще одно важное свойство и в выражении \ f (x) dx но Рисунок 204. X Предполагается <b. Что должен понимать символ ] / (х) дх?
На этот вопрос легко ответить, если вспомнить геометрический смысл интеграции. В этом случае стороны изогнутых трапеций x = a и x = b объединяются в одну прямую линию x = a, и трапеция вырождается в прямой сегмент (рис. 204). Поскольку площадь этого сегмента равна нулю, но но (12) Это II. Определенный интеграл с совпадающими пределами интегрирования равен нулю *). Например (S), № 6. Интеграция как функция верхней границы. теорема б Барроу. Предел конкретного интеграла J f (x) dx но Оказывается, что фиксированные и интегральные значения постоянны. Однако, если числовые значения a и b изменяются, интегральное значение также изменяется.
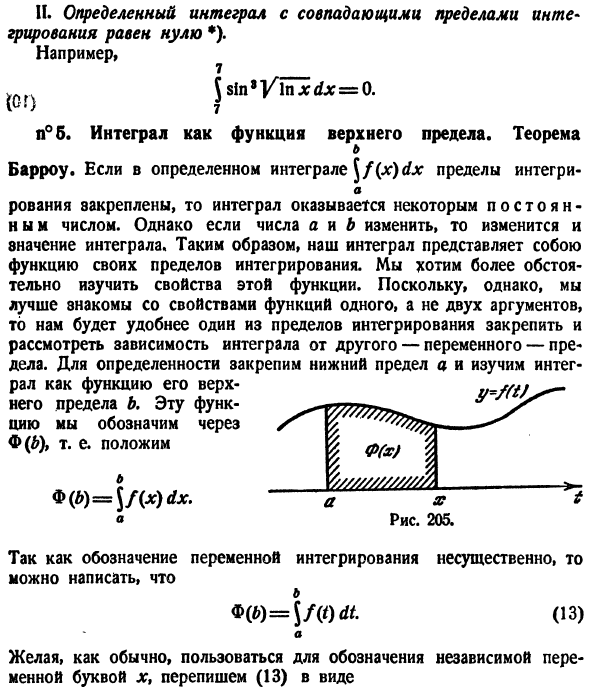
Таким образом, интеграция является функцией пределов интеграции. Я хотел бы изучить свойства этой функции более подробно. Однако, поскольку вы понимаете свойства одной функции лучше, чем два аргумента, удобнее изменить одно из ограничений интеграции и рассмотреть возможность использования другого переменного предела интеграции. Для ясности измените нижнюю границу а и изучите подынтегральное выражение. Ral b как функция верхней границы.
Эта функция представлена Φ (b). Это значит Φ (b) = 1 / (x) dx. х Рисунок 205. Fm faM2 Поскольку указание переменной интеграции не является обязательным, ее можно записать следующим образом. • «- $ /» * (13) о Как обычно, чтобы указать независимую переменную с помощью буквы x, перепишите (13) в следующем виде: Используя функцию (14), мы можем дать уравнение (12) в виде Φ (π) = 0. Предполагая, что f (t) непрерывен и / (/)}> 0). Далее (рис. 205) Φ (x) — площадь фигуры, заключенная в линии t = a> t = x, v = 0, y = fit).
Возможно, наиболее важной теоремой для математического анализа является дифференциальная теорема для функции Φ (x), которая была доказана в 1669 году британским математиком Барроу ). Теорема Барроу. Производная конкретного интеграла как функция верхней границы равна значению подынтегрального выражения в точке производной π. е. Рисунок 206. (15) Доказательство.
Используя геометрический смысл интеграции, на чертеже показан процесс ее дифференциации. Этот процесс должен начинаться с фиксации производной точки x и нахождения соответствующего значения функции Φ (q). Средства, Показано на рисунке. 205. Далее нам нужно указать приращение Ajc в качестве аргумента и найти соответствующее приращение функции LF. Из рисунка видно, что 206 НЧ — это область заштрихованной узкой полосы.
Эта полоса может почти взять За пределами прямоугольника bx и высоты f () (функция f (0) непрерывна, поэтому нет существенного времени для значительных изменений при изменении t между x и jc-f-hell для). DF = / 00 AJC, Откуда AF г / ч
Точность этого приближенного уравнения увеличивается с уменьшением Dx. Таким образом, когда Dat уменьшается, левая часть (16) уравнения приближается к правой части этого уравнения. Это константа (потому что х фиксирован). Вот так Айт-0 ** Однако это означает, что f (x) = W (x) t и доказывает (15).
Попробуйте найти хотя бы приблизительную массу участка Я вышла замуж Для этого функция p (x) существенно не изменяется, поскольку предыдущий раздел мал (непрерывен!). Следовательно, мы можем приблизительно принять, что p (x) постоянна в сечении xk]. Для значения этой константы может быть получено значение p (Xk) произвольно выбранной функции p (x). *) Очевидно, чтобы расширить ядро до n секций, вам нужно только взять n-1 вместо n точек деления. Например, если вы обрезаете бревно до 6, вам нужно сделать только 5 обрезок вместо 6.
Пример, показывающий теорему Барроу, это соотношение (Jjcos11 dtj = cos3 e * y dyj = dy) = e **. Ур Кроме того, 5 {[V ^ tdt} = 0, 2 6 _ Целое число \ ntdt является константой! 2 N ° C. Расчет определенного интеграла. Формула Ньютона — Лейбниц. Ставит проблему вычисления конкретного интеграла l = \ f (x) dx. (17) но но х Если вы заметили l = \ f (t) dt9 И введите функцию <b (x) = \ f {i) dt.
Тогда вы можете написать / 1 = Φ (б) Или то же самое / = Φ (ξ) -Φ (a), (18) Для φ (α) = $ / (0Λ = a но Следовательно, интеграл / равен приращению функции Φ (x) на интервале [a, b]. Кроме того, согласно теореме Барроу,φ ‘() = / (). То есть Φ (x) является одной из обратных производных подынтегрального выражения f (x ) Что тебе нужно больше Лемма. Если fj (jc), то F% (x) — это две обратные производные одной и той же функции f (x), B (*) — F * (a) = Fx (b) -Fi (a% (19) То есть приращение в том же сегменте равно.
Фактически, две обратные производные одной и той же функции могут отличаться только постоянным членом. смысл Ft (x) = Ft (x) + C Отсюда Ft (b) = Ft (b) 4 C, F, (a) = F, (a) + C Вычитание второго уравнения из первого уравнения дает (19). Теперь предположим, что мы смогли найти обратную производную F (x) функции f (x), используя метод неопределенного интеграла. Поскольку Φ (x) является примитивом функции f (x), лемма От Φ к _Φ (a) = F (b) -F (a). Сравните это с (17) и (18), чтобы найти основную формулу Ньютона-Лейбница. (20) Было установлено, Правила.
Чтобы вычислить конкретный интеграл функции, вам нужно найти обратную производную этой функции и построить разницу между значениями обратной производной в верхнем и нижнем пределах интеграла. Из леммы ясно, что антипроизводная, используемая в уравнении (20), не является проблемой. Пример. 1) Рассчитать 4 [Ххх. Следуйте правилам, чтобы найти x * примитивы. У них есть бесконечное число, и все они объединены выражением $ Самый простой способ — взять C = 0. 4 ххх = 2) Рассчитать Из уравнения (20) 4 «! • 64—1 Q1 «/ 2 J cos xdx. «/ 6
с того времени J cos x dx = sin x + C, Тогда вы можете положить 7 (JC) = SINX. Тогда найдите * / 2 из (20) \ cos x dx = sin y-sin- ^ = 1-y = y К / 6 Разница между символами [F (x)] a и F (b) -F {a) делает запись более экономичной благодаря использованию часто используемых обозначений. Этот символ может использоваться, чтобы дать форму уравнения (20) Или *) (особенно выразительно!) (21)
Например «/ S 2 кг 3 Точно так же, Интеграция частей и подстановка переменных в конкретные интеграции. Все методы, которые могут вычислять неопределенные интегралы, также применимы к определенным интегралам. В частности, чтобы найти последнее, вы можете либо частично интегрировать, либо заменить переменные. При применении этих двух методов к конкретным интеграциям, есть несколько характеристик.
Во-первых, формула интеграции для каждой части конкретной интеграции может быть записана в виде: (22) Фактически, основываясь на (21) и интегральной формуле неопределенной интегральной части, б J и DV = и = [ни-ду ^ а. но Обратите внимание, что письменное выражение соответствует правой части (22). Пример. Ну хорошо 1) J x cos xdx = ^ xd (sm jc) = [jc sin x]% — J sinx (/ A: = 0 0 0 = [cos x] l = −2. 2) Пусть » 2 Un = \ cos «xdx. Тогда один f * _ ~ 2 * 2 Un = ^ cos * ‘1 x d (sin jc) = [sin x cos * 1 «1 x] qЗ \ пхЦаЛ ** х). Первый член справа равен нулю. смысл Jt w_ 2 2 un = (n-1) $ sin’x cosnui-1) 5 (1-COS1 x) cos * -xx dx.
Поэтому, следовательно, , (23) Эта формула уменьшает вычисление Un до того же интеграла, но значок на 2 единицы меньше. Повторное применение уравнения (23) в соответствии с четностью числа n сводит проблему к единице.
Два простых интеграла: = \ cosxdx = \, UQ = \ dx ~ Например ij f, r 6 ,, 6 4 .. 6 4 2 .. 16 cos1 xdx ^ = un = -j (/ B = y’5 • fi = y “y • y = Правило замены задается следующей формулой для конкретной интеграции: б? (&) Что? (O) Отличие от неопределенного интеграла coctqht состоит в том, что при выполнении подстановки полученный интеграл должен установить новую переменную z limit. Для доказательства уравнения (24) левая и правая части представлены Λ и / 7 соответственно. \ f (z) dz = F (t) + C Далее по уравнению Ньютона-Лейбница n = [F (z)] J g Sf [f (”)] _ F [T (a) J. (25) С другой стороны, применяются к неопределенной (I) интеграции $ / M )] ) (e) l (26) Сравнение (25) и (26) дает (24). % 2 секунды (24)
Если вы применяете подстановку, чтобы найти конкретный интеграл, вам не нужно возвращаться к старой переменной. Это очень естественно. Потому что определенный интеграл — это конкретная константа. Пример. 1) Подстановка Inx = z е я J X (1 + L’X) = $ T $? «= Larctg *] J = |.
(Потому что они все почти равны) Раздел 1_egA_1e xb \ Point Xk *). Следовательно, [рис. 198] произвольно принимает [xk_it xk \ point xk, и для каждой точки x из [xk_i agl] p (x) = p (Xk \ xk_it xk \ density p (Xk) однородно Масса этого сечения может быть рассчитана по уравнению (2), и вы можете видеть, что он равен. p (Xk) (xk-xk.,). (3) Масса m всего стержня равна сумме масс k = 1, 2, n (3). Если операция сложения представлена символом 2 **, получается следующая формула. N m = ^ P (Xk) {xk-xk_). (4) 1 Однако письменная эквивалентность не является точной, поскольку предположение об однородности отдельных участков является приближенным.
Если вы замените знак равенства в (4) приближенным знаком равенства, L тд *% р (хк) (хк- (5) Вывод уравнения (5) показывает, что это уравнение является более точным и что чем меньше отдельные участки, тем меньше ранг шлифования k. Следовательно, точное значение массы m не является суммой, которая появляется в (5), но X стремится к нулю N m = lim <p (xl) (xk-xk_ \
2) дать замену x = Rs ‘\ nt *) хорошо R 2 7 \ VR * -хЧх = [R9 cos8 tdt = J (I + cos 2 () dt = Ах ах ах , sin2 £ «] T * /? = ТП 2 Джо № 8. Важнейшая характеристика интеграции. Определение интеграла \ f (x) dx но Мы думали, что нижний предел а был меньше, чем верхний предел б. Затем я добавил отношения \ nx) dx = 0. но Если нижний предел больше верхнего предела, полезно рассмотреть возможность интеграции.
Другими словами, официальная правая сторона Ньютона — Лейбниц б J / C *) dx = F (b) -F (a) (27) но Измените anac при сортировке чисел a и b. Разумно поставить a> b (по определению) \ f (x) dx = — \ f (x) dx, Вот так I. Изменение пределов интеграции изменит знак четкой интеграции. Теперь становится ясно, что уравнение (27) верно во всех случаях a b. Отныне, если нижний предел интегрирования меньше верхнего предела, порядок пределов интегрирования называется нормальным. Следующее важное свойство интеграла, называемого аддитивностью: •) Напомним, что в n’3 я нашел рассматриваемый интеграл на основе геометрического значения. \
II. Если интервал интегрирования [a, b] делится на части точкой c (a <c <b), интеграл по всему интервалу равен сумме интегралов этой части. Это значит J / C *) dx = \ f (x) dx + 5 fix) dx. Поскольку площадь фигуры aABB (рис. 207) равна сумме площадей фигуры aACc и cBBB, эта характеристика явно следует из геометрического смысла интегрирования. Отметим, что уравнение (29) справедливо не только для a <c <b, но также для любого расположения точек a, b и c. На самом деле, если F (x) является примитивной функцией (20) fitX), то формула Ньютона-Лейбница \ f (x) dx = F (c) -F (a), но $ / (■ *) dx = F (b) -F (c). P X и Рисунок 207.
Следовательно, правая часть (29) равна разности Fib) -F (a), которая также равна его левой стороне *). III. Теорема о среднем значении. Существует точка c между a и b следующим образом. (30) Обязательно притяните обратную производную F (x) еще раз и справа от равенства \ f (x) dx = F (b) -F (a)
Применить формулу Лагранжа F (b) -F (a) = F (c) (b-a). Обратите внимание, что F (x) = f (x) и, следовательно, F * (c) = f (c). •) Кстати, аналитическое доказательство уравнения (29) не требует положительной функции / (x), которую следует принимать, когда речь идет о геометрическом значении интегрирования.
Уравнение (30) имеет простой геометрический смысл. Показывает, что изогнутая трапеция aABB (рис. 208) равна прямоугольнику aPQb. Эта прямоугольная высота f (c) называется средней ординатой трапеции aABB. Внутривенно В нормальном порядке пределов интегрирования интеграл положительной функции является положительным числом. Фактически, если a 0, оба фактора справа от уравнения (30) положительны.
Теперь рассмотрим две функции f (x) и g (x) t, определенные в [a, b] (предполагая, таким образом, a <b). если FW <г (А (30 тогда \ f (x) dx <\ g (x) dx, (32) Тем не менее, Это V. В обычном порядке интеграционных ограничений неравенство может быть интегрировано. конечно \ g (x) dx- \ f (x) dx = \ [gW- / (*)] dx. а В последнем интегрировании подынтегральное выражение является положительным (благодаря [31]) и, следовательно, также является положительным. смысл г /\ g (x) dx- \ f (x) dx> 0, а Это эквивалентно (32). Замечания. Мы использовали равенство в доказательстве б б \ g (x) -f (x) \ dx = \ g (x) dx- \ f (x) dx а
С равенством $ 1 / W + £ (*)] dx = \ f (x) dx + \ g (x) dx. \ kf (x) dx = k \ f (x) dx а Это прямой результат выражения б (33) \ f (x) dx = [\ f (x) dx \ Так называемый VI может быть легко выведен из уравнения (30). Оценка интеграла. хорошо ] f (x) dx Фактически, абсолютное значение произведения f (c) (b-a) не превышает значение справа от (33). Пример. Поскольку | sinjc | ^ l, для x> 10 sinx I cr — 10 ~ так 16 <6,10-е <10 «л грех х \ + х IDX (34) Этот пример показывает практическое значение неравенства (33). Представьте себе, что расчет конкретной конструкции, такой как мост, приводит к тому, что нагрузка, связанная с конкретным узлом в этой структуре, выражается в интегралах (в тоннах).
грех Х \ + х * s дх. (35) Письменный интегральный расчет очень сложен. Однако неравенство (34) показывает, что интересующий груз составляет менее 10-7 тонн или менее 0,1 грамма! Ясно, что вычисление интеграла (35) не имеет смысла, но его просто следует игнорировать.
Мы можем видеть, что наша физическая проблема привела к особой форме ограничения (6). Позже вы обнаружите, что многие конкретные решения проблем приводят к таким ограничениям. Поэтому при изучении этих пределов возникла чисто математическая проблема.
Каждый такой предел называется определенным интегралом. В следующем разделе дается точное определение этой концепции. *) Символ k в обозначении точки указывает, что область выбрана из числа k. • *) Это греческая прописная буква .sigma *. Строчная .cmma * выглядит так:№ 2. Определенный интеграл. Предположим, что функция f (x) задана в интервале b].
Выполните следующие пять операций над сегментом | a, b \ и функцией f (x): 1. Используйте точку JTf, x где Λ = 1, 2, …, л, X. Эта величина, которая характеризует, насколько хорошо сегментирована [a, b] t, называется рангом выполненной фрагментации. 2. Для каждого сегмента выберите точку Xk> xk_t ^ ^ Xk ^ xk и вычислите значение f (Xk) функции f (x) в этой точке. 3. Умножьте f (Xk) на длину сегмента xk-xk_x [xk_v xk . 4. Суммируйте все полученные продукты. То есть подвести итог. N
1 Эта сумма называется интегральной суммой или суммой Римана (после немецкого математика 19-го века, который изучал такие суммы). 5. Раздавить полученный измельченный материал до нуля А. Во многих случаях это улучшение делает сумму Римана конечным пределом *) /. Это не зависит от способа выбора точки разделения xk или способа выбора промежуточной точки Xk. Этот предел / = Lim O X-O L Вызывается определенный интеграл функции f (x) по интервалу [a, b .
б \ f (x) dx. Числа a и b называются нижним и верхним пределами интегрирования соответственно, а интервал [a, b] называется интервалом интегрирования. Вот так •) Так, например, ситуация n’l, а сумма с является приблизительным значением массы стержня, чем выше точность, тем меньше ранг дробления.
Определенный интеграл является конечным пределом суммы Римана, когда ранг фрагментации, производящий эту сумму, стремится к нулю *): б н \ f (x) ix = Um £ / (> ( но Не все функции имеют определенные интегралы, потому что определенные интегралы являются пределами определенной переменной, а не всех переменных. Но важно Если функция теоремы f (x) непрерывна в интервале [a, b \ б \ f (x) dx но Exist.
Эта теорема принимает без доказательства. Далее рассматриваются в основном непрерывные функции, но более общие функции о Теорема * Если f (x) кусочно, существует интеграл \ f (x) dx но Непрерывный \ Понятие кусочно-непрерывной * функции легко объяснить на простом примере. Дайте функцию fx (x), чтобы сделать ее непрерывной [Функция f% (x) функции c, b \ прерывиста с [a, c \ a. Функция f (x \ соответствует f ^ (x) a ^ x <jc и f% (x) c <^. X <, b (это равно / (c) и не важно ) Состоит из двух последовательных частей * (рис. 199): такая функция называется кусочно-непрерывной.
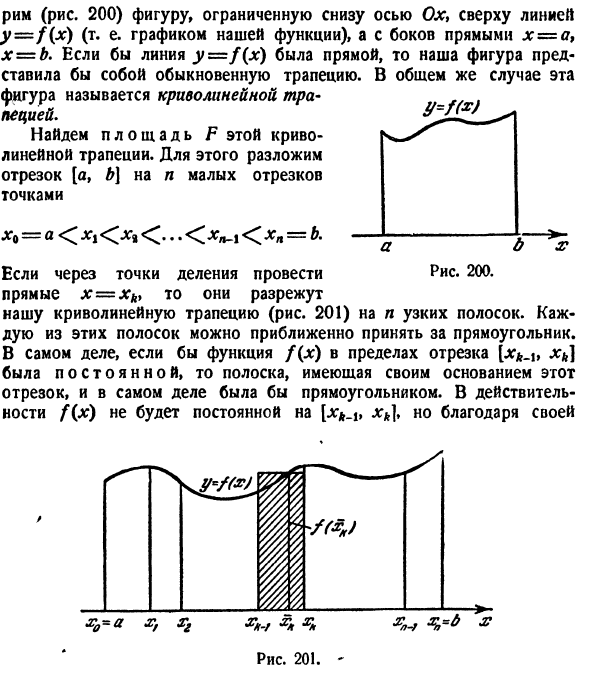
Непрерывная часть. Тем не менее, если не указано иное, подынтегральное выражение предполагается непрерывным. n ° C Интегральное геометрическое значение / f (x) является положительной непрерывной функцией, определенной в интервале [a, b]. •) Обратите внимание, что дробление, то есть набор точек разделения g *, не полностью определяет общее значение a. Для работы необходимо указать дополнительную середину Рассмотрим диаграмму с осью Ox снизу, прямой линией y = zf (x) сверху (то есть графиком функций) и прямой линией x = a9 x = b со стороны (рис. 200). Если линия y = f (x) — прямая, фигура будет нормальной трапецией. В общем случае эта фигура называется изогнутой трапецией. Найдите область F этой изогнутой трапеции.
Для этого разложите сегмент [a, b \ на n небольших сегментов в точках d0 = a << x% <… <* 1 <= b. Если прямая линия x = xh> проходит через точку деления, разрежьте изогнутую трапецию (рис. 201) на n узких полос. Каждую из этих полос можно считать примерно прямоугольной. Фактически, если функция f (x) является постоянной в интервале [xk_ \ t jt *], полоса, основанная на этом сегменте, фактически является прямоугольником. На самом деле, f (x) не является постоянной величиной, Рисунок 200
Смотрите также:
