Оглавление:
Теорема Коши. Первообразная и неопределенный интеграл. Формула Ньютона-Лейбница
Теорема 75.1 (Коши). Если функция  аналитична в односвязной области
аналитична в односвязной области  , то интеграл от этой функции по любому замкнутому контуру
, то интеграл от этой функции по любому замкнутому контуру  , лежащему в области
, лежащему в области  равен нулю, т. е.
равен нулю, т. е. 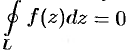 .
.
Докажем теорему, предполагая непрерывность производной 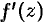 (это упрощает доказательство). По формуле (75.2) имеем:
(это упрощает доказательство). По формуле (75.2) имеем:
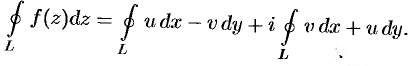
В силу аналитичности 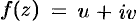 и непрерывности
и непрерывности 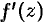 в односвязной области
в односвязной области  , функции
, функции 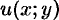 и
и 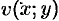 непрерывны и дифференцируемы в этой области и удовлетворяют условиям Эйлера-Даламбера:
непрерывны и дифференцируемы в этой области и удовлетворяют условиям Эйлера-Даламбера: 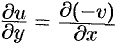 и
и 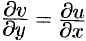 . Эти условия означают равенство нулю интегралов
. Эти условия означают равенство нулю интегралов 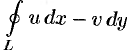 и
и 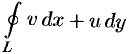 (см. теорему 56.3). Следовательно,
(см. теорему 56.3). Следовательно, 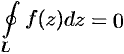 .
.
Теорема Коши допускает распространение на случай многосвязной области.
Рассмотрим для определенности трехсвязную область  , ограниченную внешним контуром
, ограниченную внешним контуром  и внутренними контурами
и внутренними контурами 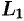 и
и 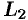 . Выберем положительное направление обхода контуров: при обходе область
. Выберем положительное направление обхода контуров: при обходе область  остается слева (см. рис. 289).
остается слева (см. рис. 289).
Пусть функция  аналитична в области
аналитична в области  и на контурах
и на контурах  ,
, 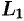 и
и 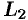 (т. е. в замкнутой области
(т. е. в замкнутой области 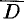 ; функция называется аналитической в замкнутой области
; функция называется аналитической в замкнутой области 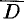 , если она аналитична в некоторой области, содержащей внутри себя область
, если она аналитична в некоторой области, содержащей внутри себя область  и ее границу
и ее границу  ).
).
Проведя два разреза (две дуги) 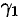 и
и 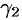 области
области  (см. рис. 289), получим новую односвязную область
(см. рис. 289), получим новую односвязную область 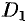 , ограниченную замкнутым ориентированным контуром
, ограниченную замкнутым ориентированным контуром 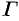 , состоящим из контуров
, состоящим из контуров  ,
, 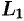 ,
, 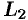 и разрезов
и разрезов 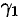 и
и 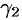 :
: 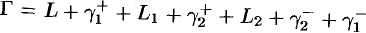 . По теореме Коши для односвязной области
. По теореме Коши для односвязной области 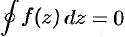 , но
, но
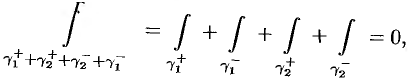
т. к. каждый из разрезов (дуг) 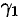 и
и 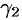 при интегрировании проходится дважды в противоположных направлениях. Поэтому получаем:
при интегрировании проходится дважды в противоположных направлениях. Поэтому получаем:
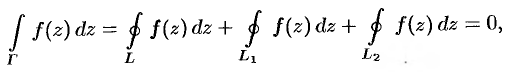
т.e. интеграл от аналитической в замкнутой многосвязной области 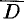 функции
функции  по границе области
по границе области  , проходимой в положительном направлении, равен нулю.
, проходимой в положительном направлении, равен нулю.
Замечание. Изменив направление обхода внутренних контуров 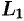 и
и 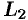 , будем иметь
, будем иметь 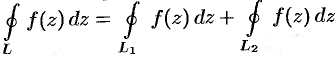 , где все контуры (
, где все контуры ( ,
, 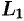 и
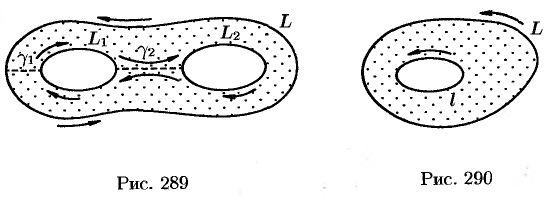
и 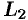 ) обходятся в одном направлении: против часовой стрелки (или по часовой стрелке). В частности, если
) обходятся в одном направлении: против часовой стрелки (или по часовой стрелке). В частности, если  аналитична в двусвязной области, ограниченной контурами
аналитична в двусвязной области, ограниченной контурами  и
и 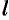 и на самих этих контурах (см. рис. 290), то
и на самих этих контурах (см. рис. 290), то 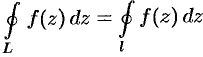 , т. e. «интеграл от функции
, т. e. «интеграл от функции  по внешнему контуру
по внешнему контуру  равен интегралу от функции
равен интегралу от функции  по внутреннему контуру
по внутреннему контуру 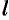 » (контуры
» (контуры  и
и 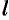 обходят в одном направлении).
обходят в одном направлении).
Следствие 75.1. Если  — аналитическая функция в односвязной области
— аналитическая функция в односвязной области  , то интеграл от нее не зависит от формы пути интегрирования, а зависит лишь от начальной точки
, то интеграл от нее не зависит от формы пути интегрирования, а зависит лишь от начальной точки 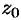 и конечной точки
и конечной точки  пути интегрирования.
пути интегрирования.
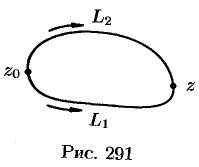
Действительно, пусть 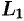 и
и 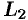 — две кривые в области
— две кривые в области  , соединяющие точки
, соединяющие точки 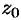 и
и  (рис. 291).
(рис. 291).
По теореме Коши 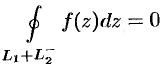 , т. е.
, т. е. 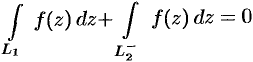 , или
, или 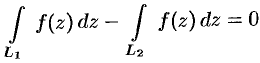 , откуда
, откуда 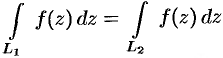 .
.
В таких случаях, когда интеграл зависит только от начальной точки и конечной точки пути интегрирования, пользуются обозначением 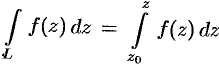 . Если здесь зафиксировать точку
. Если здесь зафиксировать точку 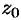 , а точку
, а точку  изменять, то
изменять, то 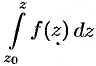 будет функцией от
будет функцией от  . Обозначим эту функцию через
. Обозначим эту функцию через 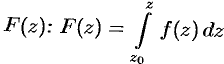 . Можно доказать, что если функция
. Можно доказать, что если функция  аналитична в односвязной области
аналитична в односвязной области  , то функция
, то функция 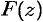 также аналитична в
также аналитична в  , причем
, причем
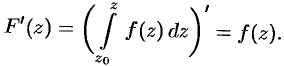
Функция 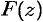 называется первообразной для функции
называется первообразной для функции  в области
в области  , если
, если 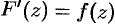 .
.
Можно показать, что если 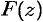 есть некоторая первообразная для
есть некоторая первообразная для  , то совокупность всех первообразных
, то совокупность всех первообразных  определяется формулой
определяется формулой 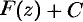 , где
, где 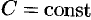 .
.
Совокупность всех первообразных функций  называется неопределенным интегралом от функции
называется неопределенным интегралом от функции  и обозначается символом
и обозначается символом 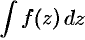 , т. е.
, т. е.
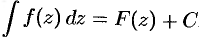 , где
, где 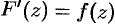 .
.
Пусть функция 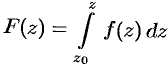 есть первообразная функция для
есть первообразная функция для  . Следовательно,
. Следовательно, 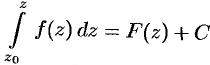 . Положив здесь
. Положив здесь 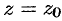 , получим
, получим 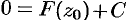 (контур замкнется, интеграл равен нулю). Отсюда
(контур замкнется, интеграл равен нулю). Отсюда 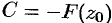 , а значит,
, а значит,
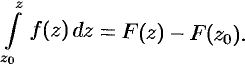
Полученная формула называется формулой Ньютона Лейбница.
Интегралы от элементарных функций комплексного переменного в области их аналитичности вычисляются с помощью тех же формул и методов, что и в действительном анализе.
Так, 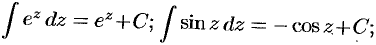
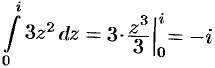 и т.д.
и т.д.
Пример №75.2.
Вычислить интегралы: 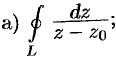
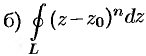
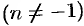 , где
, где  есть окружность радиуса
есть окружность радиуса 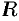 с центром в точке
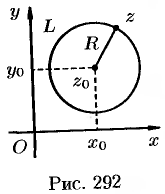
с центром в точке 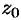 , обходимая против часовой стрелки (см. рис. 292).
, обходимая против часовой стрелки (см. рис. 292).
Решение:
а) Теорема Коши неприменима, т.к. функция 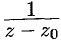 не аналитична в точке
не аналитична в точке 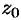 . Параметрические уравнения окружности
. Параметрические уравнения окружности  есть
есть 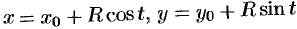 , где
, где 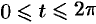 . Следовательно,
. Следовательно,
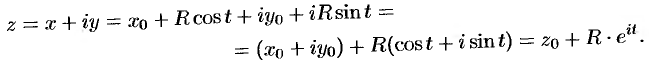
Таким образом, мы получили, что комплексно-параметрическое уравнение данной окружности есть 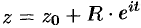 ,
, 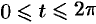 . Поэтому по формуле (75.4) получим:
. Поэтому по формуле (75.4) получим:
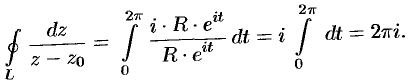
б) При 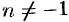 имеем:
имеем:
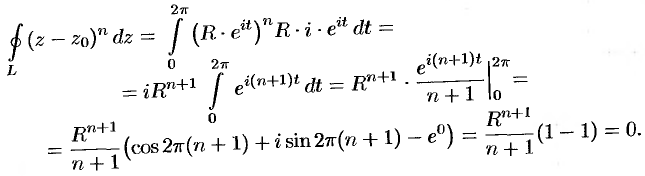
Итак,
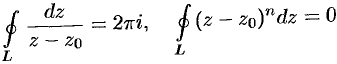 ,
,  — целое,
— целое, 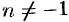 .
.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Геометрический смысл модуля и аргумента производной |
| Интегрирование функции комплексного переменного |
| Интеграл Коши. Интегральная формула Коши |
| Нули аналитической функции |
