Оглавление:





Исследование нелинейных колебаний на фазовой плоскости. Основные определения
- Среди различных методов исследования нелинейных колебаний одним из наиболее распространенных и описанных является представление движения в фазовой плоскости или в фазовом пространстве. Этот метод позволяет ответить на наиболее важные вопросы, характеризующие движение системы без интегрирования дифференциальных уравнений движения. Это важно, поскольку во многих случаях нелинейные дифференциальные уравнения не могут быть интегрированы в замкнутом виде. Представление движения на фазовой плоскости позволяет найти возможные равновесные состояния и определить устойчивость равновесия системы.
Используя структуру на фазовой плоскости, можно найти периодическое движение системы и исследовать переходные процессы к состоянию устойчивого движения в зависимости от различных параметров и начальных условий движения. Когда нелинейные дифференциальные уравнения могут быть интегрированы в замкнутом виде, выражение движения на фазовой плоскости позволяет ответить на вопросы о возможном равновесном состоянии и устойчивости движения системы, а также установить влияние различных параметров и начальных условий движения на устойчивость этих состояний. Мы быстрее изучили изменение материальных точек и построили отклонение точек от равновесных положений в зависимости от времени.
Общее решение этого дифференциального уравнения равно сумме общего решения соответствующего однородного уравнения и частного решения уравнения (1), т. Людмила Фирмаль
Если такие графики получены экспериментально путем регистрации отклонений, измеренных в специальном приборе, то они называются осциллограммами. Эти графики позволяют определить местоположение точки или системы в любой момент времени, но не знают зависимости скорости от координат. Рассмотрим положения, лежащие в основе исследования движения системы с использованием фазовой плоскости.
Дифференциальное уравнение для нелинейного колебательного движения системы с 1 степенью свободы может быть записано в виде — X X, D 0, 1 Где x, D x-обобщенные координаты системы, а также 1-я и 2-я производные по времени, где -циклическая частота системы, — время, — нелинейная функция аргументов, указанных в скобках. Если функция явно зависит от времени, то система называется неавтономной. Если функция явно не включает время, то система называется автономной. Маркировки Уравнение 2 может быть представлено в виде системы, состоящей из двух уравнений 1-го порядка. .Х, Y, 1 -k2x О.
Ограничившись рассмотрением автономных систем в этом пункте, напишите систему 2 в следующей форме 3 Плоскость переменной xi y xD где x и y-ортогональные декартовы координаты называется фазовой плоскостью. Если координаты x и скорость y известны в какой-то момент времени, Предположим, что состояние нелинейной системы определено. Тогда каждая точка на фазовой плоскости соответствует единственное состояние системы. Так, на фазовой плоскости называется фазовой плоскости, а точка на фазовой плоскости называется точкой изображения По мере изменения состояния системы точки изображения перемещаются вдоль фазовой плоскости.
Локус, описываемый точкой изображения, называется фазовым локусом. Если система движется периодически, то фазовая траектория становится замкнутой кривой. Начало фазовой плоскости x 0 и y 0 — это положение равновесия. Изменяя начальные условия движения, можно получить набор фазовых траекторий, удовлетворяющих фазовой плоскости. Этот набор фазовых локусов называется фазовым портретом системы и может ответить на многие вопросы о характере движения системы. Дифференциальное уравнение для фазового локуса найдено из 3. ау ПП х-г Интегральная кривая, соответствующая уравнению 4, в простейшем случае является фазой locus. In в более сложных случаях она соответствует нескольким фазам траектории.
Уравнение фазового локуса определяет зависимость координат от скорости движения исходной механической системы. Скорость точек изображения на фазовой плоскости называется фазовой скоростью. Модуль фазовой скорости В Уш Ш 5 Важным в изучении движения системы является ее равновесие state. At при этом скорость 6×161 y и ускорение 6y Когда 61 P x, y исчезает, система находится в равновесии. Если сравнить эти условия с модулем уравнения фазовой скорости 5, то следует отметить, что в равновесном состоянии системы фазовая скорость равна нулю. 1. через каждую точку фазовой плоскости проходят две фазовые траектории. Исключением является точка равновесия, которая называется singularity.
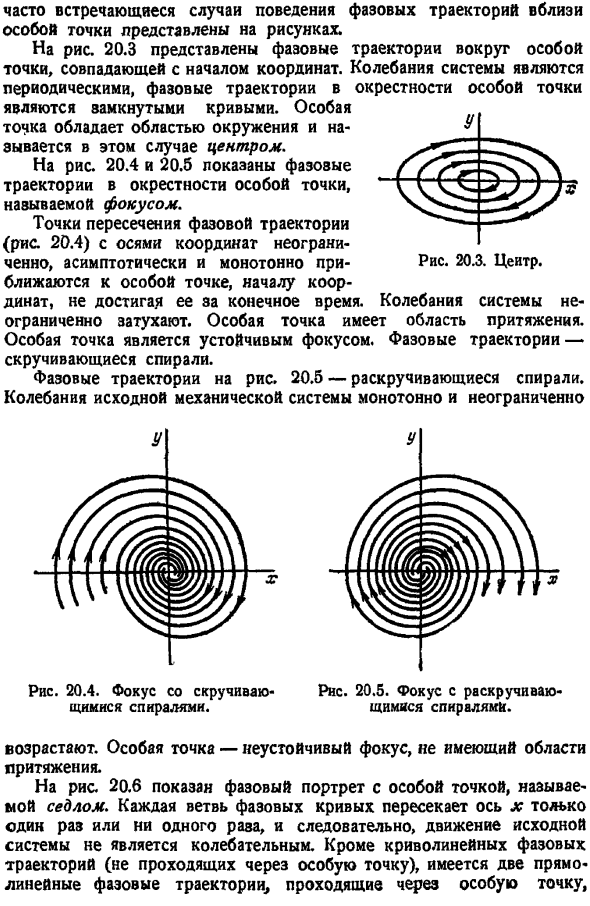
- В этих точках касательность фазового локуса неопределима, так как и числитель, и знаменатель уравнения 4 исчезают одновременно. Таким образом, нарушается одно из условий теоремы Коши о единственности решения дифференциального уравнения 4.Все точки фазовой плоскости, за исключением специальных, называются обычными. Работа фазового локуса вблизи сингулярности зависит от параметров системы и начальных условий движения. Наиболее распространенный случай работы фазового локуса вблизи сингулярности показан на рисунке На рис. 20.3 показаны фазовые траектории вокруг сингулярности, совпадающие с началом координат. Вибрация системы периодична фазовый локус вблизи сингулярности Замкнутая кривая.
Сингулярность имеет окружение, в этом случае она называется центром. На рисунках 20.4 и 20.5 показаны фазовые траектории вблизи сингулярности, называемой фокусом. Пересечение фазовых траекторий рис. 20.4 и осей координат является неограниченным, асимптотическим и монотонным. Приближаясь к сингулярности, началу координат, не достигая конечного времени. Система колеблется бесконечно затухая. Некоторые точки имеют зону притяжения. Сингулярность-это устойчивый фокус.
При этом значения угла поворота и угловой скорости диска в моменты, когда данное дифференциальное уравнение утрачивает силу, оказываются начальными условиями для последующего дифференциального уравнения. Людмила Фирмаль
Фазовая траектория. Не скручено. Фазовые траектории на рисунке 20.5-раскручивание спирали. Колебания ранних механических систем монотонны и необузданны Рис. 20.4.Поверните спираль, чтобы сосредоточиться. Рис. 20.5.Сосредоточьтесь на вращающейся спирали. Он будет увеличиваться. Особой точкой является неустойчивый фокус, который не имеет зоны притяжения. На рисунке 20.6 показан фазовый портрет с сингулярностью, называемой седлом. Каждая ветвь фазовой кривой пересекает ось x на 1 или не пересекает ни одной области, поэтому движение исходной системы не происходит oscillate.
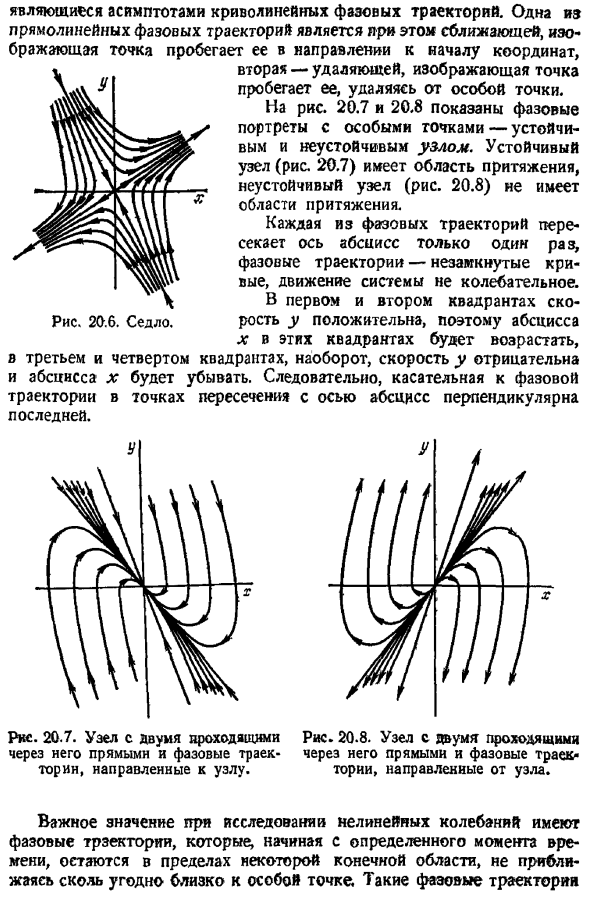
Кроме криволинейного фазового локуса который не проходит через сингулярность, есть 2 линейных фазовых локуса, которые проходят через сингулярность. Это асимптоты фазы кривой locus. In в этом случае 1 из линейных фазовых траекторий приближается, точка рисования бежит к началу координат,2-я удаляется, а точка рисования удаляется от сингулярности и проходит через нее. На рис. 20.7 и 20.8 показан фазовый портрет с сингулярностями-устойчивыми и неустойчивыми узлами. Узел стабильности рис.20.7 имеет привлекательную область, а неустойчивый узел рис. 20.8 не имеет привлекательной области.
Каждая фазовая орбита пересекает горизонтальную ось в 1 раз, фазовая орбита представляет собой открытую кривую, и движение системы не колеблется. В 1-м и 2-м квадрантах скорость y положительна, поэтому абсцисса x этих квадрантов увеличивается. Напротив, в 3-м и 4-м квадрантах скорость y отрицательна, а абсцисса x равна reduced. So, касательная фазового локуса на пересечении с осью абсцисс перпендикулярна оси абсцисс. Рис. 20.7. Узел, через который проходят 2 прямые линии, и фазовый локус, направленный к узлу. Рис. 20.8. Узлы, через которые проходят 2 прямые линии, и фазовые траектории от узлов.
При изучении нелинейных колебаний важен фазовый локус, который начинается в определенный момент и остается в определенной конечной области, не приближаясь произвольно к определенной точке. Такой фазовый локус пересекает абсциссу и бесчисленное множество. Возможными формами такого фазового локуса являются спираль и замкнутая кривая. Замкнутая кривая в этом случае называется предельным циклом.
Если спираль закручена, то предельный цикл находится внутри спирали, а если спираль не закручена, то она находится снаружи. Предельный цикл становится стабильным и неустойчивым рис. 20л. На этом рисунке показаны 2 предельных цикла. Большой радиус-стабильный-малый радиус-нестабильный. Устойчивый предельный цикл характеризуется тем, что при небольшом начальном отклонении от него точка изображения приближается к предельному циклу асимптотически по спирали.
Устойчивый предельный цикл соответствует автоколебаниям системы. Если предельный цикл нестабилен, то небольшое отклонение от него приведет к появлению изображения Живая точка удаляется от предела. 20.9. Цикл, который. В следующем абзаце приведен пример построения фазового портрета линейной системы с 1 степенью свободы. Sec. At 3, построен фазовый портрет нелинейной системы с 1 степенью свободы. Среди множества приближенных методов построения фазовых траекторий метод изокрайнера, метод Дробова, метод Ренара, метод Пелла и др.
Смотрите также:
Предмет теоретическая механика
| Свободные нелинейные колебания | Фазовые портреты линейных систем |
| Вынужденные нелинейные колебания | Дельта-метод |
