Оглавление:




Исследование поведения сжатого стержня при потере устойчивости за пределом упругости
- Исследование поведения сжатого стержня при потере устойчивости за пределом упругости. Более подробно прослеживается поведение компрессионного стержня с увеличением силы сжатия. Мы рассматриваем этот материал как следующую фигуру уплотнения с линейным упрочнением(рис. 217). Приращения напряжений
и деформаций при нагрузке и разгрузке связаны соотношениями (139.2) и (139.3) соответственно, а в Формуле (139.2) тангенсный коэффициент Et постоянен. Укорочение оси стержня после разветвления, то есть при изменении нагрузки от Po до P, указывает на то, что она проходит через соответствующую кривизну кривой оси x-стержня. Деформация волокон с координатой y,
возникающая после разветвления, обозначается знаком De. Очевидно, что De=D e — / — Людмила Фирмаль
x y — (141.1) рис. Двести семнадцать При нейтральной оси De = 0 эта ось отстает от оси x на расстояние y0== — De/X. Если вы добавите(141.1)и(139.2)и(139.3), вы получаете: о=£т (а Е4-ху), у>У0,К=£(Д х г), г<У0. В дальнейшем рассмотрим поперечное сечение стержня d r=R-Ro с высотой 2 L и шириной B и рассчитаем изгибающий момент W: 4-A L Uo b. P=b B o d y=. Т Дж(Д Е-| — ху) Д Г — \ — Е^(Е-[- X Г) Д Г= — Л У0-ч =У N»(Л Е-Х Л Г+? (Д Е+Х Л) ’ } ’ ( 1 4 1 −2 >
ч ч ч н М=б J н о г ды=ставка^(е-\ — х г) г г г — \ — е (и Е — \ — ху) м г= -ч г-ч. =■(ХL-де)’(2XL с ае) 4″»е (ХL де)’ (сегодня 2XL-де) ’ (141.3) в правой части уравнения (141.2) и (141.3) представляет собой первый-степень однородной функции по отношению к де и X. ХІІ (141.4) * _ * Уравнения (141.2) и (141.3) принимают следующий вид:•(ex)»|1 (ex)»==4x,^=-7^[(x -«), (2x4-e) 4-|(x+e) (2x-e)]. Если исключить еиз
- системы уравнений (141.4), то получим нелинейную зависимость между изгибающим моментом и кривизной. Соответствующий расчет слишком сложен, поэтому достаточно выяснить характер полученной зависимости. Прежде всего, следует отметить, что соотношение (141.4) справедливо только в том случае, если|y0-L, то есть в разрезе имеется зона погрузки и разгрузки. Если вы вспомните формулу для U0, вы увидите, что HL De поэтому должен иметь x>e. — За всю Х<^есекция нагрузки, Л Л=^Х-^ Если вы проходите в безразмерной величине, вы получаете t — I(x<^e). (141.5) x=eпервое
уравнение (141.4) дает x*=1, поэтому уравнение (141.5) правильно с x * <^1. График зависимости между tи xв первом сечении представляет собой биссектрису координатного угла от начала до точки/l=x=1(Рис. 218). Затем необходимо построить кривую, используя уравнение■(141.4). При больших значениях x в первом уравнении правая часть может быть проигнорирована: (еx)1—(е+х)1=0. Таким образом, следующее: Икс.. ’- /Т. е———т=х. ■+/! Подставьте найденное значение eдля второго выражения. Получать: .L§ 141J исследование поведения за пределами предела упругости 315 Однако, согласно формуле (139.11),
множитель перед xсправа представляет собой отношение приведенного модуля к касательной., Т=А-х. (141.6) Таким образом, если зависимая кривая между tи Людмила Фирмаль
xизгибает сжатый стержень с нелинейной зависимостью между моментом, заданным графом фигуры, и кривизной 218 изгибает стержень, если прогиб равен v (z), то изгибающий момент в сечении, имеющем координату Z M—P v (z), кривизна оси x (см. 136§ § § -O’(g) кривые это то, что мы пытаемся сделать. х= — р-ЛГ. Перейдем к безразмерным величинам. Получаем:^^m’, 4-x(m*)=0. Критическая сила энгессера-Шериф. н n * EtJ _ l’2et bh’p/ ’3′ Предыдущее уравнение можно записать так: — £ — £yes’ 4_x(yes)= = 0. Найти приближенное решение уравнения (141.7) (141.7). Предположим, что шарнирные
стержни на обоих концах изгибаются в синусоидальную волну, как и в случае упругой потери устойчивости. Потому что изгибающий момент пропорционален отклонению、 Подставляя Tв уравнение (141.6), мы требуем, чтобы это уравнение выполнялось только в одной точке x=1) 2, когда sin^y равно единице. Возьми: — х(М)=0. (141.8)уравнение (141.8) легко решить графически. Для этого нужно оттянуть от начала координат луч с коэффициентом угла, равным P / Ro. Пересечение этого луча с кривой xt-Y1(рис. 218) имеет безразмерный момент и кривизну в средней части стержня-его
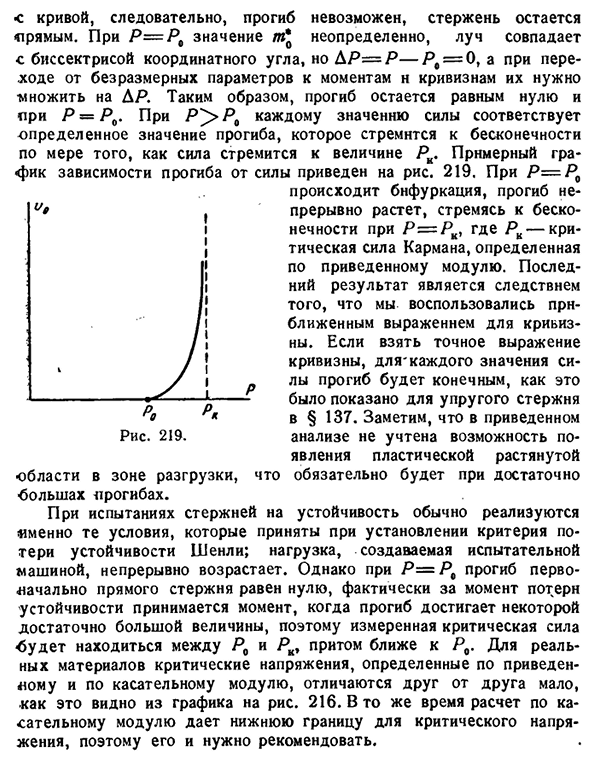
координаты tи x. При PRo, каждому значению силы соответствует определенная величина величины, которая стремится к отклонению, поскольку сила стремится к приближенному графику зависимости отклонения от силы показана на рисунке. Существует ветвь при 219 P=P0, и отклонение имеет тенденцию непрерывно расти и становиться бесконечным при P=P K, где PK является результатом того, что последний результат в критической карманной силе, определяемой приведенным модулем, является использованием формулы приближения к кривизне. Принимая точное уравнение кривизны, для каждого значения силы* отклонение становится конечным, как показано на 137 упругих стержнях. Вышеизложенный анализ учитывает важность пластиковой обвязки, которая,
несомненно, была достаточной для сопротивления, используемого при установлении стандартов для Shanley.- * Зона зоны, большее отклонение для разгрузки. Под испытанием точно те требования, машины устойчивости Teri, непрерывно будут увеличены. Однако если Р=первый прямой стержень равен нулю, то на практике момент потери устойчивости принимается за момент, когда прогиб достигает достаточно большой величины, так что в реально измеряемом материале критические напряжения, определяемые приведенным касательным модулем модуля упругости, мало отличаются друг от друга, как видно из графика. 216. В то же время следует рекомендовать расчет касательного модуля, поскольку он дает нижний предел критического напряжения.
Смотрите также:
