Оглавление:
Кинетическая энергия
Кинетическая энергия материальной точки — это половина произведения ее массы на квадрат скорости 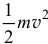 . Кинетическая энергия материальной системы — сумма кинетических энергий всех ее точек
. Кинетическая энергия материальной системы — сумма кинетических энергий всех ее точек
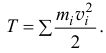
Кинетическая энергия — скалярная и всегда положительная величина, так как 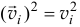 . Для твердого тела формула (15.15) принимает более конкретный вид.
. Для твердого тела формула (15.15) принимает более конкретный вид.
Кинетическая энергия тела при поступательном движении
Так как при поступательном движении все точки тела имеют равные скорости 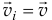 , то его кинетическая энергия
, то его кинетическая энергия
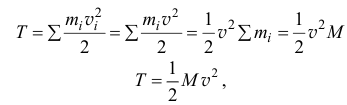
где 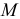 — масса тела,
— масса тела, 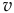 — скорость любой его точки.
— скорость любой его точки.
Кинетическая энергия тела, вращающегося вокруг неподвижной оси
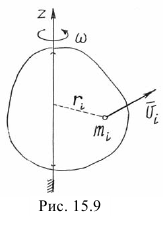
При вращении тела вокруг неподвижной оси скорости его точек 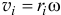 (рис. 15.9). Поэтому кинетическая энергия
(рис. 15.9). Поэтому кинетическая энергия
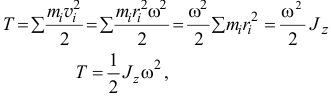
где 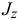 — момент инерции тела относительно оси вращения
— момент инерции тела относительно оси вращения 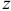 .
.
Кинетическая энергии тела при плоскопараллельном движении
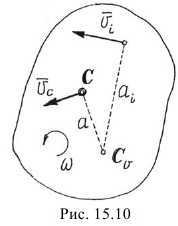
С помощью мгновенного центра скоростей 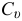 скорость точки тела определяется как произведение расстояния
скорость точки тела определяется как произведение расстояния 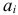 от точки до
от точки до 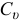 на угловую скорость:
на угловую скорость: 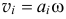 (рис. 15.10).
(рис. 15.10).
Поэтому кинетическая энергия
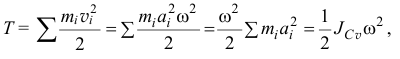
где 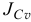 — момент инерции тела относительно оси
— момент инерции тела относительно оси 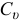 проходящей через мгновенный центр скоростей перпендикулярно плоскости движения. Так как положение
проходящей через мгновенный центр скоростей перпендикулярно плоскости движения. Так как положение 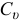 на теле меняется, то полученный результат не очень удобен. С помощью теоремы Гюйгенса-Штейнера (14.4) можно получить более удобное выражение кинетической энергии
на теле меняется, то полученный результат не очень удобен. С помощью теоремы Гюйгенса-Штейнера (14.4) можно получить более удобное выражение кинетической энергии
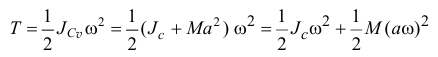
или так как
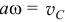
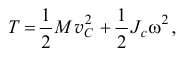
где 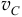 — скорость центра масс тела;
— скорость центра масс тела; 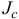 — момент инерции тела относительно центральной оси, оси
— момент инерции тела относительно центральной оси, оси 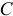 , проходящей через центр масс перпендикулярно плоскости движения.
, проходящей через центр масс перпендикулярно плоскости движения.
Кинетическая энергия тела, вращающегося вокруг неподвижной точки.
При таком движении скорости точек тела определяются как при вращении вокруг мгновенной оси 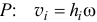 (рис. 15.11).
(рис. 15.11).
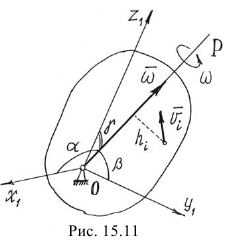
Поэтому кинетическая энергия тела
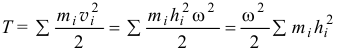
или
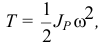
где  — момент инерции тела относительно мгновенной оси вращения
— момент инерции тела относительно мгновенной оси вращения 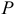 . Конечно, полученный результат не очень удобен, так как ось
. Конечно, полученный результат не очень удобен, так как ось 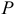 все время меняет свое положение в теле.
все время меняет свое положение в теле.
Если у тела в точке 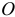 можно отыскать главные оси инерции, то по формуле (14.6) получим
можно отыскать главные оси инерции, то по формуле (14.6) получим
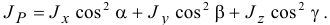
Тогда кинетическая энергия по (15.19) получится такой:
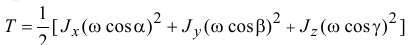
или окончательно,
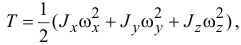
где 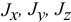 — моменты инерции тела относительно главных осей инерции
— моменты инерции тела относительно главных осей инерции 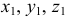 в неподвижной точке
в неподвижной точке 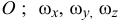 — проекции вектора мгновенной угловой скорости
— проекции вектора мгновенной угловой скорости  на эти оси.
на эти оси.
Для самого общего случая движения материальной системы кинетическую энергию помогает вычислить теорема Кенига.
Рассмотрим движение материальной системы как сумму двух движений (рис. 15.12). Переносного — поступательного движения вместе с центром масс 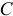 и относительного — движения относительно поступательно движущихся вместе с центром масс осей
и относительного — движения относительно поступательно движущихся вместе с центром масс осей 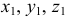 . Тогда скорость точек
. Тогда скорость точек 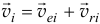 . Но переносное движение — поступательное. Поэтому переносные скорости всех точек одинаковы, равны
. Но переносное движение — поступательное. Поэтому переносные скорости всех точек одинаковы, равны 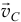 .
.
Значит
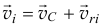
и кинетическая энергия
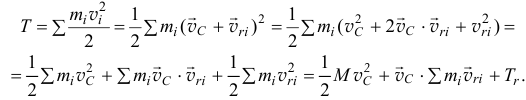
По определению центра масс (14.1) его радиус-вектор в подвижной системе
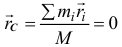
(центр масс находится в начале координат), значит, и
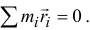
Производная по времени от этой суммы также равна нулю
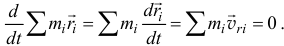
Поэтому окончательно кинетическая энергия системы
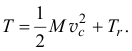
Кинетическая энергия материальной системы равна сумме кинетической энергии при поступательном движении вместе с центром масс и кинетической энергии ее при движении относительно координатных осей, поступательно движущихся вместе с центром масс.
Так, при плоскопараллельном движении по доказанной теореме Кенига формула (15.18) получается сразу, так как относительное движение есть вращение вокруг центральной оси 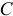 .
.
В общем случае движения тела, которое можно рассматривать как сумму двух движений (переносного — поступательного вместе с центром масс 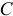 и относительного — вращения вокруг точки
и относительного — вращения вокруг точки 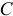 ), по теореме Кенига (15.21) получим
), по теореме Кенига (15.21) получим
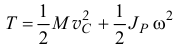
или
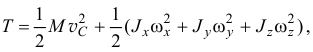
где 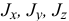 — главные центральные оси инерции тела.
— главные центральные оси инерции тела.
Эта теория взята со страницы помощи с решением заданий по теоретической механики, там найдёте другие лекции и примеры решения задач или сможете заказать онлайн помощь:
Помощь по теоретической механике
Кстати возможно вам будут полезны эти страницы:
| Работа силы в материальной системы |
| Потенциальная энергия |
| Теорема об изменении кинетической энергии материальной системы |
| Закон сохранения энергии |
