Оглавление:





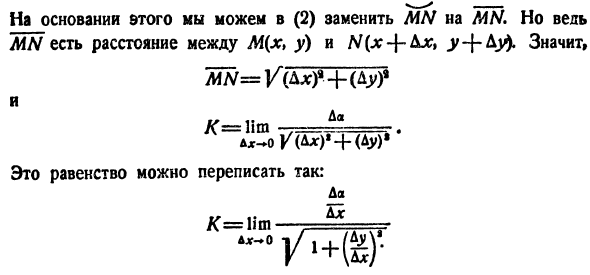



















Кривизна
- Кривизна Н°1.Средняя и истинная кривизна. Здесь вы познакомитесь с кривизной, которая является важной характеристикой кривой. Искривление линии является мерой степени кривизны этой линии. Возьмем линию L (рис. 186).Она сама действует как касательная в каждой точке. Поэтому, когда вы извлекаете любой отрезок AB из L,
касательные L в точках A и B совпадают. Это может быть выражено в том, что направление линии не изменяется при переходе от одной точки линии к другой. another. в точках A и B кривой линии L Я Л Рисунок
In в случае кривых это не так. Если (рис. 187) нарисуйте Людмила Фирмаль
186.187. Если они касательные, то образуют определенный угол 0.Можно сказать, что при переходе от A к B касательная к L (и сама кривая L) стала углом b. величина этого угла поворота Дайте представление о степени кривизны L дуги AB: чем больше угол 0, тем сильнее будет изгибаться L, но само значение угла b еще не работает как мера описанной кривизны above. In дело в том, что если линия
L в сечении длиной 100 см повернута на 50°, или если такой же угол повернут в сечении длиной 200 см, то это уже 1.А 2-й-в половине). Таким образом, значение угла b само по себе не важно, но процент этого угла является средним на единицу длины Дуги Ab. Эти
- соображения приводят к следующим определениям: Средняя кривизна дуги AB линии определения L равна отношению угла 0.Это заставляет касательную L вращаться. При переходе от A к B, вплоть до длины дуги AB Замечание. 1) в Формуле (1) знак угла 0 не учитывается. Угол берется в абсолютном значении. Поэтому средняя кривизна не всегда
отрицательна. 2) единицей измерения угла при расчете КСР всегда является Радиан).Поскольку имя угла опущено в выражении, которое отображает угол в радианах、 Один 188. ** Размер кривизны Длина 1) угол 0, описанный выше, иногда называют углом смежности
(по неизвестным причинам) дуги AJ. Людмила Фирмаль
Нетрудно понять, что одна и та же кривая в разных сечениях может иметь разные средние кривизны(как предполагает сам термин средние кривизны). Таким образом, средняя кривизна дуги АВ рис. 188、 PQ arc. To охарактеризуйте кривизну линии L в заданной точке M, введите: Определение истинная кривизна линии L в нижней точке M является
пределом средней кривизны бесконечно малой дуги, которая сжимается до точки M. Однако обычно прилагательное «истинный» опускается, что просто представляет кривизну линии L в точке M. н°2.Формула расчета кривизны. Спросил. Найти истинную кривизну K кривой y = f(x) в заданной точке M (x, y). Решение. Возьмите другую точку кривой, чем M+>+.Угол, образованный
касательной и осью Ox кривой, зависит от абсциссы точки контакта. Пусть значение этого угла в точках M и N равно a и a соответственно — {- yes. Из рисунка видно, что угол, на который поворачивается касательная при переходе из 189 точки M в точку N, 0,
равен внутреннему углу треугольника ABC C. другой внутренний угол этого треугольника (угол A) СК и-Ж-Д® — внешний угол одного треугольника, не смежных с и С. Таким образом,= 0 +здесь 0 =Да. Таким образом, средняя кривизна дуги у нас равна К-АА Истинная кривизна, K, является пределом этого уравнения. Точка N-это М,
то есть когда Ах да Рисунок 189. Ноль: Нш ™ (2) Ш Чтобы найти это ограничение, рассмотрим следующее:1) BX-Если+ 0, то дробь Да. — R-неопределенность В Да. Нравится 2) при раскрытии такой неопределенности молекула и замещение могут быть заменены эквивалентным значением. 3) крошечная дуга эквивалентна
строке*): Исходя из этого, вы можете заменить WE на MN в (2).Но понятие MN-это расстояние между M(x, y) и N (x-f-Ajc, y-f-Ay).Значение Ж = +(ДУ) 1 К = \ им K (4ds) » +(Au) ’это равенство может быть переписано как: Да. К = Лим— = м = (Ничто не мешает вам
рассматривать Ajc> 0, но это вовсе не проблема, потому что в выражении K она касается только абсолютного значения этого выражения.) К АС.#. АА ээ£ = г * > БВ и = * Х- Значение (3) помните, что это tga = y’X. дайте 0, поэтому перед радикалом нужно выбрать символ -} -.Таким образом, y = YR -««• — Jq не. Следовательно, Vx = — rr = t. вторая производная дает V ^ x. знак минуспоследнего выражения
отбрасывается, так как y’X должно быть получено только в абсолютных значениях. Тогда из простого преобразованного выражения(4) (6) К-5-、 То есть кривизна окружности во всех ее точках одинакова и равна единице, объединенной радиусом
окружности*). П°3.Для параметрических заданий. Кривая задается параметрическим уравнением (7 )) йк = СР(0, мл = Т <0. предполагая, что уравнение (5) определяет зависимость y от x, как видно из N°5§ 3、 Э-э-Т7 ″ э-э-ГТЦ Подставляя эти величины в уравнение(4), получим кривизну K、 Икс? к = ’ M1G После некоторого упрощения、
(Я) к = М \ Х \ -У \ Х] Это формула для кривизны параметрической curve. As как уже говорилось выше, правильнее писать ( | ) в числителе дроби. г Форекс!- y \ xf|, чтобы быть всегда/ C ^ 0.Точка выпрямления кривой(7) по-прежнему характеризуется уравнением K = 0.Образцы. Найти кривизну эллипса х = подкараулил, у = bsint В этот
произвольный момент. Решение. Из (9) х \ =- грех ты Г \ = пожелать/, х \ Т = — соз/, г ’=-£грех Подставляя (8)、 к = ab (а * грех не-}-б * cos8 т)*, н — В частности, для точек, соответствующих значению/ = 0(a, 0)、 К = = = Т *- Н * 4.Для полярных координат. Дайте кривую по уравнению r = /(0) (10)) В полярных координатах. Возьмите любую точку на этой
кривой. если X и y-декартовы координаты、 l = R cos0, y = R sin b. (11) Но ведь согласно (10) задача y d 0 также определяет значение r. таким образом, область b полностью определяет координаты x и y. So, уравнение (11) (где r означает функцию (10)) является
параметрическим уравнением кривой. Но его кривизна определяется формулой (8).Вычисляет количество, содержащееся в этой формуле. так как r-функция от 6、 x ’% = rj so 0-поводья 0, Jfj «RJ $ M + ЛГ | = Р / соевые 0-2г£грех 0 — * р, потому что б, Ил-Р | грех 0 + 0-р sin0.Здесь мы находим значки опущенных r {и rj 0 для краткости. ХХ ’— y \ x \ =
R9 + 2m » — RT. (12) Быть Наконец. г «4-2г»-гг ’>(Ф + ryi» Образцы. Найти кривизну кривой r = * A, где r ’= r «=I. n°b. окружности, центры и радиусы кривизны. Малую дугу кривой линии L можно почти заменить отрезком линии, касательной к L в определенной точке рассматриваемой дуги. Если есть интерес к длине дуги или
ее направлению, такая замена допускается. Однако кривизна прямой линии равна нулю, поэтому она явно неприемлема при исследовании кривизны дуги. Если вы хотите грубо заменить дугу кривой L дугой более простой линии, проблема, связанная с кривизной линии L, требует, чтобы вы взяли что-то вместо линии замены. 191 и более. Очень естественный Нарисуйте круг для этой цели. Когда эти
соображения развиваются, мы приходим к следующему определению: определение. Окружность кривизны кривой L в данной точке M является окружностью(рис. 191) 1) пройти через точку M\ 2) M имеет общую связь с C 3) кривая в точке M с той же кривизной K, что и L. 4) Центр C на стороне кривой L. кривая L вращается своей вогнутой
поверхностью (точка M).Давайте рассмотрим это поближе definition. As для кривизны кривой L мы упомянули, что мы говорим о кривизне точки Af, потому что в любой кривой кривизна отличается от точки к точке. Поскольку кривизна окружности во всех точках одинакова, мы не говорили, что она означает кривизну в точке M, как для
окружности кривизны. Кроме того, поскольку окружность касается кривой L в точке M, ее центр C является нормалью кривой L в точке M. радиус кривизны окружности R можно легко вычислить, каким он должен быть. То есть, с одной стороны, кривизна этой окружности должна быть равна кривизне K линии L в точке
M. Кривизна является i. So f(= 4-и (13 )) Это значение называется радиусом кривизны кривой L в точке M(так как в разных точках радиус кривизны кривой L разный, нужна ссылка на точку! это не. Кроме того, центр C окружности кривизны называется центром кривизны кривой L в точке Af. Конечно, все вышесказанное применимо, когда точка M не является прямой точкой кривой
L. In в этом последнем случае K = 0, и нет круга с такой кривизной. Условно, в точке линеаризации кривой L окружность кривизны вырождается в прямую линию (то есть становится касательной L в рассматриваемой точке).Поэтому говорят, что в точке коррекции,
радиус кривизны равен бесконечности, а центр кривизны удаляется до бесконечности. Образцы. Построить центр кривизны параболы Один Его вершины(0, 0). Из уравнения линии высвобождения материала, yx = x, yx = 1• Итак, K = — tm. И если x = 0, то можно видеть, что K = 1.И так оно и есть.、 (+икс’ )* » (13) к R = 1.In кроме того, поскольку парабола вершины является касательной к оси Ox, центр кривизны C находится на оси Oy и выше Ox axis. So, центр окружности
кривизны равен C (0, 1), а радиус равен R = 1. 192 вы можете видеть, насколько близки парабола и ее окружность кривизны друг к другу. Учитывая малую дугу кривой U, содержащей точку Af, можно приблизительно считать, что эта дуга является дугой окружности кривизны(линия L точки Af).Поэтому мы снимаем вышеупомянутую
дугу в другой точке N, которая отличается от Af, но потому, что она очень близка к Af (потому что дуга должна быть маленькой!).), Af и N можно считать находящимися на одной окружности в контакте с кривыми L и Af (точно) и N (приблизительно).Однако центр C этой окружности должен находиться непосредственно на 2 нормалях I, нарисованных через Af и M, то есть точках пересечения этих
нормалей. Это соображение не только обеспечивает относительно простой способ нахождения центра с чертежа приблизительно, но и приводит к возможности другого определения центра кривизны. То есть ошибка, возникающая в результате замены дуги кривой на дугу этого круга кривизны, меньше, чем дуга shorter. In другими
словами, если взять точку M на кривой L и точку N рядом с ней и найти точку пересечения нормали, проведенной от Af и M до L, то получится более точный центр кривизны C (точка Af), где N ближе к Af. Поэтому вы можете дать определение. Центром кривизны кривой L в заданной точке Af, C, является предельное положение
пересечения нормали через Af и нормали через бесконечно близкую точку N. Это определение позволяет по-новому продемонстрировать всю теорию кривизны. То есть, поскольку мы знаем, каков центр кривизны кривой L в точке M, мы можем использовать формулу M R = СМ И тогда мы вводим понятие кривизны/ C К = = 7т ’ n°b. концепция
эволюции и involute. In выше мы обратили внимание читателя на то, что говоря о центре кривизны с любой кривой, нам нужно указать, для какой точки м кривой точка С является центром кривизны. Это приводит к следующему определению: Геометрическое положение центра кривизны линии определения L называется вырождением
этой линии. Сама линия L называется эвольвентой ее Эволюта*). Ясно, что прямая линия не имеет Эволюта, а точка является осевой линией circle. In в других случаях некоторые линии служат эволюциями. Образцы. n * 4§ 3 определил понятие эвольвенты в a circle. It показано, что эта линия на самом деле действует как
Эвольвента в введенном смысле, то есть круг действует как ее эволюция. Для этого используйте точку M (t) эвольвенты окружности, чтобы найти нормали, которые проходят через M и достигают involute. As мы видели, что параметрические уравнения эвольвенты являются: х = р (потому что т-ф-1 грех Т), Г = Р(греха Т — * потому t). Отсюда х ’Т = РТ потому t, г’ Ф = #ц \ НТ. (14) Так… учитывая, что t-угол наклона луча OB к оси Ox (рис. 185), становится ясно, что
касательная к эвольвенте в точке M параллельна радиусу OB, а Нормаль перпендикулярна OB. Но из M можно опустить только 1 перпендикулярно OB, и это поток MB. Таким образом, MB становится искомой нормалью центра кривизны эвольвенты в точке M. Теперь
найдем радиус кривизны эвольвенты. Согласно (8), кривизна эвольвенты равна _ yjx ’ т-г’txi Но из(14) ДГ; = /?(соб * — t sin 0,#=#(sin t + tcost). Если вы назначите это (15)、 — з И. Поэтому радиус кривизны эвольвенты в точке M равен Rtt, то есть длине участка резьбы Mb. It сразу видно из рисунка, что точка B нити накала из окружности
находится на стороне эвольвенты, которая вращается вогнутой, поэтому ясно, что B будет центром эвольвентной кривизны в точке M. поскольку различные положения точки B заполняют окружность, она служит в качестве эвольвенты круга и эвольвенты. Попутно
мы установили, что нормальный MB для эвольвенты связан с эволюцией соответствующего центра кривизны. Ниже показано, что это всегда так. н-7.Координаты центра города curvature. It возникает задача нахождения центра кривизны c координатой (x0 yy) кривой y = f (x) в точке M (x: 0, y0) этой кривой. Решение этой задачи основано
на следующих 2 соображениях: 1) точка C находится на нормали кривой y = f ( * ) через точку M, 2) расстояние от M равно радиусу кривизны/так как точка C находится на нормали кривой y = f ( * ). Нормальные уравнения г-СС^ -<* — * * >• Тогда первое соображение дадим xc — = — Yo (Us —Yo) ’ 2-е рассмотрение、 Где находится радиус
кривизны?(13) и (4). Примите форму (17) (ДГС-ДГ.) ’+(yy-y.) ’=(1 ″ U. здесь подставляется xc-dg, а из (16), pay (Us-A) W +(Us-Y’) ’= (yce + yif, уменьшаясь с ’ Y * 1 Кишащий с-Л -±!±* 5(.Восемь) Вау. Осталось выяснить, какой из 2-х персонажей выбрать. Различают 2 случая.1) кривая y = f(x) в точке M изгибается вверх вогнутой поверхностью, а 2) вогнутой поверхностью изгибается вниз к M. In случай I) V! Понятно,
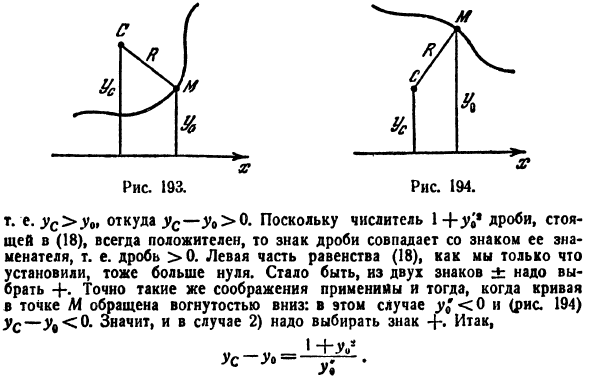
что там > 0, и далее на рисунке 193 точка С находится выше точки АФ. Рисунок 193.Рисунок 194. То есть yn> y0, а ync-y0> 0. (18) числитель дроби 1 + ^ *всегда положителен, поэтому знак дроби совпадает со знаком знаменателя, то есть дробью> 0.Левая часть уравнения (18), как мы установили ранее, больше нуля. Поэтому вам нужно выбрать
2 символа±.Точно такие же соображения применяются, когда кривая в точке M направлена вогнутой вниз surface. In это дело, y! <.0 и<рисом * 194) таким образом, в случае 2) следует выбрать знак»+».Так… В-В-1 Нам Г°• Назначьте эти значения в (19) и опустите индексы для x9,y0 и y’Y для краткости. 。 , х \ * + г? 。 Используя
формулу (19)、 Теорема * Нормаль эвольвенты связана с эволюцией соответствующего центра кривизны. В самом деле, если координаты точки M просто обозначаются x и y, а точки C обозначаются 6 и tj, то уравнение (19) принимает следующий вид: т = х-г ’ щ, ч = г +в.(20 )) Куда? М = я±У1 Звезда.、 Отсюда (16) до конца Если начальная кривая
задана параметрически、 Год. * .. Г \ х \ — у \ Х1 Вау. икс’ ; Уравнение (20) является параметрическим уравнением Эволюта(ведь|и ij-координаты любой точки Эволюта).В дальнейшем、 Счетчик х. Угловой коэффициент касательной к Эволюте равен i (указывая производную по параметру G) Г ’+ О’ Х Т-4- ? 1/’<?-/ <? »
Но непосредственно из (21) y’<?= 1 + г’*.И так оно и есть.、 t_ в / + <? ’__1 В Это означает, что касательная эвольвенты в центре кривизны C параллельна нормалям эвольвенты в соответствующей точке M. Однако обе эти линии (рис.195) проходят через C, поэтому они совпадают по мере необходимости. И * 8.Железнодорожное
округление. 1. объясните применение понятия кривизны в одном техническом вопросе. Из механизма, известно следующее. 1) точка L4, которая равномерно движется со скоростью v вдоль плоской линии L, имеет ускорение t » = do1 в каждой точке. Где K-кривизна линии L в точке, где точка M находится в этой точке. (Называемые нормалями)
ориентированы перпендикулярно A от точки M до соответствующего центра кривизны. Если линия L является прямой линией, то/ C = 0 и нормального ускорения нет. 2)Если в точке движения M имеется масса t, а в определенный момент времени имеется ускорение w,
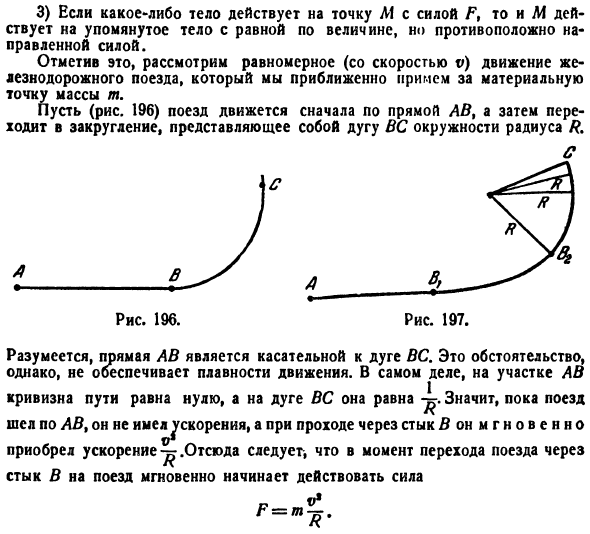
то в этот момент сила F = mwt действует на M в том же направлении, что и ускорение W. Слиента Рисунок 195. 3) Если какой-либо объект действует на точку M с силой M, то M действует на вышеупомянутый объект с равными, но противоположными по величине силами. Обратите на это внимание и рассмотрите равномерное (при скорости v) движение железной дороги trains. It принимает почти как материальную точку масс М. (Инжир. 196) предположим, что поезд
сначала движется по прямой АВ, а затем движется по окружности, которая является дугой радиуса R. И Конечно, прямая Ab является касательной к дуге самолета. Однако плавное движение в этом случае не гарантируется situation. In факт, раздел AB Кривизна пути равна нулю, а на дуге солнца она равна Я шел по АВ, но скорости не было. Пройдите через переход B и немедленно По этому, в момент
прохождения поезда Узел B поезда скоро начнет излучать силуВозникновение такой мгновенной силы называется ударным явлением. Поэтому в тот момент, когда поезд проходит через узел B, поезд получает удар Ft со стороны рельса. Это означает, что поезд сам даст такой же удар по рельсам. Масса поезда и его скорость v обычно очень велики, поэтому вышеупомянутые явления могут испортить полотно и даже вызвать крушение поезда. Чтобы избежать
вышеуказанных проблем, вставьте»кривую перехода» между ними, как показано на рисунке, без непосредственного соединения прямой и круговой частей пути. 197 линий£i#s Эта линия выбрана так, что кривизна K непрерывна. = = — Увеличение точки B из точки Bt/ C =0 Это обеспечит плавную поездку на поезде. Поскольку точка Bt должна быть линейной точкой линии BtBv, нет линии, которая может быть
выбрана в качестве переходной кривой, но существует только 1 Линейная точка. Например, нормальная парабола y = ax *не подходит для этой цели. Здесь нет линеаризации » — 2af0n point. In напротив, кубическая парабола y = ax9 имеет точку выпрямления * = 0, и поэтому фактически используется в качестве переходной
кривой. Интересно, что такое, казалось бы, абстрактное понятие, как точка прямолинейности, имеет важное практическое применение.
Смотрите также:
| Направление вогнутости кривой | Общие приемы интегрирования |
| Параметрическое задание кривой | Интегрирование рациональных функций |
