Оглавление:

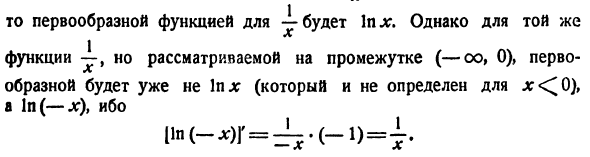







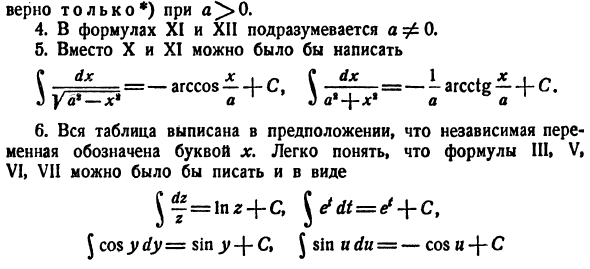











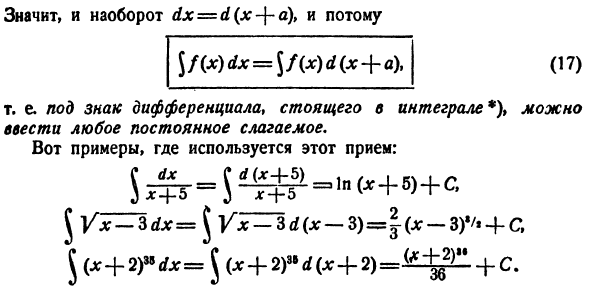





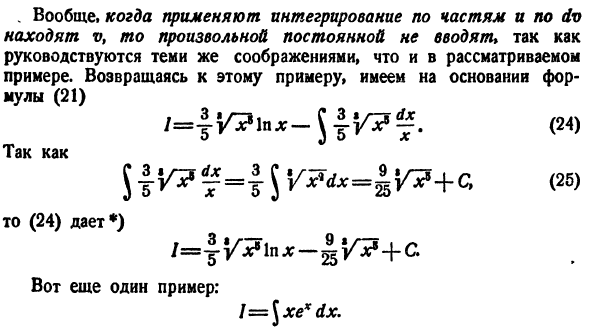



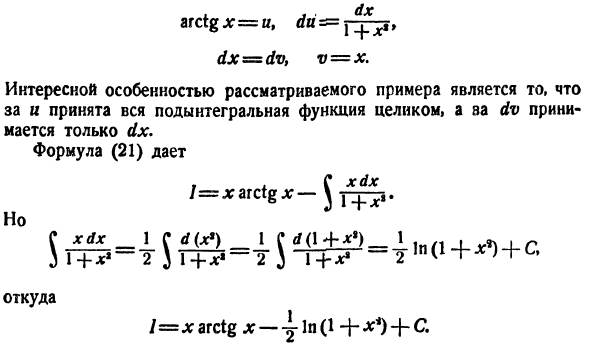



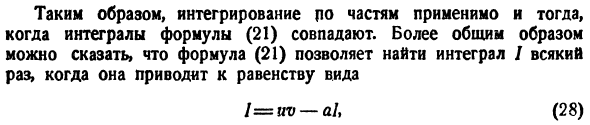

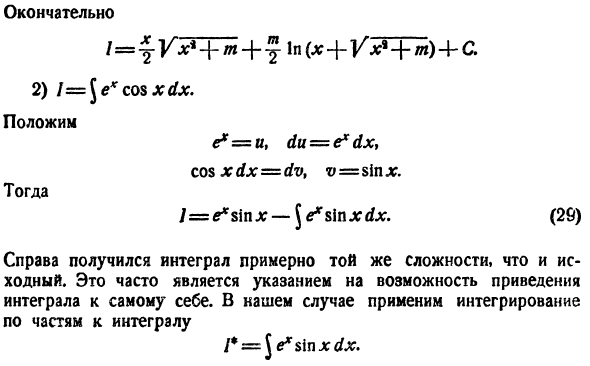



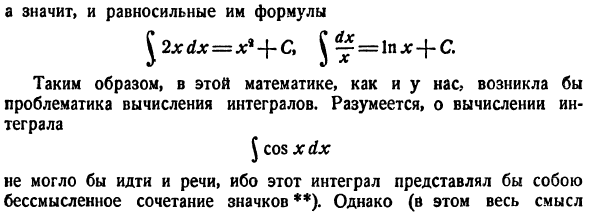
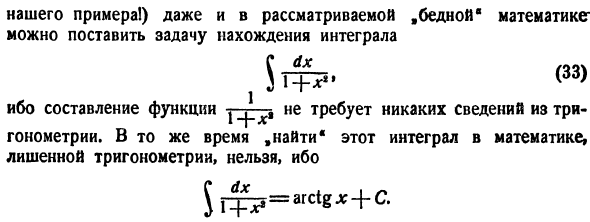

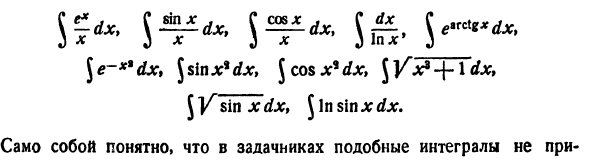


Общие приемы интегрирования
- Общие методы интеграции Н°1.Анти-производные. Основной задачей дифференциального исчисления является нахождение задачи дифференцирования, то есть скорости изменения function. In практика, часто важно решить противоположную проблему. Знайте скорость изменения (относительно аргумента) функции
и найдите это function. In другими словами, здесь нужно знать производную и найти функцию. Эта операция называется интеграцией. Мы определяем этот термин более подробно. Функция определения F (jc) называется обратной производной функции/ (), если последняя функция является
производной функции F (x F(х)= F(х). Людмила Фирмаль
Например, x9 является обратной производной от 3x, для(jc® / = точно Кроме того, в ГД находится обратная производная от -. икс Действие нахождения обратной производной функции f (x) называется Интегралом от этого function. So вверх Интеграция 3xi、
dt Замечание. Вы, возможно, потребуется конкретно указать интервалы, которые определяют функции, которые должны быть интегрированы. Например Если мы будем думать о функции-интервале (0,+ oo), то обратная производная функция-будет в.Впрочем, то же самое — Примитивная функция будет находиться
- в.Впрочем, то же самое Функция, но сначала учитывается в интервале (- oo, 0) Форма больше не находится в jc (она не определена для 1n (- x). Напротив, функция x3 действует как обратная производная от b на всей вещественной оси (- oo, — f -°°) (и на любом из ее сечений). Естественно возникает вопрос: имеет ли каждая
функция f(x) антипроизводную функцию? То есть все функции f(x) являются производными от других функций. Ответ Теорема если функции непрерывны на определенном интервале, то функция имеет примитивы. Не доказывает эту теорему. н°2.Любая константа. Неопределенный интеграл. Я уже упоминал ранее, что функция
3jc4. Если Y = ZdA, то z = + 5 также примитивно, так как m. Людмила Фирмаль
является обратной производной от = 3x \в общем случае все функции имеют Вода Zx , следовательно, является примитивом Zx9.In в общем случае, в дополнение к F (x% является обратной производной от/ (), любая функция F(x) -\ — C также имеет обратную производную от f(x \ for
[Ф(Х)+ СГ = F ’(Х) = ф {х). Задача возникает естественным образом: является ли множество всех контрпроизводных некоторой функции f (x), ограниченной формулой вида Ф (Х)+ с, (1) Где F (x) — 1 из них, или y /(x) имеет примитив, который не может быть получен из(1)для постоянного значения C. ответ таков: Нет никакого f (x) в любых
примитивах, кроме теоремы (1). Действительно, пусть F (x)-некоторая непроизводная от f (x)= f (X), но f ((1) также является обратной производной от x (x), следовательно, F (x)= f (x).Введем разность F (x) ・F (x) и обозначим ее через β ( —). К(Х)= Ф [(Х) — Ф(Х)= Ф(Х)-Ф (Х) — ф (х)= 0. Исходя из известного знака постоянства функции,
из соотношения R (x)= 0, можно видеть, что R (x) является постоянной величиной. Обозначим эту константу через A: R(x)= A. тогда F (x) — F (x)= A и Фи(Х)= ф()+ А Другими словами, для доказательства значения C = A функция F ((x) является производной от (1). Таким образом, (1)является общим представлением или, как
иногда говорят, полным антипроизводным семейством f (x). Если определение F (x) является обратной производной от f(x), то выражение /•(*) +С. Где C может принимать любое постоянное значение и называется неопределенным интегралом функции f (x)、 \ Ф (Х) DX. (2) Следовательно, равенство \ F (х) dх = F (х)+ с(3)
Существует только другая нотация для отношения F (x)= f (x), или отношения dF (x)= f (x) dx, что одно и то же. Причина, по которой фактор dx вводится в символ (2), объясняется ниже. Кроме того, член C, содержащийся в правой части(3), называется любой
константой, а функция f(x) называется подынтегральным выражением. Читателю легко проверить правильность этих отношений ^ exdx = Е *- \ — С,^ в COS xdx = Sin х + С, й xdx =—\ — с、 Каждый из них является описанием определения, которое мы только что показали. Равенство. Яш-Би * + с Он также показывает
определение, но только для x> 0.Если это так Определение неопределенного интеграла подразумевает следующую теорему: производная неопределенного интеграла равна подынтегральной функции, то есть, (4 )) Фактически уравнение y = J f (x) dx, y = F (x) — \ — C、 где 1 из примитивов f (x), где C = const, но Y = F(jc)= f(.* ) При
необходимости*).Правила основаны на одном и том же определении. Как проверить равенство или нет (5) $ /(.х) dх = Ф(Х)+ с、 Если I (x) — это некоторая функция, вам нужно различать правую сторону. Если вы получите подынтегральное выражение слева, то (5) будет истинным. В противном случае(5) является ложным. Образцы.
Пожалуйста, подтвердите (6) _ Э * + т + х Ух * + МДж х + ый?+ М#ЧХ * + м Один Один / = Vx * + m и (6) будут доказаны. П°3.Таблица майора integrals. To для разработки интегрированной функции необходимо знать следующие 13 формул: г = \ п(х-\ — ЧХ%+ м) — \ — с、 Предположим, мы нашли/ =отсюда Один х + т ’+ т И. \ ДХ = х-\ — С.
VII Устава. \ грех xdx = — COS в йк + с фунт JX используется-Л2 — + с восьмого. = + $ Ф = м * + с. іх. Дж-г — ^ — cigx + С. $ е » РЧ * = * * + г ХL = + III. IV. В. ВИ. Jcos * <Ф * = ХН * + с ХІІ. ХІІІ. = + Проверка каждого выражения может быть выполнена в соответствии с правилом n°2.It необходимо выделить правую часть выражения и убедиться, что подынтегральная функция слева взята. Эта проверка
предоставляется читателю. Замечание. 1.Формула II применяется к af-I. In дело в том, что если a = −1, то правая часть выражения теряет свой смысл. если a = — I, то место уравнения II занимает уравнение III. 2.In уравнение III, это означает x ^> 0.* Если <0,
то вместо III、 $£= 1n (-*)+C. оба этих выражения можно заменить на 1. Аналогичным образом, выражения XII и XIII могут быть записаны в более общем виде. Jdx по-1, х-я Я Я 3.Выражение X означает a]> 0.In факт, для Φ0 Но трансформация * ) Применяется только к a> 0. 4.In выражения XI и XII, это означает af 0. 5. Вместо X и XI、 С*£ =-«» *» ^ + C — ^ _ = — Iarccttg ^ + C Дж г А9-х * Е А *- \ — х *
а а 6.Вся таблица описана в предположении, что независимая переменная обозначается буквой x. It легко понять, что выражения III, V, VI, VII могут быть записаны в следующем виде $ Г = ЛНЗ + С,^ Е? ДТ = е? + С、 Джей, потому что ыды-грех г — \ — с, jsintt (/«=- COS и-Ф-С Точно так же выражение Я может быть записано в любой форме. \ ДЗ = з + ст \ ДТ = т + с,\ ды = г — -с> \ дю = ю + с Вышеизложенное позволяет
понять, почему неопределенный интеграл от/(x) описывается в виде (2). $ /(). (7 )) На самом деле, если вы возьмете обозначение (7), вы понятия не имеете, чему оно равно J 1.%Z, равный x%для t, зависит от того, какой из них Символ обозначает независимую переменную. Назначение коэффициента dx в Формуле (2)заключается в точном
представлении независимых переменных. N°4 полная интеграция и устранение постоянных факторов. Если вы интегрируете почти постоянно, вам нужно использовать 2 теоремы, которые доказываются в этом разделе. Интеграл алгебраической суммы некоторых функций равен алгебраической сумме интегралов этих
функций, то есть,、 Доказательство. (8)чтобы отличить правую часть этого уравнения, чтобы проверить правильность. Однако показанная правая сторона является алгебраической суммой нескольких членов. Следовательно, в результате дифференциации、 ($/() ДХ) ’ + {\г (х) DX)’ — {\х (х) DX). (9 )) По теореме n°2、 {\ F (х) ДХ)= ф(х
[\ г (х) DX) ’ = г(х), (\ч (х) DX)’ = ч(х г Итак, поскольку (9) есть не что иное, как f(x) — \ — g(x) — h (x), производная справа от(8) становится неоткрытой функцией слева от того же уравнения, если это необходимо. Доказать это. Теорема 2.Постоянные факторы могут быть извлечены из интеграла symbol. In другие слова、 (10 ))
Доказательство очень похоже на предыдущее. Точно, ставлю Г = А \ Ф (Х) DX、 Продолжать. Г = {А \ Ф (Х) DX) ’= а(\ Ф (Х) DX]’=: ФП {х)、 (10) докажите. Образцы. 1)/ = $(2х»+ 9л:-5)ДХ = 2] х * ДХ- \ −9 \ xdx-б \ ДХ. Все 3 интеграла справа являются табличными. Значение Или Где c = 2Ci-}-9Ci-5C8 предполагается. Обратите внимание, что обычно
требуется вычислить отдельные интегралы, которые появляются в правой части отношения \ [ФП (х)- \ — БГ (х) — ч (х)] dх = А \ Ф (Х) DX + Б \ г (х) DX-с \ З (х) DX、 Любая константа не вводится, но 1 константа назначается в конце всего вычисления. = 2JC9 + 12jc-4-91njc + C 3 > Hsfe- Позже вы узнаете очень простой способ вычисления этого интеграла. Вам придется прибегнуть к искусственному приему, используя
ненавязчивую информацию из технологии интеграции, которой вы в настоящее время владеете. Именно так. Я-ЦДХ −1 и 1 исправление-1Cdn’х + atfx Дж 4 sin8 * потому что * Х 4 Дж sin1 * потому что* а4 Джей грех «л: потому что’л: Еще проще: П°5.Метод замещения. Вот как заменить, что является очень важным способом интеграции (это также способ замены переменных). чтобы понять этот момент, сначала рассмотрим несколько примеров.
Предположим, вам нужно вычислить Интеграл / = J и Е * * топор потому что Х DX. (11) cos xdx = d (s \ n x), поэтому/можно переписать в следующем формате: грех х). введите новую переменную r, установив sin x = z. а затем… Справа находится табличный Интеграл (формула V). Итак… + С Осталось вернуться к старой переменной x、 Достоверность полученного результата легко проверяется
дифференцированием. Рассмотрим другой пример. Позвольте мне. I-J — (12)) И затем… / =(* „<“ <Ф (arctgjc)、Или Где: 2 = arctgx. Я найду его здесь. / = = » ? ’+С == ?[З + J на клавиатуре, потому что 2zdz \ ^ потому что 2zdz = Дж ^ cos2zd(2z паза)= ^—\ — С. Остается вернуться к старой переменной x. по этой причине z = arcsin^, sin 2z = 2(?Грех з) (), потому что по Z)= 2х ВР *- Подобный этому / =
Г арксинуса / ДПГ ^ + с В заключение мы покажем, как табличное выражение XX получается методом подстановки. Позвольте мне. Впустить меня. Откуда Я = [ДХ Х% — \ — м = з xdx xdx ДЗ = м dz_dx х ~~ Z и Е Чтобы получить, перейдите к производному проценту с dx _dx с + dz_d(х + з) г ХL-г * Так… н°б. Линейная замена. Обратите внимание на 2 особых случая подстановки переменных. I.
добавьте константу под производной. Для любой константы a Д(х — \ — а) * = ДХ. Вот почему dx = d(x-f-a) и поэтому (17 )) То есть под знаком производного состояния Интеграла*) можно ввести любой постоянный член. Вот пример того, где эта техника используется: Дж ЧХ ключа-IDx = Дж ух-1д (х-3)= |(ЛГ-3) ’/ » 4-с、 (Л + 2) » ^(x + 2) Mcfx = ^(x + 2) 3,)、 С ^ -IJ и ^ — ИЖ ^ — ^ + Д +
С (18) в N°7.Интеграция компонентов. Существует еще один широко используемый метод, называемый консолидацией. Первый пример можно решить следующим образом: С дх ДХ ЛФ _ если»( + ’/、)_ 1/7 \ J4 не ^ + 7-4 б + з+’/, 4 ^ 4 Дж ’ На первый взгляд, ответ другой. Однако, 4l:+ 7 = ^ +4.И так оно и есть.、
устаканится(4х + 7)= Иос(х+|) + / ln4.Дело в разнице между константами C и C’.С’ = 1Н + 4 с пусть u и v-2 функции аргументов x с производными u ’и xL. (uv) ’ = u’v-f-them/. Это уравнение есть не что иное, как тот факт, что произведение uv является примитивной функцией суммы u’V—uv.И так оно и есть.、 ^(u’V — {- ui/) dx = uv — \ — Ct Откуда ttvdx — \ — \ mfdx = УФ + С(19) Но urdx =
du, 1 / dx = dv и поэтому(19) можно переписать в следующем формате: J v du-f-J и dv = uv-j-C переместите первый Интеграл вправо. Дай \ ВДС = УФ-Джей-Orft + с (20) Поскольку Интеграл J vdus уже содержит какие-либо константы, можно также включить в (20) член C. в результате для каждой части получается интегральная формула Это выражение является
допустимым идентификатором для любой пары функций a и V. иногда (конечно, не всегда) правый Интеграл (21) проще, чем левый Интеграл. Тогда имеет смысл применить формулу. Рассмотрим подробнее структуру формулы (21).При переходе к правому интегралу коэффициент a левого интеграла
заменяется на du. То есть она дифференцирована. Другой фактор dv из левого интеграла заменяется на vt. То есть он является интегральным).Если мы обсудим это абстрактно, мы можем ожидать, что упрощение интеграла происходит от одной из этих 2 операций. Однако в большинстве случаев, встречающихся на практике, упрощение обусловлено
дифференциацией factors. So, если подынтегральная функция имеет фактор, упрощающий дифференцирование, примените формулу (21) и замените ранее упомянутый фактор на И, и все остальное(dx! Вы должны использовать это как dv. Например、 1 = VU1?\ ПХ <1х. Подынтегральная функция содержит фактор,
производная которого намного проще, чем она сама. Поэтому мы предполагаем, что 1plg = Н Т * ДХ = ДВ. Отсюда сначала получаем = J и в MFJ? ДХ * = ^ вю? + С. (23) Но ведь(внимание! Я хочу использовать свою идентичность (21). для этого не обязательно включать весь набор функций (23), но достаточно использовать один из них-1.Конечно, самое простое-это взять
функции, соответствующее значение c — О. другими словами、 3 ″ / — т 。В общем случае никакие константы не вводятся, так как применяется интегрирование по частям, и если v находится по dv, то он руководствуется теми же соображениями, что и примеры, принятые во внимание. Возвращаясь к этому примеру, он основан на Формуле (21). / = фи /(24) С тех пор (24) дают*) Другим
примером является следующее: л = \ Хе * ДХ. Здесь единственным элементом, упрощающим дифференциал, является x. возьмите и составьте таблицу х = у, ду-ДХ、 е * ДХ = ДВ в = е*. Используйте (21), чтобы получить L = xex-\ e * dx = xe *-+Интеграл вычисляется аналогичным образом л = \ х * cosxdx. Здесь. x * =и du = 2xdx, cos xdx = dv, v = = ■ sin x И LХ = х * Sin х-2 \ хз \ nxdx. (26)
Неотъемлемый. / , = ^ Х Sin xdx Проще оригинала (тот факт, что cos x был заменен на sin x, не играет роли»и вместо коэффициента X% есть простой коэффициент x \ K Y]. х = у, ду = ДХ、 грех xdx = ДВ в = — а . Дай / я = — Х, потому что Х — \ — J не потому, что xdx = — х,
потому что Х — | — sinx-\ — с Если вы замените (26), Вы в конечном итоге найдете () / = Jitr ^ Sin х — \ — 2х, потому что Х-2sinjp-й-с Полезно вспомнить следующие 6 типов интегралов. Это полезно для расчета по компонентам интеграции. И. \ х * е * ДХ, ИЖ. [х° \ nxdxt Ил Дж Xya грех х DX, В. Дж Xya arctg х DX、 III. JJ ^ cos xdx, VI. JC » arcsin xdx. Для интегралов I, II, III коэффициент Xя следует интерпретировать следующим образом: это приводит
к аналогичному типу интегрирования, но уменьшает показатель X на 1.После применения этой техники я раз、 Получите 1 из таблицы интегралов ^ е * ДХ, Jsinjcrf*, \ в COS xdx. В интегралы в IV, V и VI дифференциации, трансцендентные факторы представлены в упрощенном виде(т. е.\ ПХ, arctg *или arcsinjt).Оно должно быть принято. Вот несколько примеров
из вышеперечисленного. 1) / = j в jcarctgxdx. Здесь. arctg л; = у, ду = Дж-qrjs、 икс * xdx = ДВ в = — 7Т、 Откуда 。 икс.» случай x * dx I =-2 * rciZx — » T J TTTI * \ + Х1 Последний Интеграл вычисляется следующим образом: J Т = $ szg1 *-$(•■ Значение / = г равенства arctg х-ж + ^ АР ct6 * + с 2)/ = J из равенства arctg xrfjc. Здесь. DGX по АГ = ут ДХ = ДВ, в = Х. Интересной особенностью данного примера
является то, что целая подынтегральная функция считается k, а советник dv считается только dx. Формула(21) Но… Си ^ — МФД ^ — ИЖ’ — ц ^ — к + МК Откуда / = xarctgx—ЛН(л+) +£ Вот еще 2 примера с той же функциональностью. 3) I = \ nxdx. Я тебе верю. , Нум ДХ = и, Дю = — Т ДХ = ДВ, в = Х. Отсюда Я = Кин ЙК — ^ х <£= х \ ПХ-х + с 4) / =
J arcsinjtrrfx. Я тебе верю. арксинуса * = ч, ду-7 = = 、 В1 — * Е ДХ = ДВ, в = Х. Отсюда / = * арксинуса * — $ г = г- Отель П лгг / л:1 г =(—р = J 2 J 2 J 2 3 / GG = T » 1 Значение Я = xarcsin + \ —х V * + сЭто равенство верно, но оно бесполезно, потому что правый Интеграл более сложен, чем левый. n°8.It приносит интеграл к itself. In выше, рекомендуется
применить интегральную формулу к детали ^И ДВ = УФ — ^ ВДУ(21) Если правый Интеграл проще левого. Однако вы можете обнаружить, что правый интегратор является именно левым интегратором. Например、 я = Дж ^ ХХ. Пожалуйста, положите его сюда) 1х х = у, ду = Д — ±т — = ДВ, где V = \ ПХ. Тогда уравнение (21) имеет вид С правой стороны вы получаете оригинальный Интеграл/. So … / = 1n9lg-а(27)
Здесь♦) 2 / = ln4jc + с И Следовательно, интеграл по частям также может быть применен, если Интеграл в уравнении (21) matches. In в более общем виде выражение (21)позволяет найти Интеграл/, который приводит к равенству форм (28) Я = — ой-ой Где a-
не-1 constant. In факт, (28) является уравнением/. /—4-с Применение интеграции с помощью partit естественно назвать этот случай «сведением интеграции к себе».Образцы. 1) I ^ Vx ^ + многомерные выражения. Поставь xdx В XI — \ — м-н дю = ЧХ * + м’dx = ДВ, в-Х И затем… (28а) Жесткий диск Джей радиостанции VX * + м 3В ^ +
М Г Т Дж / х ’ + м Следовательно, из(28а) 1 = xYx * + м -/ + / n1n(* + г * * + / п)+ C. Таким образом… Наконец. 2) л = \ е * в COS xdx. Поставь е * = у, ду = е * ДХ, потому что xdx = ТГВ в = грех йк И затем… Дж = 6х грех дж-дж е * Sin х dх. (29) Справа вы получите Интеграл почти такой же сложности, как и оригинал. Это часто указывает на возможность
приведения интеграла к itself. In в этом случае интеграция деталей применяется к интеграции / * = ^ е * грех xdx. Похлопывание ех = у, ду = ех ДХ, грех xdx = ДВ, где V = — cosx、 Мы получаем Я * =е * Кос х-}-J В Е * потому что xdx =-е * соѕ х + /•(30), если это значение необходимо
присвоить (29)、 / = ТФ * sinx-Ф * Е * соѕ х — /、 Откуда / = г(sinx + коза:) + с (31) Заметим, что интеграл f *также был вычислен, поскольку он продолжается из (30) и (31). = г (Син х-Кос х) — ж-З. n°9.An Интеграл, который не выражен, является фундаментальным. Существует уже достаточно широкий спектр методов интеграции. Но ни один из этих методов не может найти интеграции. Я = \ х \ gxdx. (32) Кроме того, заранее можно сказать, что дальнейшее развитие техники
интегрирования не позволяет найти Интеграл (32).В связи с этим пессимистичным утверждением необходимо описать некоторые детали. Философия диалектического материализма говорит нам, что мир принципиально узнаваем. То, что не известно сегодня, будет известно позже, и невозможно ставить препятствия в развитии
нашего знания. Противоположное, антимарксистское учение, называемое агностическим, которое устанавливает некоторые ограничения на познание, опровергается развитием науки. Например, философ 19 века О. Конт сказал, что люди никогда не знают химического состава звезд. Вскоре после этого был
разработан метод спектрального анализа, который позволил очень точно изучить химическое строение входов, а гелиевые элементы были обнаружены на солнце раньше, чем на земле. В настоящее время этот элемент широко используется в технике. Существует естественное опасение, что наше утверждение о том, что интеграл (32) никогда не будет найден, не является врожденной ошибкой
агностицизма. На самом деле это не так. Мы часто выносим некоторые реальные суждения в форме противоречивых суждений. Например, хорошо известно, что сумма углов треугольника ( * ) равна 180°.Эту истину едва ли можно выразить словамиВ следующем» пессимистическом «формате:» люди никогда не научатся строить треугольник с суммой углов, отличной от 180 градусов.»Основываясь на своем знании, что сумма углов треугольника равна 180°(не зная этой истины, он не мог сделать собственного утверждения
о невозможности построения упомянутого треугольника). Теперь давайте выясним, в чем причина утверждения, что интеграл (32) никогда не найден. Во-первых, рождается идея, что»нет функции, для которой JC tg lg является производной», но эта идея неверна. Ведь функции xtgx нет. А потом она Например, прерывистый Существует примитив для этого интервала. Поэтому, есть примитивы, но они не нашли. В чем же проблема? Дело здесь в том, что нам нужно
уточнить значение слова «найти».Примеры помогут понять следующее. Представьте себе, что люди не догадались ввести тригонометрические функции. Теорема о том, что предел суммы равен сумме границ членов, не требует тригонометрии. Производная как предел отношения^знания также не нужна
х я Тригонометрия.)*Формулы, такие как, в результате развития»плохой» математики икс (ДК * г = 2dg、 Следовательно, эквивалентное выражение ^ 2xdx = х * + КТ ^%= 1 пиксель + с Поэтому в этой математике, как и у нас, возникает проблема вычисления интеграла. Конечно, расчет интеграла Джей потому xdx Нет никаких сомнений, потому что этот Интеграл был бы бессмысленной комбинацией значков.*) Однако (в этом суть Из нашего примера! Даже в «плохой математике» мы можем поставить вопрос
о нахождении интеграла (33) Для компиляции функции не требуется 3 части информации Gonoometry. At в то же время невозможно найти этот Интеграл в математике, в которой отсутствует тригонометрия. ^ q ^ = = arctgx + C Вопрос о том, является ли тот или иной Интеграл «найденным» или «не найденным», имеет другое значение в зависимости от того, какую функцию вы хотите
использовать для записи answer. In современная математика выбирает определенный набор простых функций (выше он называется элементарными функциями), и через эти функции мы пытаемся выразить интегралы, которые мы encounter. So утверждение, что интеграл (32) не найден, точнее, означает, что он не может быть выражен с точки зрения основной функции. 32) может быть
«доступен для поиска«.Вы не можете предсказать, будет ли (или как) класс базовой функции расширяться в будущем. Вообще говоря, обратите внимание, что расширение класса базовой функции не очень перспективно. Возвращаясь к примеру «математики без тригонометрии», можно сказать, что в этой математике Интеграл (33) является принятой функцией(в ней! Вы можете
видеть, что он не представлен a) Elements. It это интеграл (33), но Интеграл (32) (это была не»плохая«математика! Вам нужно еще больше расширить запас базовой функции. В заключение мы покажем некоторые интегралы, которые не являются элементарными).Это СФИ. Дж^ «*» \ e — * * dx, J sin xChx, J cos x * dx,+ 1 dx, J Vsin xdx,
Jlnsinxrfx. In в книге, о которой идет речь, само собой разумеется, что такого интеграла нет * ) Найдено. Однако в инженерной практике они встречаются очень часто. В главе о конкретном Интеграле показано, как это работает, если конкретная проблема приводит к»интегралу» без сдвига.
Смотрите также:
| Параметрическое задание кривой | Интегрирование рациональных функций |
| Кривизна | Интегрирование некоторых иррациональностей |
