Оглавление:
Множеством комплексных чисел мы называем множество выражений вида 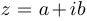 , где
, где 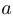 и
и 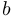 — обычные (вещественные) числа, а
— обычные (вещественные) числа, а 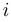 — символ, называемый мнимой единицей. При этом считается, что
— символ, называемый мнимой единицей. При этом считается, что 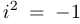 . Поэтому иногда пишут:
. Поэтому иногда пишут: 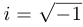 .
.
Два комплексных числа 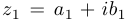 и
и 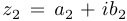 считаются равными, если
считаются равными, если 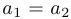 и
и 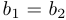 . Если
. Если 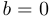 , то число
, то число 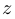 является вещественным и равным
является вещественным и равным 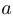 , а если
, а если 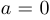 , то оно называется чисто мнимым. При этом:
, то оно называется чисто мнимым. При этом:
- вещественной частью числа
 называется число
называется число 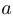 :
: 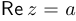 ;
; - мнимой частью числа
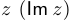 называется число
называется число 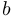 :
: 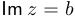 ;
; - модулем числа
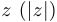 называется число
называется число 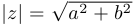 ;
; - сопряженным к числу
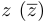 называется число
называется число 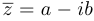 .
.
Комплексные числа подчиняются обычным правилам работы с числами и буквенными выражениями (свойствам коммутативности, ассоциативности и дистрибутивности). В частности,
1) 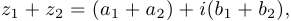
2) 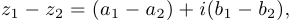
3) 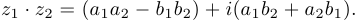
4) заметим, что 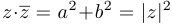 , следовательно, если
, следовательно, если 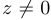 и
и 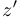 определить как дробь
определить как дробь 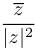 , то оказывается, что
, то оказывается, что 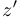 — число, обратное к
— число, обратное к 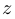 , то есть
, то есть 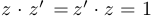 . Таким образом, если
. Таким образом, если 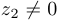 , то
, то
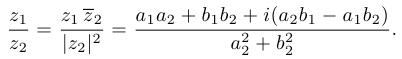
Упр. 1 Проверьте, что 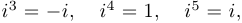
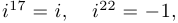
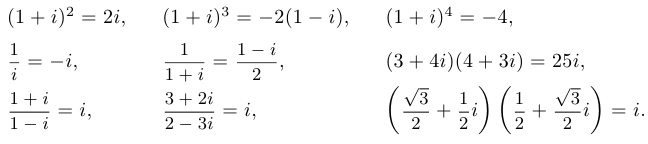
Пример 1.
Вычислить 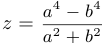 , если
, если 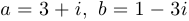 .
.
Решение. Вычислим знаменатель дроби: 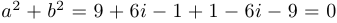 . Следовательно, число
. Следовательно, число 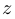 не определено.
не определено.
Пример 2.
Вычислить 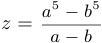 , если
, если 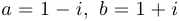 .
.
Решение. Возведем сначала в квадрат: 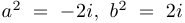 . Таким образом,
. Таким образом, 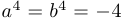 . Подставляя в выражение для
. Подставляя в выражение для 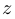 , получим
, получим 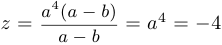 .
.
Упр. 2. Вычислите 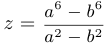 , если
, если 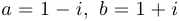 .
.
Пример 3.
Вычислить 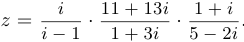
Решение. 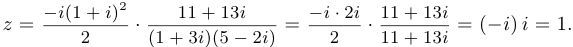
Геометрическое представление комплексных чисел.
Поскольку комплексное число 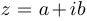 определяется парой вещественных
определяется парой вещественных 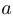 и
и 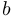 , естественно представить это число как вектор с координатами
, естественно представить это число как вектор с координатами 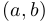 на декартовой плоскости, которую обычно называют комплексной плоскостью. Ось абсцисс на ней будем обозначать буквами
на декартовой плоскости, которую обычно называют комплексной плоскостью. Ось абсцисс на ней будем обозначать буквами 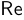 , а ось ординат —
, а ось ординат —  . Длина
. Длина 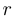 вектора
вектора 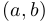 равна
равна 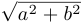 , то есть модулю числа
, то есть модулю числа 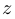 , а угол между положительным направлением оси
, а угол между положительным направлением оси 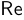 и вектором
и вектором 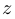 , отсчитываемый в положительном направлении, то есть против часовой стрелки, называется аргументом числа
, отсчитываемый в положительном направлении, то есть против часовой стрелки, называется аргументом числа 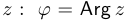 . При этом если угол находится в промежутке
. При этом если угол находится в промежутке 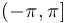 , то он называется главным значением аргумента и обозначается
, то он называется главным значением аргумента и обозначается 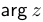 .
.
Заметим, что из неравенства треугольника следует, что для произвольных комплексных чисел 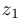 и
и 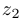 выполняется неравенство
выполняется неравенство
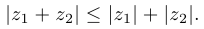
Упр. 3. Изобразите на комплексной плоскости числа 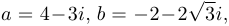
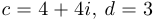 .
.
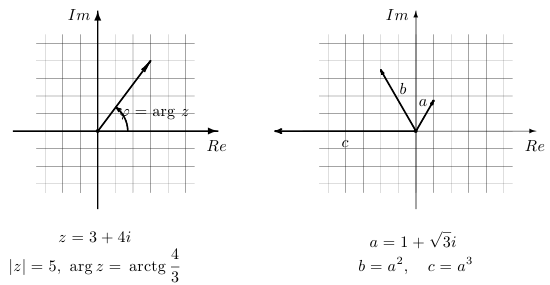
Пример 4.
Изобразить на комплексной плоскости числа 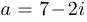 и
и 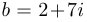 и вычислить
и вычислить 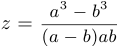 .
.
Решение. Имеем, что 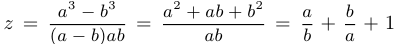 . Далее,
. Далее, 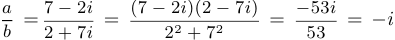 . Таким образом,
. Таким образом, 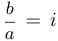 и, следовательно,
и, следовательно, 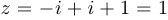 .
.
Упр. 4. Изобразите на комплексной плоскости числа 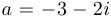 и
и 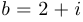 и вычислите
и вычислите 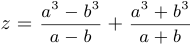 .
.
Тригонометрическая форма записи комплексных чисел.
Непосредственно из геометрического представления комплексного числа 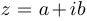 следует, что
следует, что 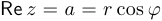 и
и 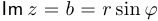 , то есть
, то есть
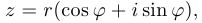
где 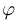 — аргумент числа
— аргумент числа 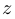 . Если учесть, что аргумент определяется с точностью до
. Если учесть, что аргумент определяется с точностью до 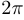 , то получим тригонометрическое представление комплексного числа в обобщенной форме:
, то получим тригонометрическое представление комплексного числа в обобщенной форме:
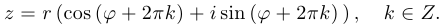
Если 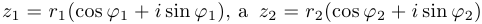 , то
, то
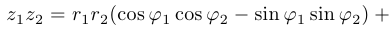
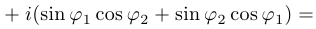
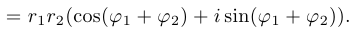
Таким образом, 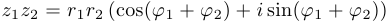 .
.
Аналогично: 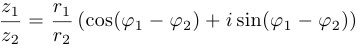 .
.
Из формулы для произведения комплексных чисел получаем знаменитую формулу Муавра:
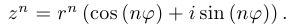
Определяя корень степени 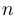 как действие, обратное возведению в степень
как действие, обратное возведению в степень 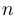 , получим формулу
, получим формулу
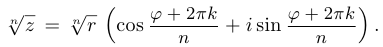
Здесь 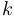 — любое целое число, однако различными эти выражения будут лишь для
— любое целое число, однако различными эти выражения будут лишь для 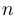 значений числа
значений числа 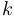 . Обычно рассматриваются
. Обычно рассматриваются 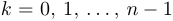 . Если мы захотим подчеркнуть зависимость корня от числа
. Если мы захотим подчеркнуть зависимость корня от числа 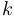 , то будем писать
, то будем писать 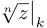 или использовать обозначение
или использовать обозначение 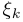 .
.
Пример 5.
Найти корни уравнения 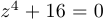 .
.
Решение. Имеем, что 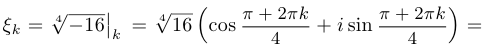
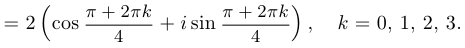
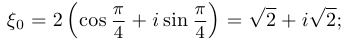
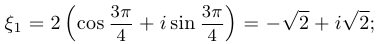
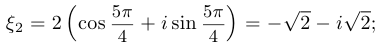
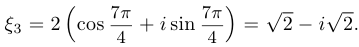
На этой странице найдёте другие готовые курсовые работы во высшей математике:
Много готовых курсовых работ по высшей математике
Можете посмотреть другие готовые курсовые работы по высшей математике:
