Оглавление:
Матрицей мы называем прямоугольную таблицу чисел. Если в матрице 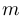 строк и
строк и 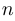 столбцов, то говорят, что матрица имеет размер
столбцов, то говорят, что матрица имеет размер  . При этом для матрицы
. При этом для матрицы

используются также следующие обозначения:
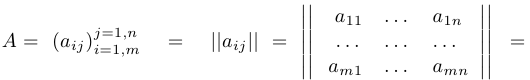

Отметим, что матрицы можно умножать на числа, матрицы одного размера можно складывать. Например:
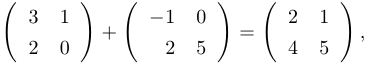
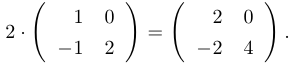
Матрица, у которой число строк совпадает с числом столбцов, называется квадратной.
Матрица, у которой только одна строка и несколько столбцов, называется вектор-строкой, или просто строкой. Матрица, у которой только один столбец и несколько строк, называется вектор-столбцом, или просто столбцом. И вектор-столбец, и вектор-строка называются также просто векторами.
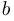 — вектор-строка:
— вектор-строка: 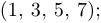
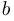 — вектор-столбец:
— вектор-столбец:  .
.
Зачастую нам не важно, в каком виде записан вектор, — как столбец или как строка. Чаще мы будем записывать вектор в виде строки — из соображений экономии места. Однако в одном случае принято писать вектор в виде столбца, если, как говорят, матрица действует на вектор. В этом случае матрица должна иметь столько столбцов, какова размерность вектора. Говорят также, что матрица умножается слева на вектор, или что вектор умножается справа на матрицу. При таком умножении в результате получается вновь вектор-столбец, но уже другого размера (если только матрица не была квадратной). Например:
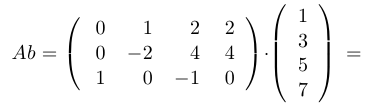

При этом матрица 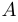 может быть вектор-строкой. В этом случае образуется вектор размерности 1, то есть просто число, которое называется скалярным произведением соответствующих векторов и обозначается через
может быть вектор-строкой. В этом случае образуется вектор размерности 1, то есть просто число, которое называется скалярным произведением соответствующих векторов и обозначается через 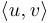 или
или 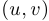 , где
, где 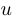 и
и 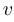 — векторы одного размера. Например, если
— векторы одного размера. Например, если 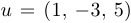 ,
, 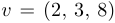 , то
, то
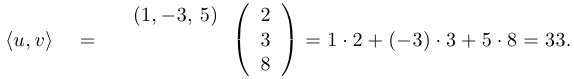
Перемножение матриц.
Если перемножаются матрицы 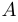 и
и 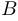 , причем матрица
, причем матрица 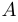 стоит слева, а матрица
стоит слева, а матрица 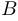 — справа, то результатом будет матрица, столбцы которой получаются поочередным умножением столбцов матрицы
— справа, то результатом будет матрица, столбцы которой получаются поочередным умножением столбцов матрицы 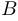 справа на матрицу
справа на матрицу 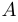 .
.
Пример 1.
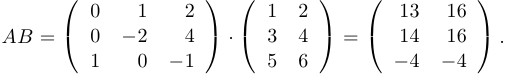
Упр. 1. Найти произведение 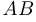 , если
, если  ,
,  .
.
Произведение матриц в общем случае не обладает свойством коммутативности (перестановочности). Например:
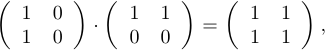 но
но 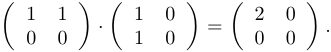
Однако операция перемножения матриц обладает свойством ассоциативности, то есть 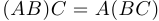 , если, конечно, произведения определены. Вместе с операцией сложения она обладает свойством дистрибутивности:
, если, конечно, произведения определены. Вместе с операцией сложения она обладает свойством дистрибутивности: 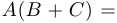
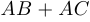 .
.
Достаточно часто приходится иметь дело с квадратными матрицами одной и той же размерности 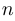 . Множество таких матриц обозначим через
. Множество таких матриц обозначим через  . В этом классе матриц существует «единица», или единичная матрица, то есть такая матрица
. В этом классе матриц существует «единица», или единичная матрица, то есть такая матрица  , что никакая матрица не меняется при умножении на нее. Это означает, что для любой матрицы
, что никакая матрица не меняется при умножении на нее. Это означает, что для любой матрицы 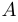 из класса
из класса  верно, что
верно, что 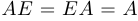 . Если хотят подчеркнуть, что матрица
. Если хотят подчеркнуть, что матрица 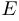 имеет размерность
имеет размерность 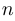 , то пишут
, то пишут 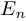 . Единичная матрица имеет единицы на главной диагонали и нули вне этой диагонали. Например:
. Единичная матрица имеет единицы на главной диагонали и нули вне этой диагонали. Например:
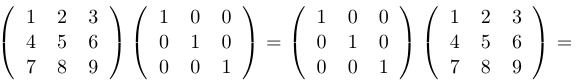
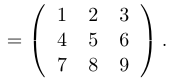
Определитель квадратной матрицы.
Важной характеристикой квадратных матриц является числовая величина, называемая определителем, или детерминантом, матрицы.
Определитель обозначается следующим образом:
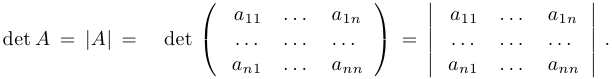
При 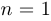 и
и 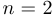 определитель задается простыми явными формулами
определитель задается простыми явными формулами
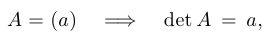

При  детерминант удобнее определить (и вычислять) «индуктивным способом» (индукция по размерности матриц). Однако прежде обозначим те аксиомы, которым должны удовлетворять определители.
детерминант удобнее определить (и вычислять) «индуктивным способом» (индукция по размерности матриц). Однако прежде обозначим те аксиомы, которым должны удовлетворять определители.
Свойства определителя:
- При перемене строк местами определитель меняет знак.
- При умножении одной из строк на число определитель умножается на это число.
- При прибавлении к одной из строк линейной комбинации нескольких других определитель не меняется.
- Определитель равен нулю, если две строки одинаковы или одна из строк состоит из нулей.
- Все указанные выше свойства верны и для столбцов.
Пример 2.
Показать, что определитель  равен нулю.
равен нулю.
Решение:
Вычтем из третьей строки вторую, а затем из второй — первую. Получим определитель  , у которого две строки одинаковы, и, следовательно, он равен нулю.
, у которого две строки одинаковы, и, следовательно, он равен нулю.
Для того чтобы осуществить индуктивный переход, то есть чтобы для подсчета определителей данного порядка использовать определители меньшего порядка, введем еще несколько понятий.
Минор.
Если после вычеркивания одного или нескольких столбцов и одной или нескольких строк в прямоугольной матрице образуется квадратная матрица, то ее определитель называется минором. Иногда минором будем называть также и саму образовавшуюся матрицу.
Индекс (знак) элемента.
Каждому элементу 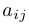 матрицы приписывается индекс — множитель вида
матрицы приписывается индекс — множитель вида  . Например, для матрицы размера 3×3 распределение знаков-индексов выглядит следующим образом:
. Например, для матрицы размера 3×3 распределение знаков-индексов выглядит следующим образом:
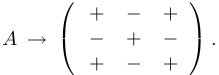
Алгебраическое дополнение.
Зафиксируем некоторый элемент 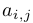 квадратной матрицы. Если вычеркнуть столбец и строку, на которых он стоит, то останется матрица, порядок (количество строк и столбцов) которой на 1 меньше. Ее определитель, умноженный на знак-индекс данного элемента, называется алгебраическим дополнением и обозначается через
квадратной матрицы. Если вычеркнуть столбец и строку, на которых он стоит, то останется матрица, порядок (количество строк и столбцов) которой на 1 меньше. Ее определитель, умноженный на знак-индекс данного элемента, называется алгебраическим дополнением и обозначается через 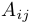 . Например:
. Например:
если 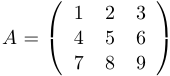 , то
, то 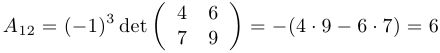 ;
; 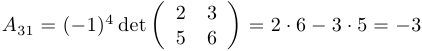 .
.
Правило Лапласа разложения по элементам одной строки (столбца).
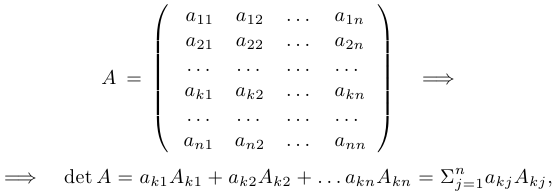
где 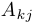 — алгебраическое дополнение к элементам
— алгебраическое дополнение к элементам 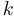 -й строки.
-й строки.
Пример 3.
Найти определитель матрицы  .
.
Решение:
Разложим определитель по элементам, например, 1-й строки:
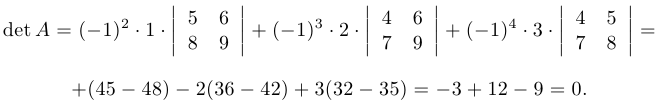
На этой странице найдёте другие готовые курсовые работы во высшей математике:
Много готовых курсовых работ по высшей математике
Можете посмотреть другие готовые курсовые работы по высшей математике:
| Курсовая работа на тему: графики функций |
| Курсовая работа на тему: кривые, заданные параметрически |
| Курсовая работа на тему: системы линейных уравнений |
| Курсовая работа на тему: комплексные числа |
