Оглавление:
Достаточно часто кривые задаются в параметрическом виде: 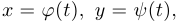
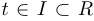 . Например:
. Например: 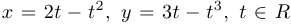 . Функции
. Функции 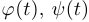 называются координатными функциями.
называются координатными функциями.
Для того чтобы изобразить такую кривую, рекомендуется следующая программа:
Шаг 1. Проводим исследование координатных функций 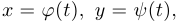
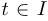 и строим их графики.
и строим их графики.
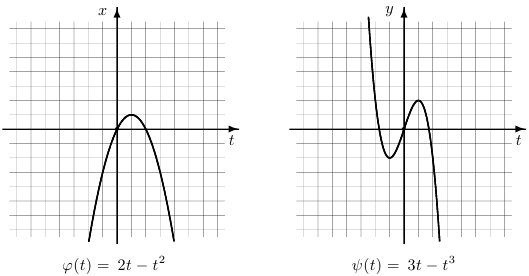
Шаг 2. Рассматриваем критические точки координатных функций, то есть такие точки кривой, в которых производная одной из координатных функций равна нулю. В нашем примере 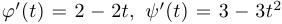 и, следовательно, таких точек две:
и, следовательно, таких точек две: 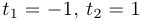 .
.
Особыми точками будем называть точки, в которых обе производные обращаются в нуль или не существуют. Остальные точки называются регулярными.
В нашем примере особой является точка, соответствующая 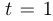 . В особой точке касательная к кривой не всегда определена. В регулярной точке касательная определяется следующим образом: считаем тангенс угла
. В особой точке касательная к кривой не всегда определена. В регулярной точке касательная определяется следующим образом: считаем тангенс угла 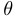 наклона касательной к положительному направлению оси абсцисс (аналог производной
наклона касательной к положительному направлению оси абсцисс (аналог производной 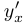 ) по формуле
) по формуле
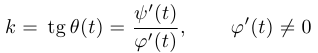
и тем самым определяем тангенс угла наклона касательной к графику в не особых точках. Если 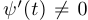 , а
, а 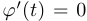 , то касательная к кривой будет вертикальной.
, то касательная к кривой будет вертикальной.

Шаг 3. Отмечаем на прямой 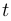 критические точки координатных функций (а также точки разрыва производной каждой из координатных функций).
критические точки координатных функций (а также точки разрыва производной каждой из координатных функций).
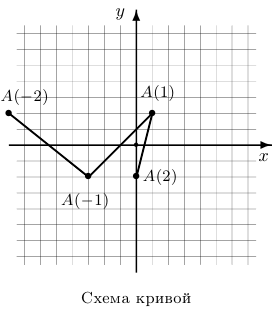
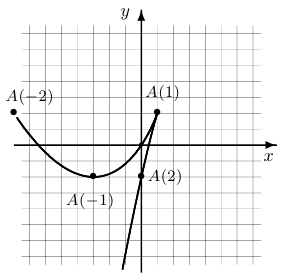
Шаг 4. Фиксируем на плоскости 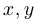 все отмеченные точки и соединяем их между собой отрезками вместе с указанием на направление изменения параметра
все отмеченные точки и соединяем их между собой отрезками вместе с указанием на направление изменения параметра 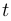 . Получим схему кривой. Для того чтобы понять направление кривой при приближении к границе области задания (в частности, при
. Получим схему кривой. Для того чтобы понять направление кривой при приближении к границе области задания (в частности, при 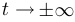 ), нужно найти пределы
), нужно найти пределы
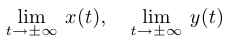
или подсчитать значения в одной из точек, близкой к границе.
Шаг 5. Считаем производную 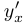 по формуле
по формуле
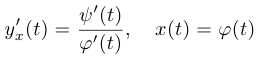
в точках, где 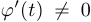 , и тем самым определяем тангенс угла наклона касательной к графику в регулярных точках. Подставив несколько контрольных значений, окончательно уточняем график.
, и тем самым определяем тангенс угла наклона касательной к графику в регулярных точках. Подставив несколько контрольных значений, окончательно уточняем график.
Поведение кривых в особых точках.
На представленном ниже рисунке показаны возможные типы поведения кривых вблизи особых точек. Везде в качестве особой точки рассматривается начало координат. Кривые задаются следующими координатными функциями:
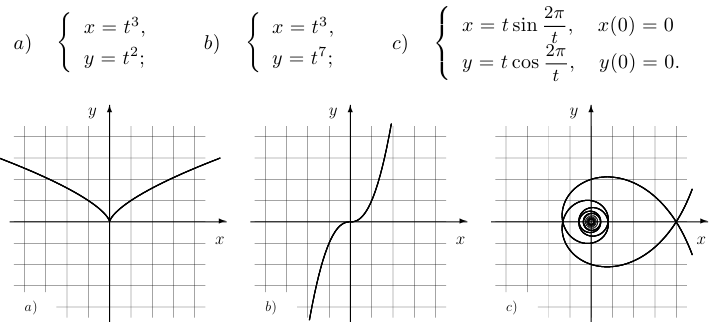
Параметрически заданные кривые иногда называют траекториями, интерпретируя параметр 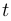 как время.
как время.
Пример 1.
Траектория точки на окружности, катящейся по прямой без скольжения, называется циклоидой.
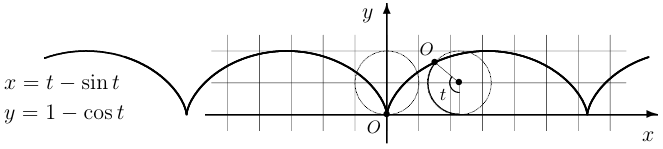
Кривые в полярных координатах.
Достаточно распространенным является использование в качестве параметра полярного угла, то есть угла, который отсчитывается от луча 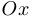 до направления на точку против часовой стрелки. Говорят, что кривая задана в полярных координатах, если задан полярный радиус
до направления на точку против часовой стрелки. Говорят, что кривая задана в полярных координатах, если задан полярный радиус 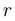 (расстояние от начала координат до точки) как функция полярного угла:
(расстояние от начала координат до точки) как функция полярного угла: 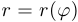 . Функция
. Функция 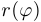 при этом обычно предполагается периодической с периодом
при этом обычно предполагается периодической с периодом 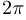 . К декартовым координатам можно переходить по формулам
. К декартовым координатам можно переходить по формулам

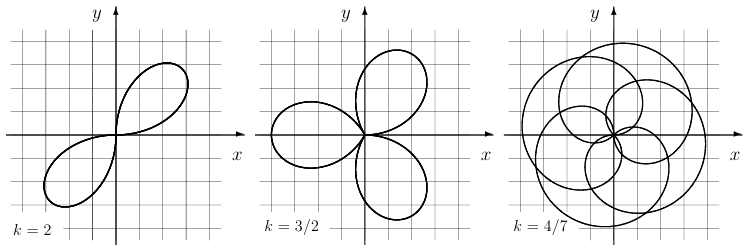
Полярной розой называется кривая на плоскости, уравнение которой в полярных координатах имеет вид 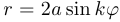 , где
, где 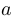 и
и 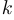 — некоторые постоянные. На рисунке ниже изображены три таких кривых, построенных при
— некоторые постоянные. На рисунке ниже изображены три таких кривых, построенных при 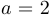 и различных
и различных 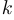 .
.
Пример 2.
Показать, что роза, соответствующая 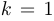 , является окружностью радиуса
, является окружностью радиуса 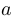 с центром в точке
с центром в точке 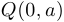 .
.
Решение. Рассмотрим произвольную точку 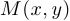 на кривой, где
на кривой, где 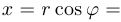
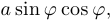
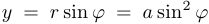 . Тогда
. Тогда 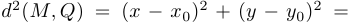
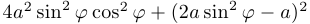
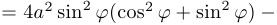
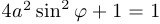 . Утверждение доказано.
. Утверждение доказано.
Степенной розой называется кривая на плоскости, уравнение которой в полярных координатах имеет вид 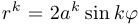 , причем независимо от
, причем независимо от 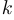 угол
угол 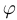 таков, что
таков, что 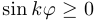 .
.
Лемнискатой относительно фокусов 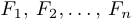 называется множество точек
называется множество точек 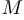 таких, что произведение расстояний от
таких, что произведение расстояний от 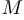 до фокусов постоянно. Лемниската называется центрально-симметричной, если фокусы образуют правильный
до фокусов постоянно. Лемниската называется центрально-симметричной, если фокусы образуют правильный 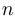 -угольник с центром в начале координат и само начало координат входит в это множество.
-угольник с центром в начале координат и само начало координат входит в это множество.
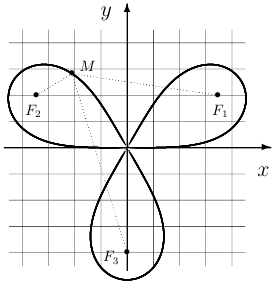
Упр. 1 Покажите, что степенная роза, соответствующая 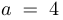 и
и 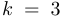 , изображенная на рисунке справа, является лемнискатой относительно фокусов
, изображенная на рисунке справа, является лемнискатой относительно фокусов 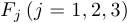 с координатами
с координатами 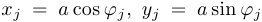 , где
, где 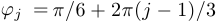 .
.
Упр. 2 Покажите, что роза степени 2 также является центрально-симметричной лемнискатой (она называется лемнискатой Бернулли). Постройте ее и найдите ее фокусы.
Параметризация кривых, заданных неявно.
Говорят, что кривая на плоскости задана неявно, или в неявном виде, если координаты ее точек определяются уравнением 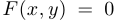 . Например:
. Например: 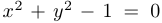 — уравнение окружности. В этом случае, предполагая, что кривую на нужном участке можно задать равенством
— уравнение окружности. В этом случае, предполагая, что кривую на нужном участке можно задать равенством 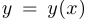 , где
, где 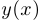 — функция, имеющая производную, получим для функции
— функция, имеющая производную, получим для функции 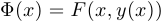 :
:
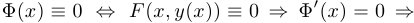
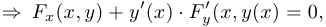
откуда определяется производная 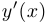 .
.
Попытки разрешить уравнение 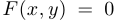 относительно
относительно 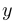 редко приводят к удобному способу изображать кривую. Например, даже в случае окружности мы получаем не слишком хорошую зависимость:
редко приводят к удобному способу изображать кривую. Например, даже в случае окружности мы получаем не слишком хорошую зависимость: 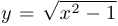 при
при 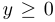 и
и 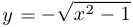 при
при 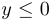 .
.
Другой, более предпочтительный способ изображения кривой состоит в том, чтобы представить ее в параметрическом виде. Переход от неявного задания кривой к параметрическому и называется параметризацией.
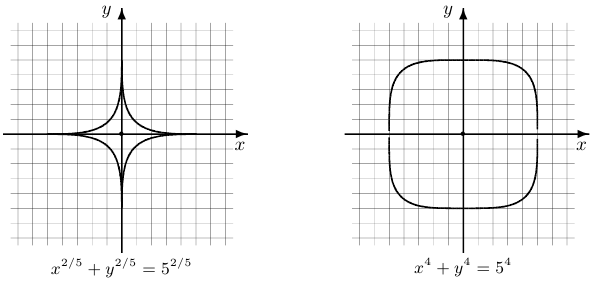
Пример 3.
Астроида 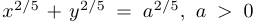 , допускает параметризацию
, допускает параметризацию 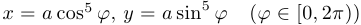 .
.
На этой странице найдёте другие готовые курсовые работы во высшей математике:
Много готовых курсовых работ по высшей математике
Можете посмотреть другие готовые курсовые работы по высшей математике:
| Курсовая работа на тему: правило Лопиталя и выпуклость |
| Курсовая работа на тему: графики функций |
| Курсовая работа на тему: матрицы и операции с ними |
| Курсовая работа на тему: системы линейных уравнений |
