Линейные отображения: определение, примеры

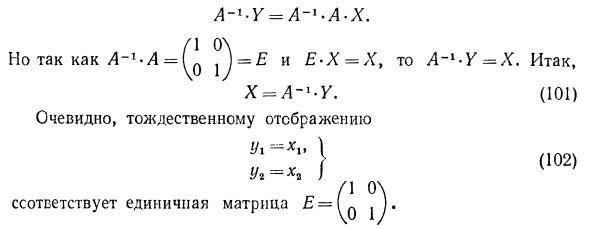
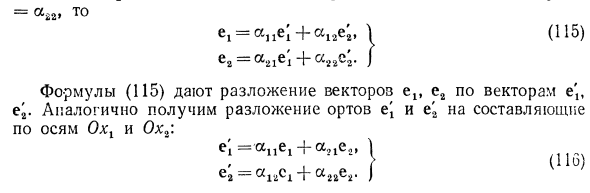
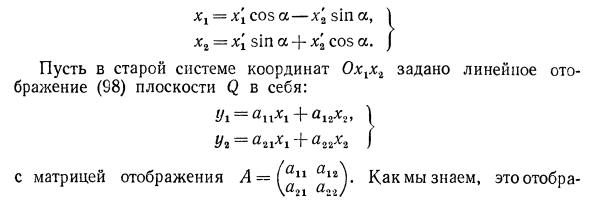
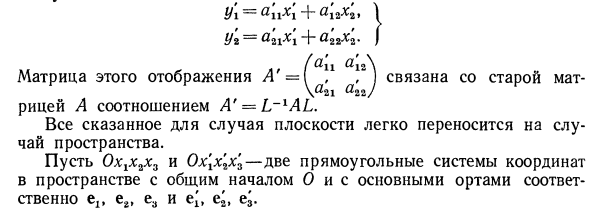
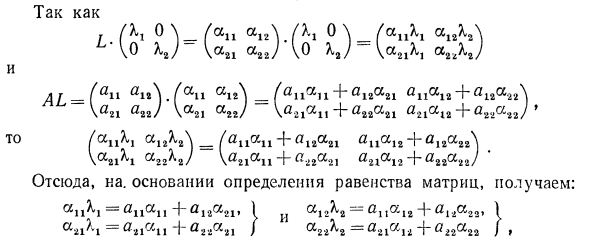
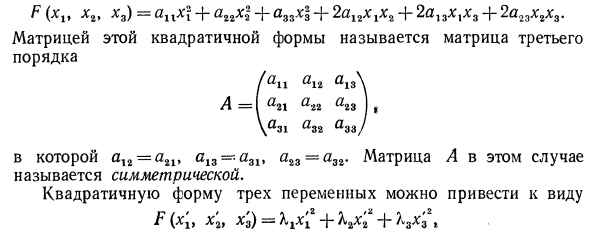
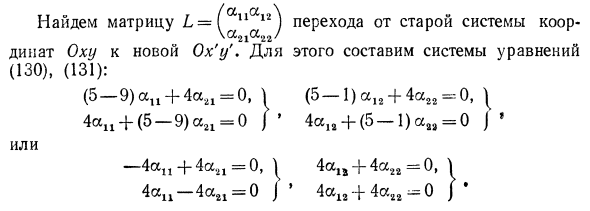
Линейные отображения

• ЛИНЕЙНЫЕ ОТОБРАЖЕНИЯ /. Основные понятия Пусть в плоскости Q задана прямоугольная система координат. Для упрощения записи и удобства преобразования координаты точек будем обозначать не через х и у, а через хх и хг или ух и уг и т. Д., А основные орты вместо я и J через е, и е2. Рассмотрим уравнения, связывающие переменные ухо и у2: (98) где alt9 avl> a.n, а2., — постоянные. Каждая точка М плоскость Q с координатами х1 и х2 соответствует в этом же плоскости единственной точки Мг координаты которой ух и у2 определяется соотношения (98). М. точка, называется образом точки М.

. Как говорят, с помощью уравнений (98) устанавливается отображение или преобразование плоскости Q в себя. В связи с тем, что правой частями уравнений (98) первая степень относительно х1 и хга этого отображения называется линейным. В заданной системе координаты Охая, линейное отображение вполне характеризуется квадратная матрица аи а12 составленной из коэффициентов линейного представления (98). Если ввести матрицу-столбцы X = Y = то система уравнений (98) можно записать в следующей матричной форме (см. § 4, стр. 4): У = АХ. (99)

Если точка М описывает в плоскости Q некоторую линию L, то ее образ описывает, вообще говоря, также некоторую линию L, Людмила Фирмаль

Так как е ^ е ^ л, е, -е2- = 0, е2-е2 = 1, то, что принимают во внимание формулы (115), получатель е, • ej = + а \ г = 1, е, • еа = а, хаг1 а12а22 = О, ег-е1 = аг21 + сс | 2 = 1. (117) Аналогично, так как е [• ei = 1, е [• е2 = 0, е2 • е2 = 1, то из формул (116) получим ах + <*! i = 1> апа12 — {- а21а.22 = 0, а? 2 + а | 2 = 1. (118) Иными словами, матрица L обладает следующими свойствами :.

Сумма квадратов элементов строки (или столбца) равна единице, сумма парных произведений элементов строки (столбца) на соответствующие элементы другой строки (столбца) равна нулю Матрица, обладающая этими свойствами, называется ортогональной. а11 «21 Рассмотрим транспонированную матрицу L * = [], которая \ ач а22 / составим произведение матриц L * L. ‘«П а» Л / ап ai2 \ Л ? 1 + а? 1 Ча12 <Ш Ш а22 / \ а12а11 Н ~ а22а21 + < «/ -С!) «* • (и9) Таким образом, матрица L * является обратной связью с матрицей L: L * = L ~ l.

• Решение задач по высшей математике

Системы уравнений первой степени	Плоскость
Матрицы и действия над ними	Прямая в пространстве

Примеры решения и задачи с методическими указаниями

Решение задач	Лекции
Сборник и задачник	Учебник

• Замечание. Если новая система координат получена из старой системы поворотом осей на угол а, то легко видеть, что формулы (ИЗ) аналогичны формулам поворота осей координат, рассмотренным в гл. I, § 6, п. 2. Действительно, в этом случае (см. Рис. 79) a11 = cos (eI, e1 ‘) = cosal al2 = cos (elt е2) = cos -j- a ^ = -грех, a21-cos (e2, e () = cos ^ —a) = sina, a22 = cos (e2, е2) = со $ аг и, следовательно, формулы (113) принимают вид: хх-а’и потому а — х’2 грех а, 1 хг = х [грех а-j- ^ 2 cos а. J Линейное отображение (98) плоскости Q в себя: tJi = ayxxx + беспокойство „\ с матрицей представления Л = (^ п а | 2). \ 21 «22 /

можно записать в матричной форме (99) 7 = ЛХ, Здесь Х = a Здесь (xlt х2) -координаты точки М, а . (У 1 »У *) — координаты ее образа Мх в старой системе координат Тогда по формелам (ИЗ) получим xl = беспокойство + alv £, \ == У * ч \ Ху -j- СС. ^ Хо / и аналогично У \ = а \ У \ + а12 # 2 »\ -А2 \ У [+ ^ ччУ’г Г У * / Если ввести матрицы-столбцы X ‘= (!) И Г = и матрицу преобразование L = (апа12). \ 21 22 / записать в следующей матричной форме: X = LX \ Y = LY ‘. (120) .

Пусть (х [, л; ^) -координаты точки М, а (у [, у’2) — координаты ее образа уИ, в новой системе координат Людмила Фирмаль

Найдет теперь зависимость между координатами точки М и ее образом в новой системе координат Ох \ хг Для этого подставит в уравнении (99) и выражение X Y по формулам (120): LY ‘= ALX’. (121) Матрица L «1, матрица L L. Замечательная, что L ~ l-L Y ‘= L ~ LALX’. (122) Таким образом, координаты х [, хг точки М и координаты у [, // 2 ее образа в новой системе координат Ох [х’г связаны формулой (122), которая показывает, что в новой системе координат линейное отображение плоскости Q самой в себя имеет матрицу A ‘-L «LAL.

Итак, в новой системе координат линейное отображение имеет следующий вид:Уг = а21х [+ а22х1 I (а [1 а [Л \ связано со старой матрицей. Все сказанное для случая полета легко переносится на случай пространства. Пусть Охух2хз и Ох \ х2х2-две прямоугольные системы координат в пространстве с общим началом О и с основными ортами соответственно ех, е2, е3 и е [, е *, е ^.

Положим aij = е / • е / -cos (® / Г® /) ‘(‘ = 1,2,3; / = 1,2,3). Например, an = е1е’1 = cos (elt е |), а23 = е2 • е.; = Cos (е2, е ^). Тогда аналогично предыдущему получим формулу преобразования координат: Х1 = тревога + а1Л + а13Х3 »1 = + [(123) с матрицей преобразованием / аи а12 а13 \ L = f а21 а22 а23 \ а31 а32 сс33 / Можно показать, что матрица L ортогональна, а / а21 a3i \ L * = i а12 а22 а32 j = L ~ 1. \ Ct13 сс23 а33

Если в старой системе координат Ол ^ дс ^ задано линейное отображение yl = allxl + al2x2 + al3x3, У’1 = ^ 21 * 1 И «^ 22 * ​​2 +« 23 * 3 »* / з =« 31 ^ 1 + ^ 3 гхг + а39х3 / аи а12 а13 \ с матрицей А = я а21 а22 а23), то в новой системе координат матрица \ а31 а32 я33 / линейное определение определяется формулой А ‘= L ~ lAL. 3. Приведение квадратичной формы к каноническому виду Квадратичной формой двух явлений является одинаковое многочлен второго степенного трьепина хх и х2: F (xlt х2) = а1Ух \ -f 2а12ххх2 4- а2гх (124)

Покажем, как квадратичную форму можно записать в матричной форме. F (xlt xt) = (allxl + altxt) xl + (a 21 * 1 + агчх, г) хг * полагая а21 = а1г. Матрица называется матрицей квадратичной формы.Введя матрицу-столбец X = и матрицу-версию Х * = (ххх2), легко подтвердить, что квадратичная форма (124) F (xx, x2) = X * AX. (12G) Действительно, по правилам умножения матриц постоянно находим: АХ = (аи ахЛ (хЛ_ (ах1хх + а12хА \ а2Х агг) \ xj \ а2ххх + <*% & / 9 = * 1 («11 * 1 +« 1 Л) + * 2 («21 * 1 +« 22 * ​​2) -F (* 1> * 2) « Будем трактовать переменные хх и х2 как координаты точек в прямоугольной системе координат Оххх2.

Рассмотрим новую прямоугольную систему координат Ох [х2. Пусть координаты точек в старой и новой системах связаны между собой формулами преобразования (113) х, = Ч-а11 * 1 + а12 * 2 »\ ‘г ~ а21 * 1 ~ Ь а22 * 2 Дж с ортогональной матрицей преобразования L — <^> 0РмУлы преобразование (113) можно записать в следующей матричной форме (см. п. 2): X = LX \ (127) Здесь Х = (£), Х ‘= Если вместо хх и х2 в квадратичной форме (124) подставим их выражения (113) через х \ и х2, то получатль

Поставим перед собой задачу: выбрать новую систему координат Ох [ха так, чтобы в квадратичной форме Р (х’х, х2) отсутствовал член с произведением координат, иными словами, чтобы она приняласледующий вид: F (x (t х2) = VI ‘+ (128) который называется каноническим. Мы будем проводить в матричной форме. Рассмотрим прежде всего матрицу-версию X ‘* = (x’lt х2). X * -Xr ‘L-1. (129)

Действительно, так как 1г1 = 1 * = I11). (См. П. 2В то (113) а, -f ctl2x2 ~ и -f + аi2x’2 = xt, то X ‘* L ~ l = (xl9 хг) = Х \ Подставим в правую часть равенства (126) для F (xlt х2) выражения X * и X из равенств (127) и (129): F (xlt хг) = ХМХ = (X ‘* /, — 1) Л (LX’) = X ‘* (L ~ ML) X’ = F (xlt х2). Итак, в новой системе координат матрица квадратичной формы L: Итак, матрица L преобразования удовлетворяет условию F (*;, *;) = X« (L-ML) X ‘ имеет следующий вид: А ‘= L ~ ML.

Чтобы матрица приняла следующую форму: В этом случае говорят, что матрица приведена к диагональному виду. Матрица L преобразование удовлетворена Так как (\ г 0 \ (ап а1г \ пг 0 \ _ (<х1х \ х а12 \ Л \ 0 К) V «21 a J VO KJ- \ * nK cl, JJ Аш (ап а1г \ {аи а, л (аияп + а1гаи анал2 + альза „\ \ a2i агг / \ а21 агг) \ а21аи + агга21 а.па42 + a ^ ai2J ‘ \ _ / «Цац + Яца.1 + *!« <, Л \ a2Ai anV V «2iaii + ^ 2a2i« .Л2 + аиам; ‘Отсюда, на. Основании определения р „в < ^ aua12 + aua22, 1

матрицей линейного представления 22 … Ния Линейное отображение называется невырожденным, если его матрица невырожденная, т е если \ А \ Ф0 Если же |. Л | = 0, то отображение называется вырожденным. Если линейное отображение невырожденное, то система (98) однозначно разрешима относительно хх и рамок .Матрица А называется определитель | А | = ахх аХ2 ах 42 а> ‘ми ^ , _ U2I 7 ~~ Га Г 22 \ А А У 2 « ’11 Уг- Итак, Ух а.: ’12 • п (100) х2 = — ’21 41 01 + Уг

Уравнения (100) показывает, что, обратно, каждая точка Ой (YXT у2) соответствует единственной точке / И (хЕ х2), а именно та точка М, образом которой являлось точка Ой. Таким образом, невырожденным линейным отображение определяет взаимно однозначное отображение плоскость Ормулы (100) показывают, что г Ml | Л | ’12 а.п аи К уравнению (100) также можно прийти, если умножить обе части матричного уравнения (99) на матрицу Л-1:

«11 скажи ■ = i« lAi + a2i («22- ^ 1) = 0 / a12 (au -X2) -f a22a12 = 0, 1 a12a21 + a22 (a22-A, t) »0) ‘ Таким образом, неизвестные коэффициенты преобразования ап, АВХ2 »a2i» а22 находятся из систем уравнений (130) и (131). Каждая из этих систем является однородной. Для того чтобы они имели отличные от нуля решения, необходимо и достаточно (см §. 2 , стр. 4), чтобы быть равным нулю: (131) или 12 «Ц —К а а а = 0, = 0 и а 12 «22 ^ 2 а 21 21 «** — К Таким образом, квадратные уравнения «И- ^ а. а (132) = 0 12 а22 —А, (133) 21 или Ь2 — («11 +« 22) ^ + («11« 22- «12« 2л) = 0. Дискриминант D этого квадратного уравнения всегда неотрицателен. D = (аи + а22) 2—4 (апа22 — а12а21) = а \ г -f 2ana22 + -Ь4 «12« 21 = («11—« 22) 2 + 4 «? 2» ™ К КаКЯ12 = Я21. Итак, уравнение (132) всегда имеет действительных корни.

Уравнение (132) называется характеристического уравнение матрицы Л = (а11 ai2J. Корни А,! И это уравнение называется * «21« 22 ‘ собственные значения матриц А. Подставляя найденный из уравнения (132) значения \ и в системах (130), (131) и решая их, найдет коэффициенты преобразования координат апа, а12, а21, а22.

Замечание I. Квадратичная форма трех точек зрения> х2> х3 имеет вид F (xlt x2t x3) = aixx \ -f аггх \ + a33x \ + 2а1 гххх% + 2at3xtxs + 2а23хгх 3. Матрицей этой квадратичной формы называется матрица третьего порядка А = 1 в которой аХ2 = а21> С13 = ГЙ31 »ачз ~ азг- Матрица А в этом случае называется симметрической. Квадратичную форму трех явлений можно привести к виду F (x’l9 x’it х’3) = + К2х2 + Ъ3х3 \ ап а12 а ап аи а Д31 а

где число Xlt и Х3 всегда действительны и удовлетворены ап — К «12« 13 аи «22 ^« 23 = 0. «31« 32 «33 ^ 3 а м е ч а н и е 2. Матрице А = квадратичной формы соот- линейное отображение 0i = «ii * i +« i ** i> I При переходе на новую систему координат Oxjx * с матрицей преобразований L = (^ «а») линеииое отоьо брае y’i = «п * 1 +« 1А. \ Матрица нового восприятия измерением A ‘-L ~ lAL (см. п. 2).

Если вы хотите новую систему координат, выберите форму, в которой F (хх% х’г) = ‘К1Ху -с матрица А ‘имеет вид А’ = формулы линейного преобразования (98) в системе координат Ох \ хг запишутся следующим образом: X’t> \ \ у’г-‘К% хг. \ Рассмотрим в новой системе координат Ох (х \ точки М, (1; 0), М2 (0, 1) .Очевидно, что ОМ1 = * е (и 0МгВ с о 0 Q2 (0; _A.2). Вектор OQ ^ A ^ eJ будет, соответственно, OMx = t (t вектор OQ2 = A.2e2-следовательно, 0M2-t2.

Итак, при линейном отображении (134) используются [и е2 преобразуются в соответственно коллинеарно Если при некоторой линейном отображении существует не равный нулю вектора г, образом которого является коллинеариым ему вектор Яг, то вектор г называется собственный вектор этого линейное отображение, а число Х-собственное значение отображение. Таким образом векторы е [и е2 являются собственными векторы линейного отображение (134).

Упрощение общих уравнений кривой второго порядка Вы можете упростить общее уравнение кривых Ах2 + 2 Вху + Су2 + 2 Дх + 2 Еу + F = 0. (135) Если это уравнение не содержит члена с произведением координат, т. Е. Коэффициент 2В ^ = 0, то, дополняя члены, содержащие хну, до полных квадратов, мы можем привести уравнение (135) к каноническому виду (см. Гл. II, § 2, п. 10). Пусть теперь в уравнении (135) коэффициент 2В = ^ = 0. В этом случае для приведения уравнения к виду, не содержащему члена с произведением координат, поступаем следующим образом.

Рассматривая квадратичной форма F (х, у) = Ахг + 2Ая — \ -. Су *> составленная из старших членов левой части уравнения (135), приводит ее методы, изложенная в предыдущем пункте, к сумме квадратов При этой общем уравнении кривого второго порядка (135). Общее уравнение кривой второго порядка. 5х2 + 8ху + биф-18 * -1 К + 9 = 0. Квадратичная форма, составленная из старших членов Здесь ап = 5, а12 = а21 = 4, а22 = Ъ \ матрица Д = Составляем прогнозное уравнение (132): = 0 или X2— ЮЛ, -} — 9 = 0. Корни этого уравнения XL-9, Хг = . Квадратичная форма в новой системе координат Ох’у ‘запишется, соле F (* ‘, у’) = V «+ Кл’г = 9 * » + 1 • У ‘*.

Найдем матрицу L = (11 12) \ а21а22 / дииат Оху к новой Ох’у ‘. Для этого составим системы уравнений (130), (131): (5-9) au + 4ccal = 0, \ (5-1) а12 + 4a, e = 0, \ 4аи + (5-9) 0 ^ -0 J ‘4а1в + (5-1) аи = 0] ‘ или —4а11 + 4а, 1 = 0, ^ 4alt + 4ct22 = 0, ^ 4au-4a21 = 0 J ‘4a12 + 4a22-0 J’ Первая система уравнений-это уравнение. Согласно п. 2, матрица L ортогональна. + = 1 и aj1 + a | a = l. Так же, как в то же время, ап = а41 и а22 = -а12, находим —1 1 а11 = в »1 =, -, Г7Г И а12 = —а22 ± VT 12 ± YT% 22 ± ут% знак «плюс», получим 1 _1 i 1 ~ ут9 «21» VT ‘а12 = — «» «» / Г *. Итак, формула преобразования координат Младшие члены общего уравнения кривой: -18 * -Щ + 9 = -JL (* ‘- <,’) — JL (* ‘+ уГ) + 9 = +

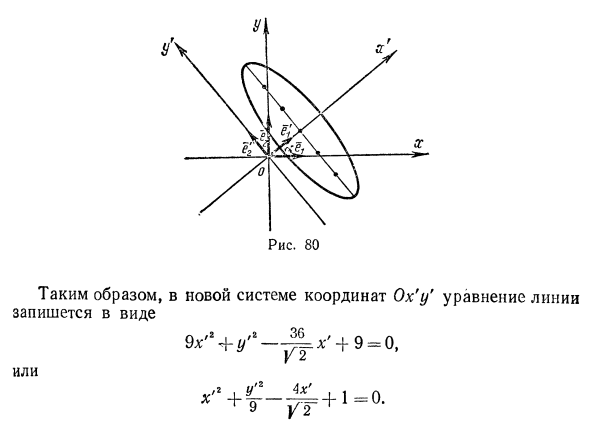
Таким образом, в новой системе координат + + 9 = 0, или 1 = 0 Вы получите в полном составе, полный квадрат, получим (х’-УТ) * 1 г 9- Таким образом, данная линия является эллипсом, центр которого в новой системе координат находится в точке 0t .. (У 2; 0) Для того чтобы установить расположение эллипса относительно старой системы координат, надо определить положение новых осей относительно старой системы

Для этого достаточно установить углы между новой системой координат и новой системой координат. Согласно формулам (112) > cos (егГе;> = ап = у =, cos (еД;) = а12 = -, cos (е2Ге!) = «я-у ~, cos (е2Ге;> = а22 = у =. Следовательно, е, Ге; = 45 °, е ^ е; = 135 °, е ^ = 45 °, е2’ег = 45 °. Расположение осей и эллипса приведено на рис. Но так как A ~ l-A = Q = £ и Е’х = х> так Итак, Х = (101) Очевидно, тождественному отображению Ух — 1 / 1 0 \ ссответствует единичная матрица £ = (q j) «

Пример 1. Линейное отображение уг = 2хг + 3х% 9 \ У г = 3 *, + Ьх2 I л (2 3 \ невырожденно, так как его матрица ^ = 5) имеет определитель 2 3 Л | = ^ 5-1 »отличный от нуля. хх = Ьух-Ъу „\ 3Л + 2ЛГ (104) f 5 —з \ Обратное отображение имеет матрицу Л_1 = 1 ^ 2) • Образом точки М (1; 2) будет точка М1 с координатами # 1—2 * 1 4-3-2-8, * / 2 = 3 • 1 — {- 5 • 2 = 13. Образом прямой L хх + х 2 = 0 будет прямая Llt уравнение, которое получит, если в уравнении хх -f 2xz-2 = 0 подставим выражения и + Зу1 + 2уг) —2 = 0 или —У \ — \ ~ Уг — 2 = 0.

Пример 2. Линейное отображение г / 1-2хх + Зх2,) У г = 4 *, + 6 * 2 | л (2 л вырожденное, так как матрица г) имеет определитель 2 3 равный нулю. Л 1 = 4 6 . И не устанавливаешь взаимно однозначное отображение плоскости в себя Действительно, из соотношения (105) легко видеть, что любая точка М прямой 2ли:, Зхг = 0 имеет своим образ начаты координаты, так как ух = 2ое -} — Зл: 2 = 0 и yz = 4хг -j- 6л: 2 = 2 (2хх -f Зх2) = = 2-0 = 0. Пример 3, Линейное отображение (105)

(106) У ‘<= * -Х 2 Дж с матрицей . Невырожденное и представляет собой отображение, при котором образом каждой точки М (xlfxt) является точка Mv симметричная относительно оси Ох, (зеркальное отображение) Так, например, образом точки М (1; 2) будет согласно уравнениям (106) точка AFJ (л ; —2). Рассмотрим радиус-вектор ОМ точки М (ху, хг): = л ОМ :. 1е1 + хге2 Отображение (98) ставит в соответствие этому радиус-вектору радиус-вектор О Му точки Мр являющейся образом точки М: при этом проекции этих векторов xlt х2 и ylt связаны формлами (98).

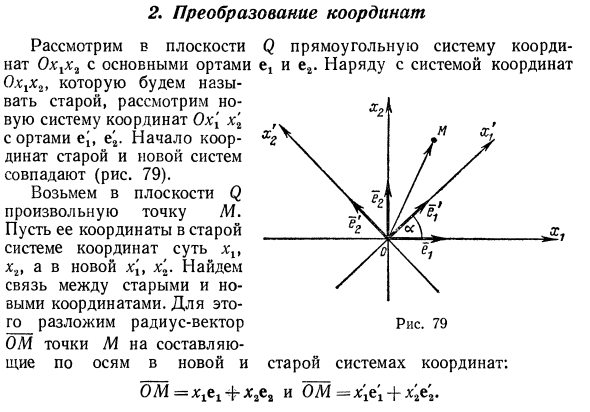
В заключение отметим, что в случае пространства невырожден- (107) с матрицей Если отображение называется не рожденным. Введя матрицы-столбцы равным образом получаются следующие два матричных уравнения, аналогичные уравнения (99) и (101):Преобразование координат Рассмотрим в плоскости Q прямоугольную систему координат Оххх9 с основными ортами и е2 и др. Наряду с системой координат Оххх2, которую будем называть старой, рассмотрим новую систему координат Ох [х’г с ортами е [, е ^. Начало координат старой и новой систем встречаются (рис. 79).

Возьмем в плоскость Q Пусть ее координаты в старой ej Рис. 79 .. Системе координат суть хи хг, а в новой х [т х’2 Найдем связь между старыми и новыми координатами Для этого разложим радиус-вектор ОМ точки М на составляющие по осям в новой и старой системах координат: ОМ = хгег -ф- дг2е2 и ОМ = * iei + * 2е’2. Таким образом, * ici + х., е.г = х (е \ И- хлг. (109) Умножим обе части равенства (109) принимаем во внимание, что e1-ef = 1 и е, -е2 = 0, получим xi = х \ (ех • нет) + х’г (et • е;>. (110)

Умножая обе части равенства (109) скалярно на е2, получим аналогично Х% = х \ (<V ■ el) + (ег • e-i). (111) Введем обозначения: «П = ei ‘e’i-lei I • I eC cos (е„ ej) = cos (elf e’,), | ai2 = ei ‘ei-cos (eiTci) f (112) / * Ч / 4 a2i-e2 * e’i-cos (e2, el), a22-e2 • e2 = cos (e2, e2). Тогда уравнения (110) и (111) запишутся в виде: Х \ = ail * t + ai «* 2» \ Xt = 1 до «« 2 2Х2 ‘) (113) Формулы (113) «11« 12 L = [11 «(И4) ^ «21« 22 / называется матрицей преобразования. fx Д fx [\ Рассмотрим матрицы-столбцы X ^ I) и X ‘= I ^]. \ А’г / \ хг / образование координат (ИЗ) в матричной форме запишется в виде X = LX ‘. Устанавливает некоторые свойства матрицы. Так как npe’et = cos (et, е [) = ау, np ^ e ^ a ^, пре’ег ^ = а21, пр ^ е., ^ X 2 1 2 = а22, то е ^ а ^ + а ^ е;, \ (115) е2 = а21е; + а22с;. J Формулы (115) дают разложение векторов от е2 до векторов е ‘„е2. е1 a- «iiei + o6, le1, | е2 ==« 12сА + а22ег J