Оглавление:





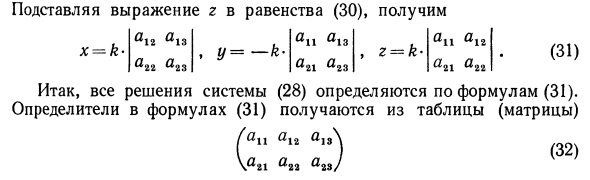

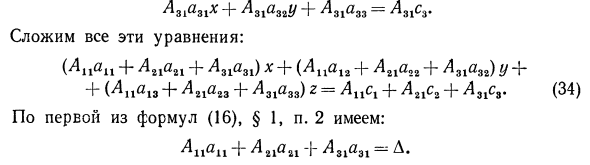


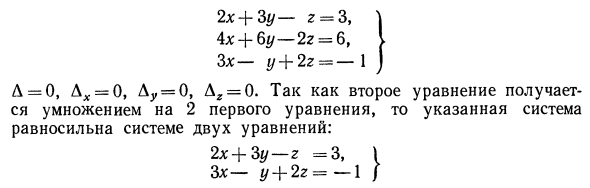

Системы уравнений первой степени
- Система линейных уравнений Примените приведенную выше теорию определителей к решению системы линейных уравнений. (19) /. Система двух уравнений с двумя неизвестными Рассмотрим систему из двух уравнений первого порядка с двумя неизвестными хнами. a21x + a.guy = c2. / В обозначениях коэффициента aik первый индекс означает число уравнений, а второй индекс означает неизвестное число. Решите эту систему.
(Auait — ailavi) x = clatt — ctalt. (20) Точно так же, умножив первое уравнение на (-a21) на член и добавив, добавив второе, feAi-MiJ Y = sgap — saghh. (21) Однако на основе уравнения (2) (см. § 1, пункт I) его можно записать в виде: 2112 「P」 12 «21» 22 * s2ai-say1 = c \ arg ^ r «12 Вверх Cx a.s. CI c-z agg 11 22 Короче говоря, эти детерминанты показаны как: A = Вы есть с, а12 В деятельности Ах = (22) а21 а2т кр ^ 21 a.s. D- Определитель D (19), состоящий из неизвестных коэффициентов системы, называется определителем системы.
Для этого умножьте первое уравнение на π22, второе (–avl) на член и добавьте полученное уравнение. Людмила Фирмаль
Квалификатор DL. (Или Д ^) берется из определителя системы Д, если неизвестные x (или y) коэффициенты ai и a.p (или a12 и a.2.d) заменяются свободными членами cx и c2. С другой стороны, (22)у а? Согласно формуле коэффициента (18) § 1, пункт 2 равен нулю. Таким образом, уравнение (34) принимает вид: A • x = Aps1 + Aisg -f A3lcs. (31 ‘) Рассмотрим детерминанты s, «gg» 13 сг аг, г «23» C * «z *» 33 Если коэффициенты x (т. Е. An, a21, a31) заменить свободными членами clt cs, c3, они взяты из определителя системы D. Разлагает этот определитель на элементы первого столбца.
Обратите внимание, что в этом определителе алгебраические дополнения элементов c19, c3 соответствуют соответствующим алгебраическим дополнениям элементов ai, a21, a31 определителя D, A ps, + L21s2 -f Akhs. = Dx, (35) Сравнение (35) и (34 ‘) Dx = Dx. (36) Уравнение также оценивается D-y = Au и D-2 = Dg, (37) где Значение х может быть подтверждено путем прямой проверки. / г, г «А» 13 «11» 12 С, = «21» 23. A 、 — 「21」 22 3 '', 33 31 » 32 Определители Au и Dt взяты из определителя системы A, где коэффициенты y и r заменены свободными членами. Предполагая, что определитель системы A = ^ 0, из уравнений (36) и (37),
| Преобразование координат | Матрицы и действия над ними |
| Элементы теории определителей | Линейные отображения |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Найти решение системы (33) в уравнении (38). Уравнение (38) называется уравнением Крамера, как и уравнение (25). Подобные уравнения применяются к линейным уравнениям со многими неизвестными. Пример 1. Решение системы Решение здесь 1 2-1 D = 2 -3 2 = -8, Dx = 3 1 1 12-1 2 2-1 2-3 2 = -8, 8 1 1 1 2 2 D = 2 2 2 = -16, Dg = 2 3 8 1 По формуле (38), -8 Если определитель системы Д = 0 и хотя бы один из определителей Дх, Ду, Дг не равен нулю, то система (33) не имеет решения (не совместимо). Конечно, предположим, что ясно, что хχ> 0. В этом случае уравнение (36) невозможно. Это потому, что Dx = 0 слева и Dx = ^ 0 справа для всех x.
Наконец, отметим, что если D = 0 и DX = D ^ = Dr = 0, система (33) не имеет решения или доказательства того, что существует бесконечно много решений. Это иллюстрируется примером. Пример 3. Рассмотрение системы x — (/ 4-2g = 2, 2x-2 # 4-4g = 4, 3x-3 * / + 6g = 3. Где Д = 0, Ax = 0, Ду = 0, Дг = 0. Например, система не имеет решения, потому что первое и третье уравнения этой системы противоречивы. Фактически, умножение первого уравнения на 3 и вычитание третьего уравнения приводит к невозможному уравнению 0 = 3. Пример 4: Система 2 —3 2 = —24. 3 1 8
Пример 2: уравнения одновременности 2x + 3y + 2 = 2, * * —5 # — {- 2r = 3. 4x + 6 * / + 2z = 0 Нет решения, потому что D = 0 и Dx = —44 = ^ 0. Людмила Фирмаль
2x + 3 * / -r = 3, \ 4x — \ — 6y — 2z = 6, I 3x-g / + 22 = -1 j Л = О, Лх = 0, Ду = 0, Ar = 0. Эта система эквивалентна системе двух уравнений, поскольку второе уравнение получается умножением 2 первого уравнения. 2x + 3y-r = 3, \ 3x-y + 2r = -1 j
Есть бесчисленное множество решений. Установите любое значение x, чтобы получить соответствующее значение y и r. Например, если x = \, получить систему 3 года -2 = 1, 1- £ / 4-22 = -4, / 2 11 Решение этой проблемы дает y = —j, r = —y. Когда x = 0, r / = 1 »r = 0 и т. Д. 4. Однородная система первых трех уравнений 3 неизвестных Однородная система, состоящая из трех уравнений первого порядка с тремя неизвестными тревога + al2y + al3z = 0, \ a2lx + a22y + a23z = 0, I (39) a31x + azgu + a33g = 0 Дж В этом случае каждый определитель имеет столбец, и все его члены равны нулю, поэтому Ax = Ay = Az = 0. Уравнения (36) и (37) с. 3
принимает следующую форму: A-x = 0, D.0 = 0, D-g = 0. (40) Для системы (39) и определителя Φ0 система (39) имеет единственное решение x-y-r = 0. Чтобы система (39) имела ненулевое решение, требуется A = 0. Фактически, если x = £ 0, например, A = 0 из первого уравнения в (40). Следовательно, если решение однородной системы (39) не равно нулю, ее определитель равен A = 0. Наоборот, если ∆ = 0, система (39) всегда имеет ненулевое решение. Мы не предоставляем доказательств этого утверждения.
Уравнения (20) и (21) можно записать в следующем виде: Ax = Ax, A * Y = Au. Здесь есть два случая. I. Детерминанты системы = = = = 0. Затем разделите обе части каждого уравнения (23) на D, чтобы получить (24) В L * Или в развернутом виде «12 C * 2 fl «22 «11» 12 я «21» 22 1 Y = «P C1 а21 с2 (25) «II» 12 Уравнение (24) (или 25), называемое уравнением Крамера *, дает решение системы (19). (Рекомендуется проверить это.) Таким образом, если определитель D системы (19) не равен нулю, система имеет единственное решение, определяемое уравнением (24) или (25). II. Определителем системы является A = axla22 — a2lal2-0t, т.е. ahha.r2 = = 212112. В этом случае неизвестный коэффициент одного уравнения пропорционален неизвестному коэффициенту другого уравнения. На самом деле, предположим, что один из них, например ax x 0, обозначен как — = откуда atl = A, au. следующий «И Если ahx22 = a2Xa12, вы можете видеть, что a22 = HaX2.
Учитывая это, система (19) может быть описана как: (26) aixx + ax2y = cx, b (a1Xx + aX2y) = c2. Я Есть два случая. 1) Определители как Ax, так и D, равные нулю: Ax = cx22 — cxaX2 = 0, Au = cmxx — cxai = 0. В этом случае числа a21, a22 и c2 пропорциональны числам, и aX2, c19 и system (19) могут быть записаны в следующем формате: 1 (27) Следовательно, второе уравнение системы берется из первого уравнения путем умножения обеих частей на X. То есть результат первого уравнения. В этом случае очевидно, что в системе (19) существует бесчисленное множество решений. Например, установив произвольное значение //, получается соответствующее значение x = Cl ~~ ai *, J. ах
2) хотя бы один из определителей Ax или Au не равен нулю. Например, предположим, что Au = ais2-a21cxΦ0. a11c2Fa21c1 и, следовательно, c2F \ cx. В этом случае, как видно из (26), второе уравнение ((ццХ + alty) = c2 не согласуется с первым уравнением, поэтому в системе (19) нет решения (или они говорят Не совместимо). Давайте посмотрим на некоторые примеры. Пример 1. Решение системы 2 * + 3 «/ = 7D 4x — 5 * / = 2. / Решения. здесь 2 3 4 —5 3 5 2 7 4 2 D = —22, = -41, D «= = –24.
Поскольку это определитель системы, он уникален для системы Решение определяется по уравнению (24): Ах 41 А. х = — _ U-12 U ~ L 22 11 22 Геометрически это линия, определяемая уравнением (41 12 \ 22 * IT J (CM * GL * § 1, раздел 5). Пример 2. Решение системы Решения. Здесь 2 5 = 0, D = 4 10 2x — \ — 5y = 3, я 4x + \ 0y-6./ 3 5 _ | 2 3 4 6 = 0, = 0 6 10 Второе выражение получается с начала путем умножения обеих сторон первого выражения на K = 2. Следовательно, система эквивалентна одной формуле 2x + 5r / = 3 и имеет бесконечное число решений. Если вы дадите произвольное значение неизвестному y, вы найдете x = 3-5f /. s Например, если * / = 0, * = -2, если = 1, d =, если x-1. Геометрически это означает, что уравнения соответствуют одной и той же прямой. И 4х + 10 </ = 6 Легкий выстрел г. Горячий 5 г
Пример 3. Решение системы 5л 5lg + 3 </ = 7, | 10x-F-6U Решения. здесь 5 7 10 2 5 3 10 6 7 3 2 6 = 0, D = = 36 ^ = 0, D = = –60 ^ 0. D = Поэтому эта система не совместима. То есть решения нет. Мы прямо в этом убеждены. Умножьте и термин, и термин части Добавление первого и второго выражений (–2) приводит к противоречивому уравнению 0 = –12. Геометрически это означает, что прямые 5x-j-3y-7 и 10x + bg / = 2 параллельны и поэтому не имеют общей точки. 2. Однородная система двух уравнений первого порядка 3 неизвестных Однородная система двух уравнений с тремя неизвестными как atlx + at2y + atiz = 0. J Решите эту систему.
Предположим, у вас есть определитель и система записи (28) вида тревога + alttf = -alsz, \ agxx + ag2y = -arzz. J Во-вторых, для любого значения z система (29) имеет единственное решение, определяемое уравнением (25) из 1. | «11-» 13 ^ I —Ahzg ahg 1 —dzz ^ «> 2 «12» 13 я «22» 23 1 «А» 12 я «21» 22 1 G, у = «А» 12 «21» 22 Ах ах «21» 22 „_ 1″ 21-av £ | «11» 121 1 «21» 22 I Используя свойство определителя (см. § 1, подраздел 1), — «132» 12 = _z «13» 12 = Z «12» 13 f «11-» 13 * = -r ~ «23 *» 22 «23» 22 «22» 23 «21-» 23 * «21» 23 так А 13 13 21 23 «11» 12 «21» 22 = / e, то z = k шоу «11» 12 «21» 22 (28) φ0, (29) Ах ах
Подстановка уравнения r в уравнение (30) дает: «12 а1Я а2т а23 「11」 13 «21» 23 «11» 12 «21» 22 х = к- г-к- (31) , * / = -K- Следовательно, все решения системы (28) определяются уравнением (31). Определитель уравнения (31) получается из таблицы (матрицы). «11» 12 «13 v» 21 «22» 23 /Получите различные тройки x, y, r, которые являются решением системы, удалив соответствующие столбцы один за другим и присвоив коэффициенту k разные числа (28). Пример. Решить систему 2x + 3 </ + 5r = 0, \ 6z = 0. / 4а: + 2 года Решения.
Используйте уравнение (31) для получения: 3 5 2 —6 2 5 4 —6 2 3 4 2 = –28k, y = –k х = к- 32 / г, z = k Таким образом, все решения системы задаются уравнениями x-28 &, y — 32 / г, 2 = -8 / г. Прикрепите к конкретным номерам, чтобы получить различные решения для вашей системы. Так, например, если η = 1, x = -28, y = 32, z = -8; h = -: x = 7, * / = -8, 2 = 2 и т. д. 3. Система трех уравнений первого порядка с тремя неизвестными Рассмотрим систему из трех уравнений первого порядка с тремя неизвестными axxx + ax2y + ax3z = cx, \ aa1l: + + a23g = c2, Y (33) ajiX — \ — a3.zy + ar, z = c3. ) Кубический определитель, состоящий из неизвестных коэффициентов р р р ’13 Ах «12 а d = a2X «22 a «31» 32 a Это называется системным определителем. Разрешите систему (33).
Для этого умножьте первое уравнение системы на алгебраическое дополнение Axx элемента axxt, второе уравнение на алгебраическое дополнение An элемента ax, а третье уравнение на алгебраическое дополнение A31 элемента a31. Аххахх Аххах2у А1хахз = Аххшу A2Xa2Xx -J- A2Xa22u -) — A2Xa23 = L21s2 31 «32 ^ / + ^ 31» 33-AllC3 * Добавьте все эти уравнения. (Apai + A2la2l + A3la3l) x + (Aaii + A21a22 + L31aY2) + A 212 + A 31C3 * В первой формуле (16), § 1, пункт 2 это выглядит так: An <* n + Aia% 1 + A3la3l = A
