Оглавление:









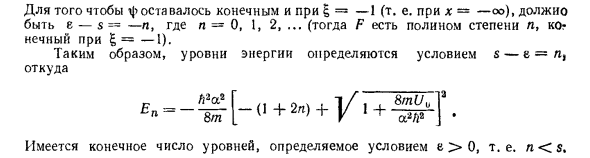

Линейный осциллятор в физике
- Линейный осциллятор. Подумайте о частицах, которые образуют одномерное маленькое кольцо баны (так называемый линейный генератор). потенциал Энергия таких частиц равна shio2x2 / 2, где io является классическим Собственная частота вибрации механика.
Таким образом, Осциллятор Гамильтониан S =? _ + RnuW ‘(23 л) 2t 2 v) Когда потенциальная энергия становится бесконечной Если x = bos, частица может выполнять только компактное движение. Дженни. Согласно этому весь энергетический спектр вибрации Контроллер индивидуален. Используйте матрицу для определения уровня энергии генератора method1).
В матричной форме форма этого уравнения Людмила Фирмаль
Действуйте в следующем виде из уравнения движения Я (19,3), в этом случае они дают x + io2x = 0. (23,2) (^) Mn H «^% mn = 0. Для матричных элементов ускорения согласно (11.8) (X) mn = nn (x) mn = ~ ^ nXmn. Таким образом, (Шт ~ ш) xtp = 0.
Следовательно, все матричные элементы xm n равны нулю, Если не сот = номер все Поскольку он находится в устойчивом состоянии, частота Соответствует переходу nn — 1, т.е. nn, n≥1 = Тогда Являются ли ненулевые матричные элементы xn? Только n = p1. Предположим, что волновая функция φ выбрана Материал.
- Поскольку х является действительным числом, Все матричные элементы xtp одинаковы. кондиционер Митовит (11.10) является матрицей Симметрия: % TP-% PT- Для вычисления ненулевых матричных элементов Ордината использует правило коммутации ^. ^ час хх = хх = —r-, T
Написать в матричной форме (Хх) mp (xx) mp Используя правило умножения матриц (11.12): трет-р ^ Y ‘(^ nlXnlXin3CnNo.ln% ln) -2yV.n1Xn1-%. z z ‘t Я В этой сумме только член I = n = b 1 не равен нулю, Мы получаем (Zn + 1, n) 2- (zn, n_1) 2 = (23,3) Zumunoji Из этого уравнения, количество на изображении (xn + 1, n) 2
так как может содержать Только положительные участники Людмила Фирмаль
Арифметическая прогрессия без вышеуказанных ограничений Будет ограничено снизу, . Потому что мы все еще рты Только относительная позиция государственного номера была обновлена n, но необязательно, если не абсолютный
Сначала возьмите соответствующее значение n-нормальное- Состояние осциллятора. Установить на ноль. матч На самом деле, это jo, -1 нужно считать равным нулю, — ^ ^ ntp • T И последовательное применение уравнения (23.3) при n = 0,1, … Приводит к результатам: о (% N, n-1) — 2 мю
Итак, в конце концов вы получите следующее выражение Для ненулевого матричного элемента с координатами 1: xn, n-1 = xn-1> n = J ^ -. (23,4) 2 р л и Матрица оператора H диагональна, а матричные элементы у вас АЭС желаемое собственное значение Энергия осциллятора. Чтобы рассчитать их, HnP = En = y [(x2) n + u2 (x2) nn т •• 2 21 т / г = ~ | / ^ ^ N1xn1sh1nx1n “b W ^ xnlxln = ~ / Д1 Я -> (<^ 2 + Unl) Xln-
В сумме I только член I = n = b 1 не равен нулю. преобразование Добавление (23.4) En = (n + 1/2) Pn, n = 0,1, 2, … (23,5) Следовательно, уровень энергии генератора Ноо на регулярной основе. Энергия нормального состояния (N = 0) равно Itluj / 2, подчеркивает, что она лучше С нуля. Результат (23.5) также может быть получен путем решения уравнения. Шредингер.
Это уравнение для осциллятора имеет вид Здесь удобно ввести безразмерный переход вместо координаты x. Переменная Ј в зависимости от отношения а = (23,7) Тогда получи уравнение Γ + -e) φ = 0 (23,8) (Здесь простое означает дифференцирование по Ј.) Когда большое большое, 2E / Noo может быть опущено по сравнению с Ј2.
Уравнение φη = ^ 2φ является асимптотическим интегралом φ = = е ^ / 2. (Действительно можно отличить эту функцию их игнорировать φ «= Ј2? /;.) Поскольку волновая функция φ должна оставаться Если t = bc конечно, нужно выбрать знак по показателю степени Минус. В связи с этим естественно создать его по формуле (23.8) Замена. Φ = e / 2X {0 • (23-9)
Функция x (если 0, получить уравнение (вводная запись Поскольку мы заранее знаем, что 2E / Noi-1 = 2ЩE> 0, Тогда n> -1/2) X ~ 2 ^ X + 2n% = 0, (23.10) Где функция% должна быть конечной для всех конечных И Ј = Бос может идти бесконечно Конечный порядок так (чтобы функция φ исчезала).
Решение такого уравнения (23.10) существует только в том случае, если: Положительное число (включая ноль) ла р (см. дополнительное математическое § а), он дает энергию Известное собственное значение (23,5).
матч Решения различных целочисленных значений и уравнения (23.10) Иметь форму X = const • # „(Ј), Где Hn (Ј) является так называемым эрмитовым полиномом, который представляет В полиноме n-го порядка определяется Hn (0 = (-1) ne * 2 ^ — (23,11) Определите const так, чтобы функция φ удовлетворяла условию нормализация + оо J fn (x) dx = 1 -оо Приобретение (см. (А.7)) φ «(x) = (f f) 1 / 4- ^ 5 exp (-Ґ» 1 And n {x \ [^) ‘(23Λ2>
Следовательно, волновая функция в нормальном состоянии Ux) = (r) 1 / «exp (» i: i2) ‘(23’13) Как и ожидалось, для конечного x нет нуля. + оо Вычисляя интеграл f — О Координатный элемент, такой расчет приводит Конечно, к тому же значению (23,4).
В заключение покажите метод расчета Волновая функция fp матричного метода. уведомление Матрица операторов x = b ioox имеет только ненулевые элементы (X-wx) n-1n = — (x + wx) n nr = -r * (23,14) в Исходя из общей формулы (11.11), учитывая, что φ- = 0, Мы получаем (X-gsih) φ0 = 0 Мистер ^ н д
Если вы подставите выражение x = —r ——, вы можете получить его отсюда т дх уравнение дибо тио, -G- = —— г ^ о, Ой р Нормализованное решение (23.13). Кроме того, (X + wx) φn-1 = (x + wx) n) n-1φn = Получить итерационное выражение * ■ = + () ф’- ‘= = — ^ S expf S i M-? ) * -1) ’ N раз приложение к функции (23.13) Выражение для нормализованной функции φ (23.12). Задача 1.
Определить распределение вероятностей различных значений Частота сердечных сокращений. Решения. Вместо разложения волновой функции станции Собственная функция импульса в случае вибрации Радиатору легче исходить непосредственно из уравнения Шредингера в нем. Импульсная презентация.
Назначить оператор координат (15.12) на (23.1) x = ihd / dp, получить гамильтониан в представлении импульса П2 муо2х2 д2 H = 2t 2 dp2 Соответствующее уравнение Шредингера Na (p) = Ea (p) wave Функция выражения импульса a (p) имеет вид дп муй н \ 2т / Эта формула точно такая же, как (23.6).
Поэтому его ре Решение можно описать непосредственно по аналогии с (23.12). так Поэтому найдите желаемое распределение вероятностей в виде: an (p) | 2- = ——— j exp (—— ^ Hn (P ^ dp. 2irh 2pp \ l / tgtioN \ mujh) \\ fmuoh) 2. Определите нижний предел возможных значений энергии вибрации.
Используйте соотношение неопределенности (16.7). Решения. x2 = x2 + (Sx) 2, p2 = p2 + (Sp) 2, (16.7) известно, поэтому среднее значение энергии вибратора — = Ti2 ^ p2 Ti2 (x p2. 1 / с E = —— x2 H ——- ^ ——— (дх) H ——— (Sp) ^ / s, h9 + -. 2 2t 2 2t 8 (Sp) 2 2t Найти минимум этого выражения (как функцию Sp), Каков средний нижний предел? Таким образом, как правило, все возможные нижние оценки Энергетическая ценность: E ^ fax) / 2. 3.
Найти волновую функцию состояния линейного осциллятора, мини Отношения неопределенности, т.е. Среднеквадратичное изменение волновых координат и импульса Кете связан уравнением SpSx = h / 2 (Э. Шрддингер, 1926) х). Решения. Форма искомой волновой функции Φ (x, Ј) = —— ^ ———- ^ e x p | r — ^ —— i (p (t) X. (1) V ‘(27 г) / (<5 г) / I P 4 (Sx) 2’ Координатная зависимость в любое время Следуйте уравнению (16.8). x = x (t) и p = p (t) = mx (t) являются средними значениями Координаты и значения импульса. (19.3)
По линейному осциллятору pa (U = ty2x2 / 2) p = —ty2x, поэтому среднее значение p = —too2x или —o x + io x = 0, (2) То есть функция x (t) удовлетворяет классическому уравнению движения. Постоянный коэффициент (1) определяется условиями нормализации о f | f | 2s? w = 1; в дополнение к этому элементу Ф также может содержать фазы — О
Зависящий от времени фазовый множитель (p (t), неизвестная постоянная Sx И функция <p (t) определяется путем подстановки (1) в волновое уравнение. P2 d2CH! Ti2x2 H ————- Ф = гП- 2 т дх 2 дт Учитывая (2), замена 1 -X X 2) V Tg 4 (5x) 4 5 <(4 4) x 5 (8 2h2 _1 — tr r-Fl) false) 2 H = 0 Отсюда вы можете увидеть (<5g) 2 = h / (2mu). W, j_2 2 ~ 2 часа ^ 1- | и ω = — (x-u x H —-, Ф — рхН —— с. 2p 2 2h 2
Итак, наконец m / mcj \ 1 // 4 dG (x-x) 2 1 r zcjt dg! expi i ‘-at) «rg t» m g (3) Если x = 0, p = 0, эта функция преобразуется в φο (χ) e ~ rb ^ 2-волновая функция Основное состояние генератора. Когерентная средняя энергия осциллятора P2, Ti2x2 P2, Ti2x2 hu / _ l \ … Ј = — + ———- = + ————- h- = hu ha + -; (4) 2 га 2 2 га 2 2 В 2 / Количество, введенное здесь, является средним «квантовым числом» ху конкретной компании.
Он стоит. Последовательное состояние Дайте ту или иную зависимость x (t), удовлетворяющую классическому условию Формула (2). Общая форма такой зависимости может быть записана как: тихий + ip _iut. | 2 _ PG-> T- = ae-I = n. (5) \ J2mnu Функция (3) может быть расширена с помощью волновых функций Состояние осциллятора Φ = ^ apPn, ^ n (x, t) = φn (x) exp | -r ^ ha + ^ ut ^ j.
Фактор этого расширения 1) о an = J (6) — О Таким образом, вероятность того, что осциллятор будет в состоянии ит Я 12 2-н ‘Гб / я-7 \ wn = \ ap \ = e = e-, (7) Ха! То есть дано знаменитым пуассоновским распределением. 4. Определить уровень энергии частиц, движущихся в поле Потенциальная энергия (рис. 3; Ph. Морс, 1929).
Решения. Спектр положительных собственных значений энергии Непрерывный (и уровень не вырожденный) и отрицательный спектр Чтение дискретно. Уравнение Шредингера гласит: U + -Ae ~ 2ax + 2Ae ~ ax) φ = 0 Введите новую переменную 2л / 2тА с = ———— е о (Запускает значения от 0 до + oo) и обозначения (рассмотрим Удельный спектр, таким образом, E <0) _ l / —2tE л / 2т A (1 -s + — Хаха а2
Уравнение Шредингера принимает вид / f ‘I + 1_ / f’ I + ({—1 I + n —- \ — s — \ — l — / — 2 — ^) Ф / = op. Функция oo ведет себя асимптотически как e ± Ј / 2 (1) Па ир Па в Ј-> 0, функция φ пропорциональна Ј ± s. По причинам конечностей Но решение о действии выбрано ^ 4 ° ° для e- ^ 2, и- »0 для Јs. Выполнить замену F = И получить уравнение для ш + (2 s + 1-Ј) w ‘+ nw = 0, (2) Нужно поселиться в условиях yakh: конечно, если w = 0, если w- »oo Это, идти в бесконечность не быстро Менее конечной степени.
Уравнение (2) Вырождающееся уравнение гипергеометрической функции (см. §D по математике) Добавить Cesky) w = F (-n, 2s + 1, 0- Решение, удовлетворяющее необходимым условиям для целого, может быть получено Неотрицательный n (а функция F является полиномом). По словам Определение (1) Следовательно, об энергетических уровнях. о —Ep-A 1- 2 / lP + 2
Где n начинается с 0 и передает положительное целочисленное значение Более важно, л / 2 тА 1 ————> n + — Ах 2 (Таким образом, параметр s является положительным согласно его определению). Там Таким образом, дискретный спектр содержит ограниченное количество уровней. если \ / 2tA 1 Oh 2 ’ В этом случае дискретного спектра нет вообще. 5.
То же самое верно для U = —— ^ — (рисунок 4). о Решение: спектр положительной энергии непрерывен, а спектр отрицательной энергии непрерывен. Реально-дискретный, рассмотрим последнее. Уравнение Шредингера Me? Туо Измените переменную Ј = th ax и введите обозначение л / —2 TE 2mUo = Ј> [Ј> — | «1 |, S = 2 Мы получаем _d „2 ди (1-10 dЈ. s (s + 1) -φ = 0 U {x) 1-е.
Это уравнение для обобщенной функции Le Jendora. Довести до гипергеометрии Замена муминд φ = (1-z2y / 2w (o И временные изменения переменных ^ (1-Ј) = и: И (1-u) w «+ (e + 1) (1-2u) w ‘- (e-s) (s + s + 1) w = 0. Для Ј = 1 (то есть x = oo) конечное решение Φ = (1- ^ 2) Ј ^ 2F [s-s, Ј + s + 1, Ј + 1, (1-Ј) / 2].
Чтобы φ оставалось конечным даже при Ј = -1 (т. Е. X = −∞), e-s = -n, n = 0, 1, 2, … (F — многочлен степени n, Если конечно = -1, это конечно. Поэтому уровень энергии определяется условием s-s = n. 2 Эп = — ак 2 с, 2 а 8 тонн — (1 + 2 р) + д / 1 + Существует конечное число уровней, определяемых условием Ј> 0, т.е. n <s.
Смотрите также:
| Общие свойства одномерного движения | Движение в однородном поле |
| Потенциальная яма в физике | Коэффициент прохождения в физике |
