Оглавление:















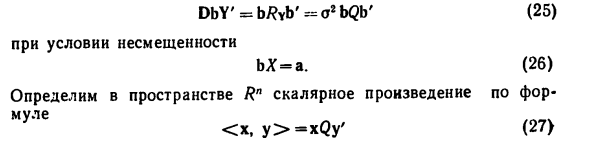


Матрицы из случайных элементов
- Пусть Z = [Za, i ‘= l, …, tn, /=1,…,л] В. З ,, (при т = \ получить вектор-изменение, при л = 1-вектор-столбец; ее элемент). MZ = [MZ, 7, i = \ m, / = 1, …, л], составной из математических ожиданий ее компонента (в предположении, что они существуют). ожидания, очевидно, перестановочен с ооперацией транспонирова- транспонирования: (MZ) ‘= MZ’, математическое ожидание суммы матриц равно сумме математи- математических ожиданий: = MZ <1> + MZ <2>, носятс (МЗ) Б. постоянные матричные множители математического ожидания: Проверим последнее свойство: М (AZ) = [М? AtkZkl] = [? ВйМг *,] = А [Шк1] = 4MZ. 2. Матрица ковариаций.
Пусть U- (? / ,,? / ,, …,? / „) -Случайный вектор. -МС /,), /, / = 1 n] = (U-MU) ‘(U-MU) и приведенные выше правила вычисления математического ожидания- ожидания, получить для матрицы ковариаций векторные U формулу Rv = М ((U-MU) ‘(U-MU)) = MU4J-MITMU. Отметить некоторые свойства матрицы ковариаций. если а-постоянный вектор, то Матрица мат- матрица ковариаций преобразуется по формуле = A’RVA. A)
Действительно, RVA = М (AWA) -M (A’W) M (VA) = A ‘(MU’U) A- -А ‘(MU’) (№) A = A ‘(MU’V- Взрыв в A), запишем для дис- дисперсии ел. в. DUa ‘= #ua’ = a # ua ‘. B) Людмила Фирмаль
Вытекает, что /? И- неотрицательно определенная матрица. Как известно из линейной алгебры, симметричную неотрица- неотрицательно определенную матрицу можно привести к диагональной форма: C’RVC = A C) при помощи подходящей ортогональной пХп-матрицы С: СС ‘= С’С = 1. У меня есть главный диагонали неотрицатель- неотрицательные числа X /, 1 = 1, …, п, а если матрица Rv положительно опре- 81 делена, то все Л,> 0. Домножнм С) слева н справа на матрицу С н С соответственно: Ru = САС = (СЛ ^ КСЛ ‘/ 2)’, где Л1 / 2-диагональная матрица с элементами я) / 2 на главной диагонали.
Полагая СЛ1 / 2 = В ‘, имеем Rv = B’B, D) представлением- Представление D) будет неоднократно использовано в последующем. 3. Ковариации иа лучшеших оцеиок. Воспользуемся формулой A), чтобы найтн матрицу коварна- 6 лучших моделей несмещенных оценок матрицей X полного ранга. Учитывая, что Ry = Rm = o4, получим e = YX (X’X) ~ 1, /? g- = (X’X) -lX ‘/? Y ^ (X’X) -1 = 0 «(X’X) -1. E) Отметим, что если матрица * = [х, ‘х /] состоит из ортогональных векторов х = i = l, …, r, то матрицы Х’Х н (Х’Х) ~ 1 днагональны н оценки в ,, i = \, …, r, некоррелнрованы. Случаи ортогональной матрицы X оказывается интересным и в некоторые другие отношения. требует обращения в матрицу.
- в результате проектирования X, то в случае, когда в процессе анализа отбросить некоторые х:, полагая, что истинные значения коэффициентов коэффициенты при них равны нулю, нет необходимости заново проводить вычисления оцеиок оставшихся коэффициентов процедуре они не изменяются. 4. Пример оптимального выбора моделей моделей. Рассмотрим пример, когда экспериментатор не привязан же- жесткой к данной линейной модели проведение эксперимента и, следовательно, в выборе матрицы X. Допустим, что требуется найтн веса 0, -, i =], …, г, предметы [7]. наилучшей несмещенной оценкой слу: киг выборочное среднее.
Кажется, что а2-дисперсия отдельного нзвешчвання; мету при каждом взвешивании выбирает две группы пред- весов, а затем уравновешивают.Эксперимент может быть описан линейной мо- модель: YQ B i = l, … f n, где хц = —1, +1 или 0 в зависимости от того, положен ли / -Й Веселая или правая чаша весов взвешивание; у, -величина уравновешивающих гирь со знаком, указывающим, на какую из двух чашек добавлен разновес.
Предположим, что X имеет полный ранг, и найдем дисперсию оценки Матрица Х’Х на блоки, выделив угловой элемент: М Ч где b = (xrx2 ‘Хрх /), F-квадратная (п— 1) X (п— 1) -матрица- ца, так что ввиду E) D9, = a2det / 7det; r; r.F) Людмила Фирмаль
Выразим определитель матрицы Х’Х через компоненты разбиеиия. Составим линейную комбинацию последних г — 1 столбцов гХг- матрица Х’Х с коэффициентентом-компонентами-F ~ lb ‘. В результате получите матрицу-столбец: L ь- J Вычитаем ее из первого столбца Х’Х. при таких преобразованиях не меняется, то, разлагая преобра- преобразователь detX’X = det [Hxill2-b /: «lb ‘b Подставляя полученное выражение в F), находим D6, = -о * (|| xi || «—bF-» b ‘) — ». Минимальное значение D6i приобретает, когда вектор Xi имеет самая большая возможная длина, вектор Ь = 0, так как квадратич- квадратичная форма b ^ ‘b’ положительна, если только Ь # 0.
[Проверим, что матрица / • «» ‘положительно определена. Квад- Квадратичная форма положительна, если только а = ^ 0, так как X имеет полный ранг. Для любого вида а = @, а2 ат) откуда следует, что матрица F-положительно определена. 83 Пусть С-ортогональная (я-1) Х (л-1) -матрица (СС ‘= С’СФ = /), такая, что C’FC = A, где Л-диагональная (п — 1) х (я — 1) -матрица с положительны- положительные элементы на главной диагонали. получатель Очевидно, откуда получить bf-‘b ‘= ЬСЛ-‘С’Ь’-ЬСЛ- ^ Л- ^ СЬ’- || ЬСЛ1 / 2 || 2, что и требовалось.] Те же рассуждения применимы и к дисперсии любой другой оценки 6 „i = 2 г.
Итак, чтобы дисперсия оценок коэффициентов коэффициентов 0, -, /=1,…,г, гла минимальна, надо, если это выполнимо, организовать взвешивание так, чтобы, во-первых, содержали нулевой компонент, т. е. при каждом взвешивании участвовали все предметы, и, во-вторых, матрица Х’Х была диа сональиа, т. е. столбцы X ортогональные друг другу. Минимальное значение дисперсии одинаково для всех оценок и равно о2 / п. Если я = г ?, То дисперсия взвешиваний о2 / п в р раз меньше, чем дисперсия o2 / k при fe-кратном взвешивании отдельных предметов и взвешивание Приведем пример ортогональной матрицы из элементов ± 1: А — 1111 1-1 1-1 1 1-1-1 1-1-1 1 При г = п = 4 эксперимент с Х = А приводит к дисперсии оценок а: / 4; при г — А, п = 8, взяв Х ‘= [А’, А ‘], получим дисперсию о2 / 8, в то время как при взвешивании равны соответственно о2 и о2 / 2. 5.
Каноническая форма линейной модели. Рассмотрим линейную модель следующего частного вида: (Л = ф | + а6, -, 1 = 1, …. с; С /, = об i-s + l, …, n, Мб * -О, У-1 я; /? В = /. Г) где II = (L’i, …, i7n) -вектор наблюдателей, ф = (\ | л, …, t |? s) -век- гор тит-iuuecTiibix коэффициентов. 84 по оценкам для моделей G) сильно упрощается по сравнению Чтобы статистика была параграфа. 1 = 1 1 = 1 i = i несмещенно оценивала, скажем, г | 3 [, очевидно, необходимо и дос- достаточно выполнения условий fe [= l, b2 = … = bs = 0. Чтобы ее дис- п 0,2 персия о2У $ была минимальна, надо положить еще bs + i = … … = bn = 0.
Таким образом, наилучшие несмещенные оценки коэф- коэффициентов г |), равны Такие же рассуждения показывают, что наилучшей оценкой па- параметрической функции a [\ |? i + … + as4 | -s будет a [ipi + … + asi | 3s. второстепенная группа G) сама собой напрашивается оцен- оценка дисперсии ^ 5> (8) которая, очевидно, является несмещенной. Покажем, что линейная модель общего вида: У = 8Х ‘+ ое, Ме, = 0, / = 1 п, # е = /, X = [xj, X2, …, х;], 8 = F1 (62, …. 6Г), (9) ортогональной заменой явлений можно привести к виду G), который называют канонической формой модели (9), и получить заново оценки § исходя из оценок ^>. матрица X.
Выберем ортоиормированный базис в пространстве V размерности, порожденного столбцами матрицы X, и дополним его до ортонормироЕанного базиса всего пространства /? «. Обоз- Обозначим через С ортогональную матрицу перехода к новому координаты: и = уС, и- (и ,, …, и „), у = (« / i. •••. Одставляя> |>; =? /, -, I = l, …, s, вместо -ф; в A1), получим слэ следующие отношения для нахождения 6: eX’C = (Ux? / „0 0) .A2) УмноА2) на С’Х, имеем QXfX = (Ul Us, 0 0) С’Х = A3) = (? /, Us, 0 0) [С’х, ‘Сх’,]. По условию выбора нового ортонормированного базиса новые ко- координаты любого типа, из которых начинаются с s + 1-й нулевой: уС = (и, нас, 0 0).
Следовательно, все ясно х, С, я = l, …, r, имеют последние п — с координат нулевых, и потому A3) не изменится, если век- вектор (U \, …, US, 0, …, 0) заменить на (Ui, …, Un): л у / у {Т1 11 \ {*** В Л ^ А ^ Л ^ ‘В ЛЛ В / 1 Л \ чЗЛ Л ^ ™ I С / 1 • • • • i ^ 71 / ^ ^ * ^^ • * ^ * ^ Л ^ ~ Ж 1 * 1 1 «I 4атричное уравнение A4) встречается с нормальной системой уравнения B4) § 9. 6. Оценивание дисперсии. Пользуясь канонической формой G) модели (9), выразим оценка о2 из соотношения (8) = 1, …, я. Из ортогональности матрицы С вытекает л л а из а2) получить, что У U \ = || вХ’С || 2 = 5Х’СС’Хв ‘= §Х’Хв’. 1 = 1 Таким образом, (У ^) (|||| Ц112). A5) н — с \ Аи1 / п — а
Воспользовавшись уравнми перепишем A5) в следующей форме: || pReVY | p = J || Y-§X ‘|| * ТХ ~ ™ S ТХ ~~ ™ S Отметим, что сценка о2-несмещенная, (см. (8)). 7. Обобщенная линейная модель. Обобщим линейную модель, допуская, что компоненты е коррелированы: Y = eX ‘+ oe, Me = 0, #e = Q = [<7 <,, i, / = 1 я]. A7) но при этом мы предполагаем, что матрица Q известна и поло- положительно определена. X полный ранга. виде (см. D)) Q’B’B, A8) где В-невырожденная / iX / t-матрица. Умножая обе части A7) на В * 1, получите Вектор 6 = еВ «‘имеет единичную ковариационную матрицу (см. А)): # 6 = (В-1) ‘# eB- »- = (В’) — 1 (В’В) В-1 = /.
Полагая U = \ B- \ W = X’B- \ приходим к обычной линейной модели: U = 8lP’-ro6, M6—0, Нъ -I, A9) которую матрица W имеет полный ранг. наилучшие несмещенные оценки в обобщенной модели (! 7), поль- мы уже получили известность м;> лелц A9). Пусть d * U ‘-оценка с минимальной дисперсией, 1есмещенио оценивающая аО ‘. 87 является линейной несмещенной оценкой в модели A7), и мы пока она имеет минимальную дисперсию. biY ‘-такая несмещенная оценка аб’, что (B-l) ‘Y = Dd * }’. B0) Поскольку b, B’U = b1Y ‘ несмещенно оценивает аб ‘, а ввиду B0) Db1B’U = Db1Y ‘ = xQy ‘B7) 88 и перепишем условие B6) в виде bQ (Q ~ lX) = a.B8) Задача минимизации квадратичной формы B5) при линейных ог- ограниченность B8) решается в полной аналогии со случаем обычной линейной модели: <2 = /.
Пусть вектор b удовлетворяет B8), тог- тогда вектор Ь *, получаемый проект б в смысле скалярно скалярного произведения B7) на подпространство, порожденное столбца- столбцами матрицы Q ~ (X, также удовлетворяет B8) и в то же время имеет минимальную квадратную длину: = b * Qb * ‘. Следовательно, вектор Ь, приводящий к наилучшей несмещенной оценка, лежащая в линейном подпространстве, порожденном столб- столбцами Q’lX (ср. A6) §9): b = c (Q-iX) ‘= cX’ (Q-i) f.B9) Подставляя B9) в B8), находим с: таким образом, наилучшая несмещенная оценка имеет вид что встречает с B2).
Смотрите также:
| Наилучшие несмещенные оценки в непрерывной модели | Обобщенная линейная модель для семейства сдвига-масштаба |
| Байесовский подход в статистике | Симметричное распределение |
Если вам потребуется помощь по статистике вы всегда можете написать мне в whatsapp.
