Оглавление:




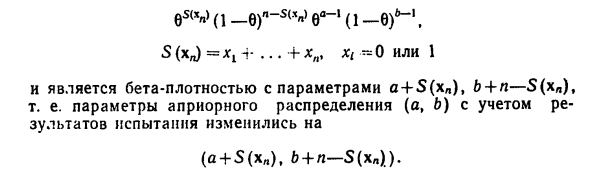




Байесовский подход в статистике
- Неопределенность экспериментальных результатов в объяснении статистики Статистическая модель ($?, L, {Re, in ev}) состоит из двух частей 168 компонентов: стохастическая неопределенность, Из-за случайного характера механизма, который реализует х в соответствии с распределением Неопределенность, связанная с распределением вероятностей Re, n Незнание истинного значения 80 параметра 8 Реализовать х. Байесовский метод в статистике Рассмотрим вторую неопределенность со стохастической точки зрения Вероятность.
Например, рассмотрим задачу выборочного контроля производства Прошлый опыт Обобщается в виде установки распределения вероятностей Q Параметр 0. Укажите соответствующее случайное значение с помощью O Значение. В результате получается пара случайных элементов X и B. / c (x) и f (c) — плотности распределений Po и Q соответственно Соответственно. Затем пара (X, c) имеет плотность / in (x) / in (8).
Производство, когда параметр 8 описывает некоторые свойства партии Продукт и может рассматриваться как случайное изменение С вечеринки на вечеринку. Людмила Фирмаль
Более чем Зависимость ели от случайной выборки X. с. Характеризуется Условная плотность / х »WeWe00: A) Вы можете себе представить, что смысл еды первым понятен. с. 0 по плотности / «(9)» в соответствии с условной плотностью Случайный образец плотности A) X сформирован. Значение 0, принято Принято. с. C, неизвестно, случайная выборка x, значение x можно наблюдать Наблюдалось. По результатам наблюдения x нам необходимо сделать выводы о: Значение 0. Байесовские статистические модели называются структурами Состоит из статистических моделей ($?, Ev, {P „, web}) и измеряется Измеримое пространство @, & ~) и его измерение вероятности Q,
Это называется предварительным распространением. Выбор предшествующего является фундаментальным Байесовский момент. Например: Выше распределение Q является Частота из прошлых наблюдений Феномен очень маленький. В теории различные Разные подходы к этой проблеме. Суть проблемы заключается в Из предварительной информации или заранее Неформальное представление стохастических задач @, & ~) Распространение. Не здесь По этому вопросу, несмотря на различия Наконец, частота и байесовская методология в статистике В конечном итоге приводит к эквивалентному статистическому процессу Процедура. Если априорное распределение Q выбрано каким-либо образом,
- Проблему оценки нуля можно отнести к области чистой теории. Вероятность. Случайные элементы измеримого пространства @, ~~) с распределением Q полностью определяется его распределением Распределение вероятностей. Информация о 0 включена в дело 169 Образец чая Х полностью условной плотности (Учитывая множество {x: fx (x)> 0}): / в | X (b | x) — / xv (x, b) // x (x) = — / e (x) / in (8) // x (x) = / X | in (x19) / in (9) // x (x), B) Где мы предполагаем, что измерения Po и Q задаются плотностью Плотность / x (x) = J … J / e (x) / e (e) дет … d9. «С) Мили и Параметр 9 условной плотности B) называется post-hoc. Формула Б) является непрерывным аналогом, Это называется теорема Байеса.
Примите соглашение, чтобы избежать введения ненужных обозначений. Для дискретного X ниже плотности / in (in). / q (x) и Например, соответствующее распределение может быть понято. Вероятность: Pe (x), Q (9) и т. Д. В этом случае уравнение Б) Если X или in является дискретным, сохраните предыдущую форму в уравнении C) В дискретном случае интеграл заменяется суммой. да Задняя плотность B) служит всем источником Дальнейшие статистические выводы по 9 Как правило, оценка будет принимать среднее значение этой плотности. t = l, …. *, D) где Мы «lx) = 1-1 / eix (8lx) dei •••• de-« de. + «••• d <> *
Простой в понимании метод конвертации Формула B), C), количество X, дискретное или оба Discrete. Людмила Фирмаль
Задняя плотность компонента 6i вектора e = Fi, …, Рассмотрим пример модели Байеса. (I) Пусть (X \, …, Xn) = неизвестно в тесте Xn Бернулли Вероятность 0 <9 <1, ранее бета Бета-распределение плотности B (a, 6) -‘bv- | A-9) * », 0 <9 <1 (см. Раздел) 5§7). Задняя плотность B) пропорциональна eS (x «> (I_e) n-s e» A —bN, S (xn) = xv h- … + xn, X [^ 0 или 1 И бета плотность с параметрами a + S (xn), b + n — S (xn). То есть параметры априорного распределения (o, b) Результаты теста (A + S (xn), b + n-S (xa ).
Априорное среднее для параметра 9 (см. §7) 1 UB (a, b) -16e A-c) * ~ |? W = B (b + 1.B) / B (a, b) ^ a / (ab), о И последний является {a + S (xn)) / (a + b + n). Если число наблюдается Если наблюдаемое значение n велико, байесовская оценка (a + S (xn)) l (a + b + n) S (xn) ln приближается к частоте независимо от a> 0 и b> 0 Положительные результаты теста Бернулли. (II) Пусть X \, .., X — независимая ель. с. экспоненциально Априорное распределение с плотностью С (О, I), параметр 9- G (}., P) и X, p затем задний плот Плотность пропорциональна Q «e-s ^ n) ebP ~ \ e-M) 8> 0,5 (xn) = X \ — <-… + xn,
То есть плотность распределения G (\ + S (xn), p + n). Найти байесовскую оценку функции надежности априорное среднее значение exp (-90 равно J о о Jro «) \ * — + t) Jro») Ой ой Априорное среднее значение exp (–0 ^) ))) — («+ I» E) Если n большое, байесовская оценка E) близка к лучшей Несмещенные оценки (см. Пример (VIII) §17): Однако байесовская оценка дает следующие результаты: t> все t, включая S (xn). да Лемма 1. Сделайте T (x) достаточной статистикой Статистическая модель {&, 28, {Rv, 9ev}). После этого, @, Априорное распределение Q от 3 до Подмножество X с любыми 9 Pn единицами измерения / in | X (in | x) = / in | T (X) (9 | 0, t = T (x), F) Если плотность, включенная в F) дискретного случая, можно понять
Это понимается как распределение вероятностей. 171 Выполните доказательство непрерывной модели. Крит Разложение RPU (см. §16) / e (x) = f {(x) = g (T (x); c) A (x) G) Подмножество X с P ^ -измерительной единицей, 8e6, Задняя плотность пропорциональна (см. B) * (T (x); c) / in (9). (8) Плотность / дюйм | m (x> (®I *) ‘^^ (x) также пропорциональна Он пропорционален правой части (8). Уравнение B4) Согласно §16 /? <x) @ = -? (‘; E) Mt), Оттуда уравнение B) применяется к паре T (X), c, / B1T (X) (11:00) пропорционально (Т6) / (9). (9) Сравнение (8) и (9) дает утверждение леммы. да Лемма 1, от байесовского подхода к понятию Удовлетворение играет ту же роль, что и классическая статистика. Статистика. То есть из уравнения F) достаточно Согласно статистике, заднее распределение B Условие выборки x, это все, что вам нужно знать на байесовском Метод.
Смотрите также:
| Наилучшие несмещенные оценки в дискретной модели | Матрицы из случайных элементов |
| Наилучшие несмещенные оценки в непрерывной модели | Обобщенная линейная модель для семейства сдвига-масштаба |
Если вам потребуется помощь по статистике вы всегда можете написать мне в whatsapp.
