Оглавление:




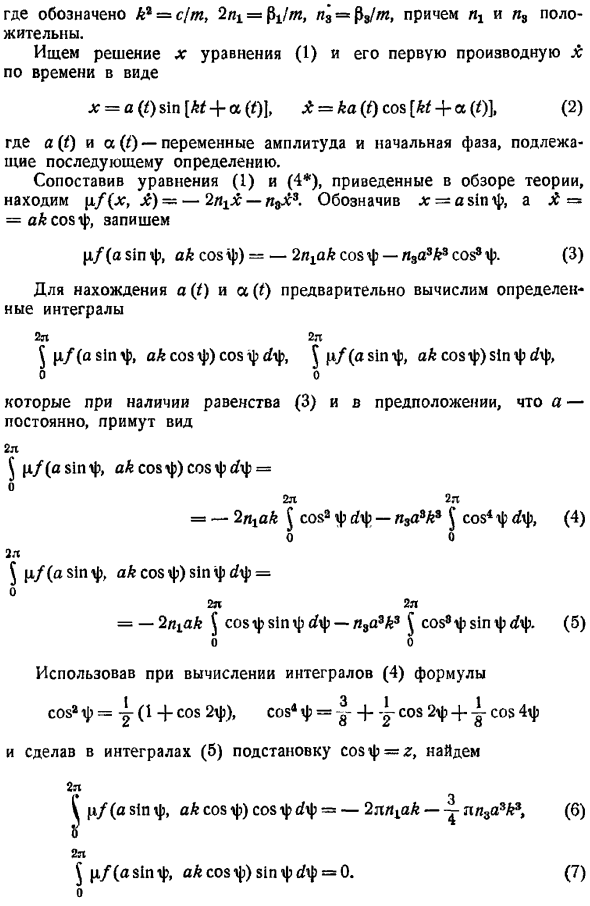



Метод медленно меняющихся амплитуд (метод Ван-дер-Поля)
- Этот метод полезен, когда движение материальной системы описывается дифференциальным уравнением с малой нелинейностью. Х А х я i. 4. Где f x, i -нелинейная функция x и, А p-малый параметр. если f x, f 0, то уравнение 4 будет линейным I A x 0, общее решение которого, как известно х asln Ш А, х aAcos а а. В 1926 году Ван дер Поль предложил, что для малой нелинейности общее решение Формулы 4 и ее первая производная имеют внутренний индекс, соответствующий линейному уравнению 2×0. х грех т а, я Ак COS в т а, 5 Где амплитуда а и начальная фаза а-медленно меняющиеся функции времени а а 0, х х 0. Этот метод позже Л. И. Мандельштама и N. D.
Было продемонстрировано математически в исследовании папалекси. Мы видим, что это нелинейное дифференциальное уравнение 2-го порядка 4 эквивалентно 2 нелинейным дифференциальным уравнениям 1-го порядка. a j — asinij , ak cos , a — asinifi, ak cos , где вводится обозначение. Вместо этих точных уравнений было предложено закрепить приближение-уравнение, полученное из укороченного 6, заменив правую часть соответствующей средней величиной в диапазоне от 0 до 2, то есть правой стороной. 2р Если а 2 ф asinTf, аль cosxj з-рН, 7 2р a — a slnф cosФ sln 4 8 При вычислении правых интегралов этих приближенных нелинейных уравнений амплитуда a должна считаться постоянной.
При вычислении момента инерции однородного трехмерного твердого тела относительно некоторой оси выделяют в твердом теле-такой элементарный объем, момент инерции которого относительно соответствующей оси известен, либо легко может быть определен. Людмила Фирмаль
Интегралы дифференциальных уравнений свободных колебаний с малыми нелинейностями методом ван дер поля рекомендуется выполнять в следующем порядке 1 Создайте дифференциальное уравнение свободной вибрации и запишите его в виде 4. 2 взять x a sin f, x aAcosif и вычислить определенный интеграл 2-й 2-й Дж. Ф. грех доктора, Ак sovf sovf Ф, asinty, Ак cosф sinф ф При рассмотрении константы 3 Добавить результат предыдущего абзаца справа от укороченного уравнения ван дер поля 7 и 8. 4 интегрируйте уравнение 7 и вычислите полное интегрирование Ф, ст 5 присвоить полученные значения a t, Cj укороченному дифференциальному уравнению 8 и интегрировать его, вычисляя общий Интеграл a a f, Cb C9.
Подставляя полученные значения a t, Cj и a t, Cy Ca в уравнение 5, определить начальное условие заданного движения 0, x x0, I интегральная константа C 7 полученные значения Ci и Ca вычисляются в пунктах a A Z, Cj и a a т. е. если вы хотите добавить к нему значение, вам нужно добавить его в Cy Cg. 4 и 5 8 подставляя искомое уравнение движения О грехе А М Значения a t и a , полученные в предыдущем пункте. Задача 20.3.Решите задачу 20.2, используя метод медленного изменения амплитуды. Решение.
Напишите рассматриваемое дифференциальное уравнение 4 20.2 по форме Ф 2е р р 1 2 Найти решение в виде Формулы 1 и ее производных первого порядка Ф ж грех В а т, ф А А Т, потому что Т А я Джей 3 Где переменная амплитуда в 0 и переменная начальная фаза а 0 являются предметом последующего определения. Если сравнить уравнения 1 и 4, приведенные в обзоре теории, то в этом случае x p Ф. ф ф СР a sin , и P aAsozph аз nf, а A cos f a s1a f. 4 0 и 0, предварительное вычисление определенных интегралов 2р 2р м НП, aAco5p Софья 7п и J a81pf, aAco8p 81pf1 Ф 4 в предположении, что существует и величина а постоянна Ф грех Ф Ак со Ф соз ф ф А Й грех Ф со Ф Ыф 2л 2л J A sin , ak cos sin a J sin.
Если использовать подстановку sfnif z с первым интегралом b , а во 2-м Интеграле 5 с выражением sin ij — —soz2p at sob4p Второй Дж. Ф. Син Ф Ак со Ф соз Ф с ф 0 2л Ф А sin , Ак при cos sin — — Ла. 6 Вводя значение интеграла 6 в укороченное уравнение ван дер поля 7 и 8, приведенное в обзоре теории и рассматривая 2 а 0, д 7 Из первого выражения 7 е 0-ср. 8 Если вы присваиваете 8 2 — му выражению 7, то оно имеет вид a — AC .Когда вы интегрируете Подставляя результаты 8 и 9 в Формулу 3, можно найти -C,, 1n 4 1- C С, , 10 4.-4C1eo1 я л-ЛК с,. 11 В 10 0, p a0, 11 вводя t 0, p 0, получаем систему уравнений a0 ClsinC2l 0 ZrCj cos Sc.
- Если вы решите эту систему, у вас будет Ci a0, Ct n 2, если Cj 0, то решение системы будет потеряно вообще. Подставляя полученные значения Cx и Ca в 10, находим искомое уравнение для колебаний маятника. Ф conv convl 1 — 12 Как видно из 12, круговая частота p колебаний маятника, согласно его начальному угловому отклонению a0 — — ..И 13 Если мы решим уравнение 12 и результат задачи 20.2 21 способом, расширяющимся с малыми параметрами, мы увидим, что метод ван дер поля производит первый первичный член уравнения 21 задачи с несколько меньшим вычислительным весом. Оказывается, что размер циркулирующей частоты p, найденный двумя способами, одинаков см.
Уравнение в вопросе 20.2 13 и уравнение 20. Поэтому применение метода ван дер поля для определения первого приближения должно считаться целесообразным и эффективным. Задание 20.4.Материальная точка массы m движется вдоль оси x под действием упругих сил и сопротивления. Его проекция Fx — ex, Rx — Pi — Pz — 3, соответственно. C Pi и Pz положительны constants. At начальная точка, точка находилась в крайнем положении, определяемом координатой x od, и была выпущена без начальной скорости. Найти уравнение движения точки с помощью метода ван дер поля. Решение. Дифференциальное уравнение движения точки mX Fx Rx.
Затем определяется искомый момент инерции однородной плоской фигуры путем суммирования моментов инерции всех элементарных площадей. Людмила Фирмаль
Для конкретных значений Fx и Rx ТХ — СХ-видеорегистратор PTX-Pax3, или Х х — р а-P3X3, 1 Ниже эта задача решается эквивалентным методом линеаризации задача 20.5 с сравнительной оценкой различных решений. Вот, кг с m, 2ni fiilm, n 3, m, 1 И л положительны. Мы ищем решение Формулы 1 x и ее первой производной, A, в виде х а 0 грех а 4- х 0,а аа 0 потому что а 2 Где a и a — переменная амплитуда и начальные фазы, которые подлежат последующим решениям. Если сравнить уравнения 1 и 4, приведенные в обзоре теории, то можно сказать, что p, f x, j — la 3 найдено. asinij , Л AA cosip, пиши с sinф, Ак cosф −2лхаАcosф-Лза А8 cosф.
Предварительно вычислите определенный интеграл, чтобы найти и t 2р 2л J p az1pf, и a cos f cos f b f, c a81pf, ak cosf sin f t f, учитывая уравнение 3, в предположении, что A-постоянная 5 часов вечера b81pf, fl A COS f COS f b f — 2л А. Дж коза ф т ф-Lzd А3 Дж Коза Ф УГ, 4 с a81pf, Ак со Ф грех ф т ф −2 ща Дж cosфsinфсГф-л8а3А3 cos3фsinфф ф.
Формула, используемая при вычислении интеграла 4 потому что ф у Я cos2ф, cos1ф А cos2ф 1 cos4ф И если вы присваиваете SOF x интегралу 5 2р Джей с ф грех, Ак cosф cosф ф −2пп Ак-Джей nn3a3A 6 Путем введения интегралов 7 и 8 в укороченное уравнение ван дер поля 6 и 7, приведенное в обзоре теории Формула 8 Если вы разделите переменные, вы найдете r mt С другой стороны Мы пишем 8 9 У Если мы интегрируем это уравнение Иначе говоря В-в 1 л ы Ки — П Здесь Интеграл константы CI является предметом для последующих решений. решение уравнения 11 на a Интеграл уравнения 9 равен 13 Введем результаты 12 и 13 в уравнение 2. х грех м Джи — Е-Р 1. потому что Т КТ С. В.
Если подставить начальные условия i 0, x-a0 в уравнение 14 и присвоить начальные условия t 0 и jf 0 уравнению 15, то получим уравнение. После решения этой системы C4a 2, Cj V14-X2a a0..Узнайте больше. Используйте эти значения Cx и Cj для описания желаемой подгонки в следующей форме КЛ х 1аи-Ся Ле-2njl Потому что КТ.
Смотрите также:
Предмет теоретическая механика
