Оглавление:













Метод потенциалов
- Метод сдерживания Двойная задача Написание математической модели Стандартные проблемы с доставкой для предыдущего удобства Умножьте первую группу ограничений на -1. необходимо Минимизировать функцию tη ζ {Χ) = ΣΣ ^ ΧίιΟ) £ α = 1 / —Ι В условиях η -Σ * ν = —βι. ί = 1 «… ・ / η; (2) / «Ι м Σ # * / = b / ι / = 1η ‘> (3) * ί /> 0; ί = 1, …, m \ j = 1, …, η. (4) Задача (1) — (4)
- Асимметричный двойственный, Указывает переменную, соответствующую строке (или Таблица ограничений) (2) и столбцы (или ограничения) (3) Транспортные задачи через u (I = 1, …, m) и Vj (j = 1, …, η) соответственно. Нужно максимизировать линейную функцию lτη f (u, ν) = Σbfli-Σ <W / (5) / = Ιί = 1 Под ограничениями Vf-nK cih I = 1, …, м; / = 1, …, I (6) Для первой основной группы транспортных ограничений.
Задача не умножается на -1, и вы можете получить другую задачу Эквивалентная форма двойной задачи для транспорта. Людмила Фирмаль
Это Задача состоит в том, чтобы максимизировать функциональность ηt Γ (u, ν) = Σbm + Σam (7) / -ι <_ι В условиях Vj + Ui <cu, / = 1, …, м; / =! , …, я. (8) 101 Более общая форма двойной задачи Во-первых, задачи (5) — (6). Двойная переменная u и u Часто упоминается как потенциалы строки и столбца, соответственно Таблица транспортных вопросов. Приемлемые базовые критерии оптимальности решения Транспортное задание.
Сделайте это приемлемым Базовое решение X =(i * /), i = 1. ·. , M } = 1, …, ηtransport Задача. Возникает проблема: при каких условиях это будет Это оптимально? Необходимые и достаточные оптимальные условия Впервые доказано Л. В. Канторовичем. Это состояние необходимо. Используйте двойные задачи для транспортировки. в качестве Теперь давайте рассмотрим задачи (5) — (6).
Теорема 6. Допустимое базисное решение X = (x (i), t = 1, …, м; / == 1, …, η, задача транспортировки оптимальна Только если найден такой номер Потенциал s— (= = 1, …, m) и r> f (/-b…n) Строки и столбцы таблицы, удовлетворяющие следующим требованиям: условия: vf-Ut = ец (для основной перевозки) (9) и Oi-ui <Cii (для неосновной xi) t (10) Прежде чем доказывать теорему, эквивалент Формат записи оптимальных условий (9) — (10).
Представляя Это Cij = Vj-вызов этих величин (сс) косвенно Стоимость (стоимость перевозки). Тогда соотношение (9) — (10) Принять форму / -Cs-Cs = 50 (для основного xq) * (11) и Δ; / = cc-cc <0 (для неосновныхcc). (12) Условия (9) — (10) и (11) — (12) обычно называют условиями Потенциальный транспорт X. Во-первых, в устной форме, эти Условия формулируются следующим образом, например:
Разница потенциалов, Все столбцы и строки ячеек в таблице для конкретной задачи Меньше, чем соответствующая стоимость доставки, Заполняющая (базовая) ячейка, должна точно соответствовать На эти расходы. Если план транспортировки соответствует Состояние потенциала, это называется потенциалом.
Теорема 6 может быть сформулирована в терминах принятых условий. В противном случае: для оптимальности основного решения допускается Такая возможность необходима и достаточна. Доказательство. Достаточно. По какой-то причине Решение X = (x (I)> ί = 1, .. m t \ \ = 1, …. n, выполнено Скрытое условие (9) — (10).Докажите, что X оптимально Решения транспортных проблем.
Очевидно, что потенциал Ut (i = 1, …, 102 (9) — (10), удовлетворяющие условиям r) и v> / (/ = 1. Возможное решение двойной проблемы. Любое решение u, vf (i = 1, …, u; / = 1, …, n) Двойная задача Для него vf-u а и Σxz = a *. После этого выражения (15) Принять форму ηtη 5 = Σvfii-ΣΜΑ «и неравенство (14) -Σν $> \ — \ шт \ ί «1 /=-.1 t tη -Σ «l <ΣΣ сухо т =! j = l / 4 = 1 Или f (u \ v ‘) <Z (Xi).
Последние отношения могут иметь любое значение Линейный функционал двойной задачи Значение целевой функции исходной (т.е. транспортной) задачи. Как и основная теорема теории двойственности, Осталось это показать ηt tη Σbfli-Σam = ΣΣscx. (16) / -! ί = 1ί => 1 / = 1 Посмотрите на правую часть формулы (16). Сложить и вычесть ηt Σbpj-ΣSCST- рядом ί— 1 т = л t \ tηtη ΣΣea * u = ΣΣ <* / * 0— (Σ * w —Σb) + ί-1, -i i = l /=.1 \ yeiί-l / в м \ мηΙηm + (Σ * ν «ν — Σam) = ΣΣ» ί / ^ ί / — (Σ «ζΣ% —
Но из латентного условия (9) — (10) это -Vj + Ui) xij = 0f Факторы для основного транспорта dj-Of + u = 0, неосновная -xi = 0. Таким образом, tη ΣΣ (% -ν, + Щ) хц-0, Следовательно, уравнение (16) следует из (17). Необходимость. Пусть X = (xi), i = 1, …, m ] = 1 η является лучшим решением для транспортных проблем. Покажи это Удовлетворить потенциальное условие (9) — (10).
По словам Теорема теории двойственности, оптимальная Решение двойной задачи для ui% V \ (i = 1, …, m \ / = 1, …, η) Что касается транспорта tηηt ΣΣ · / * / = Σvfif-Σ ад. (Ϊ8) Докажите, что все числовые значения ι и ι> не являются Для условия (9) — (10) уравнение (18) невозможно. принимать Отношения (18) tηtηIn m \ ΣΣscc = ΣΣ число * —υι + id xc + (Σfl / fy —Σ “* dD i »l / = 1 i = M, =, 1 \ / = l i *» l / Для оптимального решения wc-vt + u> 0.
Если условие (9) — (10) не выполняется, существует такая индексная пара (/, K) (Clk-Vk + Ul) Xlk> 0 Последнее показывает, что это невозможно, учитывая (19) Равенство (18). Полученное противоречие доказывает теорему. Потенциальный метод алгоритма. Алгоритм потенциального метода Построен по теореме 6 и разделен на запчасти Первый шаг расчета и общая итерация Получите оптимальный шаг решения.
Подготовительный этап. Этот шаг включает в себя следующее: Три этапа себя: 1) Постройте начальное приемлемое базовое решение. 2) Найти потенциальные точки производства и потребления. 3) Проверка плана транспортировки, полученного на первом этапе О возможности (оптимальности). Это решение Если он окажется оптимальным, процесс расчета заканчивается.
В противном случае вам нужно перейти к общему повторению Step. 104 На первом этапе основное решение транспортной проблемы Любой из известных способов, например По северо-западному углу или по методу минимального элемента. Мы будем все Продемонстрировать основной принцип работы алгоритма на примере 2 в этой главе.
Принять в качестве первого базового решения Получил это задание По северо-западному методу νιυ * va ° 4 Второй угол. Решение Хо Матч транспорта Равная стоимость Z0 = 110. На втором этапе Каждый предмет Производство и потребление Потенциал u (i = 1, …, m) и 1 // (/ = 1, …, n). Удобно записывать Каждый справа и На вершине построено Исходное базовое решение Хо.
Потенциальная стоимость строки и Столбец находится по уравнениям одновременности (9) Первая часть самого потенциального условия планирования Транспорт. Эта система линейных уравнений {VJ-Ui ^ Cq для Основной транспорт} включает уравнение m + η-1 и m + η ·. Переменный. Так что есть бесчисленное множество решений. Каждое такое решение подходит для подтверждения плана перевозки.
Хо для оптимизации. Найти решение Потенциальное значение выбирается произвольно. На практике в большинстве случаев рассчитывают вручную Предполагается, что для системы существует нулевой потенциал. Для этого примера построим следующую систему уравнений: Вычтите каждую занятую (базовую) ячейку из потенциала столбца Равно возможности строки Коэффициенты целевой функции:
V \ -и \ = Cs = 1; v \ -u2 = c2 \ = 4; s-from = C3 \ = 0; v2- «s = c32 = 2; from-from = szz = 2; u-out-szl = 4. m + n-1 = 3 + 4-1 = 6 уравнений и m + η = 3 + + 4 = 7 переменных. Установить из = 0, тогда υ \ = 0, υ2 = 2, V3 = — 2, ^ 4 = 4, \ = -1, α2 = -4. На третьем этапе накладные расходы ss = 0 / — -у а разница Δ ^. В этом случае, на наш взгляд, удобнее уменьшить Они каждый в двух таблицах В этом примере строится таблица косвенных значений Таблица различий.
N Я «1- что L0 — I2 «S- \ 1 \ л 1 2 3 1 | 10 4 10 0 • 20 2 2 0 3 0 2 5 5 3 3 0 2 0 2 5 5 1 4 1 2 0 0 о 4 10 10 10 10 20 105 / о 1 -1 * (Q /; = -4 4 0 0 3 6 2 3 ! 6 2 5 8 4 0 Δ // = Ο 0 +1 + ч 0 0 +4 0 + ч +8 0 Найти лучшее базовое решение. с того времени Разница положительная и вообще идет Повторите шаг. Общий повторяющийся шаг. Будет выполнен на этом этапе Переход к новому базовому решению транспортной проблемы.
Для Это так же, как симплекс метод, Стоимость доставки определена в базовом определении. во-вторых Этапы-их номера и транспорт Решение этой проблемы. Первый этап Перевозка включена в базовое решение Это связано с наибольшей положительной разницей Δ ,. е. Таблица ячейка с наибольшим количеством нарушений Оптимальное состояние.
Предположим, max (ss-aj) = Δ / Λ. Тогда вам нужно ввести xn Доступные транспортные планы. В этом примере (ss-%) = 24 = 8, поэтому Решение Хо ввести груз № 24- Второй этап t + η-1 до основных грузовых перевозок вот это да Введено решение (# / *). Найти ее Числовое значение таблицы базисного решения t = xik> 0 Постройте так называемый цикл пересчета.
Ячейка таблицы вызовов Начальный (начальный), соответствующий вводному транспортному xik Клеточный цикл. Перечисляет основные правила построения цикла. 1. Все ячейки в цикле, кроме оригинала, должны быть базовыми. 2. Две соседние ячейки соединены прямыми отрезками. 3. Соединительные сегменты нужно пересекать только под Прямой угол, то есть поворот от одной ячейки в цикле к другой Беги под прямым углом. 4.
- Графически цикл должен быть замкнутой пунктирной линией, ссылка Пересекаются под прямым углом 5. В любой строке или столбце с ячейками в цикле Должно быть ровно две вершины цикла. 6. Исходная ячейка цикла всегда отмечена знаком +. Остальные +, -, и любые два соседа Клетки были отмечены напротив.
Клеточный цикл, Так называемый, отмеченный знаком плюс (минус) Положительная (отрицательная) половина цепи и сам цикл — замкнутый Сеть. Наиболее распространенный термин в последнем случае Это первое. Замечания. Пометить ячейки знаком плюс (минус).
Это становится понятным снизу и означает прибавление (вычитание) к Содержимое этой ячейки Значение /> О решении Транспорт а / л. Людмила Фирмаль
Построение петли Проводится за столом Базовое решение доступно (X0). Некоторые основы Различные форматы цикла Рисунок 12. Следует отметить следующее Вершина этого цикла — отпуск. 12. Это может быть рано. Перепишите план здесь для ясности Транспорт X0 и цикл преобразования с самого начала на его основе Ячейка, соответствующая # 24.
После строительства Содержание цикла Положительный (отрицательный) Увеличение полуцепи (Уменьшение) t> 0. Операция такая Вызывается цикл смены Значение L То же / то есть, Введено в коляску xik9 Основное решение Определяется из Соображения: 1) трафик m + η может участвовать в цикле. 2) Основные решения основных транспортных проблем Существует ровно m + n — один транспорт, их транспорт строго положительный, м + η-1 или более 3) неотрицательное число /
Содержимое каждой ячейки в отрицательной полуцепи после циклирования Сдвиг на t был числом больше нуля. Исходя из этих требований, транспорт xtk = /, Вводится в базовое решение, равное минимальному числу В содержимом отрицательной полуцепи клетки chz, т.е. xik = t = min (xz) — Предоставить этот выбор / новый план Перевозка разрешена по причинам, указанным в смене Поддерживать баланс строк и столбцов таблицы.
Это естественно Тот факт, что каждый цикл имеет сдвиг Две ячейки в этом ряду и в каждом столбце. В любом из этих ми * ми * м τ τ <С-4- Я Я 1 * 4 ^ Я! Я π R ΐϋ ЗЛ-ч ( ΎΎ > Ί ΙΧΙΊ 1 2 3 по 1 10 1 4 10- о + 20 2 2 0 3 ίo 2 5 5 3 31 0 2 ίo 2 5 5 4 2 0 0 0+ 4 10- 10 αΊ 10 я 10 20 107 Добавьте t-клетки и вычтите из другой ячейки. Вот так Баланс между строками и столбцами не теряется.
Написать формулу для расчета компонента Xil в результате плана транспортировки Чи Сдвиг существующим решением Ho t: [хц- Основные поставки, не включенные в цикл. х’ц = Ixti-t — для отрицательных полуцепочечных клеток. l * f / + ‘-Для положительных полуцепочечных клеток. Замечания 1. Предположим, что найденное значение заменяется на ноль Несколько вагонов были разыграны.
Тогда получите новый базовый Решение с (t + η-1) -ым основным переносом требует одного из следующих: Выйти из плана перевозки, а остальное следует считать нулевым Основные. В этом случае вырождается решение. Замечание 2. Находясь в положительной полуцепочечной клетке цикла Нулевая база, положительное значение после смены Номер.
Если такая ячейка входит в отрицательную половину цепи цикла, Тогда при t = 0 заштрихованный ноль перемещается в транспортную ячейку xlk. как Значение целевой функции нового плана транспортировки отображается Осталось прежним. В этом примере x2 * = t = min (10, 10) * = 10. Сдвиг на t = 10. Очевидно, x2 \ = * s4 = 0. Примечания, одна из этих отправок, например * 2 Ноль.
В результате Сдви нас Основное решение Время объявления Симплексный алгоритм Метод расчета Значение линейной формы Повторите набор Формула Zk = Zk-1- -t max (Ζι-сι), где Zk А зк — \ — значение Основная целевая функция Решение актуально Числа k и k — 1. Аналогичная формула Транспортное задание: Zk = Zk + 1 / max (c * / -Cs). (20)
Если план х \ фрахтовые расходы равны Z \ = Zo-imax (ct7-ss) = PO-10 -8 = 30 Из уравнения (20) план транспортировки т * = 0, значение целевой функции не изменяется. В новом базовом решении они делают то же самое А с предыдущими, т.е. они возвращаются на предварительный второй этап Шаг и т. Д. Это Лучшее решение, а именно Таблица разностей не включает положительные числа. Завершите решение проблемы из взятого примера.
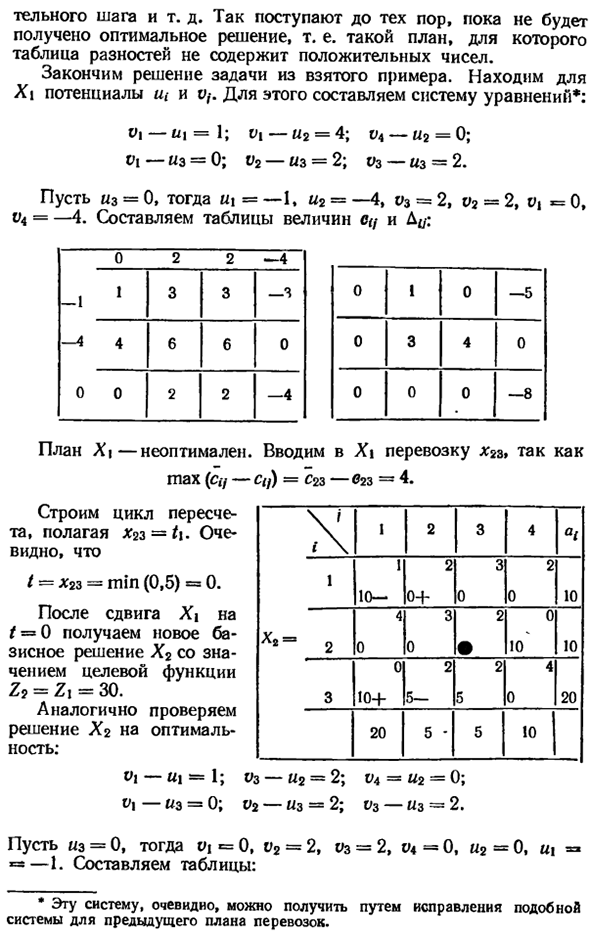
Узнать X \ потенциалы u и ϋ, — для этого построим систему уравнений *: 01-1 / 1 = 1; Vi-U2 = 4; uh-u2 = 0; V \ —U3 = 0; v2-from = 2; t> 3- «s = 2. u = 0, тогда u = -1, u2 = -4, u3 = 2, v2 = 2, vu = 0, ϋ4 = –4. Составляет таблицы значений SC и D #. 1 0 2 2 —4 | L * -4 4 0 0 3 6 2 3 6 2 -3 0 -4 0 0 0 1 3 0 0 4 0 -5 0 -8 План X \ не является оптимальным. Введите в X \ transport # 2z. Максимум (Cq-Cq) = с2з-Фз = 4.
Построить цикл Пересчет в предположении aggs = <ι- Очевидно, что / = x23 = минимум (0,5) = 0 После перехода на shiftι ί = 0 новый Основное решение х2 Значение целевой функции Ζ2 = Ζχ = 30. Проверьте также Решение х2 на Оптимальность: V \ — «v-1; V3-» 2 = 2; v4 = u2 = 0; t / i- «s = 0; v> 2-» s = 2; t / 3-3- «s = 2. = = 0, то ι> ι = 0, υ2 = 2, 0s = 2, sy = 0, m2 = 0, u «5-1. Создайте таблицу. 1 х 1 | X * = 2 3 Я 1 10- 4 0 0 10+ 20 1 2 2 0+ 3 0 2 5 5 3 3 0 2 о 2 5 5 4 2 0 0 10 4 0 10 час 10 10 2_0 *
Эта система явно похожа Система для предыдущего планирования транспортировки. 109 О ■ 0 2 2 0 1 0 0 3 2 2 3 2 2 1 0 0 Опять же, транспортный план Xg не является оптимальным. Введите его Потому что транспорт * i2, maxA = Ai2 = 1. х \? Построить цикл пересчета. = / 2. Очевидно, U = x \ b = = 5.После смены Мы новые действительные базовое решение хз Значение целевой функции Равно Zs = Ζ2-ίΔι2 = = 30-5-1 = ^ 25.
Подтверждение легко хз оптимально Транспортные решения Задача. Вот так Оптимальный план транспортировки Хопт соответствует X Минимальный транспорт стоимость Zm \ n = Z3 = 25. Замечания. Признак неединственности оптимального решения Существование неосновного нулевого типа симплекс-метода Переменные, соответствующие таким различиям Δ, …. вводятся в план транспортировки попеременно Δί; ・
Вы можете найти все лучшие базовые решения для любого транспорта Задача. Так что в этом примере, в дополнение к X3, лучшим решением является Обнаружен методом минимального элемента. Монотонность и конечность потенциального метода. Гадать Уравнение (20). Результат смещения по количеству плана Ho /
Получите новое решение X \ 9, которое стоит доставки Clearly \ явно равен ζ, = ζ + * (Σ «4-Σ ~ * /)> (2Ι) Где tY * Cq и- / £ ~ Q / способствуют изменению стоимости Положительные и отрицательные полуцепные функции соответственно Цикл. Все ячейки в цикле, кроме оригинального xik Cs = vf-u, принадлежащий положительной полуцепи. Замените эти Формула sc через потенциал формулы (21). Я помню.
Две ячейки цикла в любом столбце, или В одной строке, отмеченной противоположным знаком, В результате замены и уменьшения Ζχ = Ζ + 1 (ctk-vk + u) = Z-tbik9 Другими словами, получить выражение (20). Тогда f> 0 И Δ / *> 0, Ζ \ <Ζ, и t = 0 Z \ -для. Продолжение следует Также рассмотрим монотонность потенциального метода и конечность числа Приемлемыми основными решениями транспортных проблем являются: И его конечности.
Открытая модель и математика транспортных задач Модель и рассмотрение транспортных проблем, сформулированных выше Равенство производства и потребления закрыто Модель. На самом деле в большинстве случаев какое-то производство Не обеспечивает продукт или существующие потребности в нем, миллилитр Или за его пределами, то есть ΣЩΦΣbh (22)
Транспортные задачи и их модели Баланс между производством и потреблением, т.е. Условие (22) называется открытым.・ Такие задачи решены Сводя их к закрытым транспортным задачам. Рассмотрим два случая. миллилитр В первом. Σu> Σ6 / Другими словами, объем производства ί = 1 / = 1 Уменьшить общий спрос (обязательно).
Математическая модель Транспортные проблемы в этом случае заключаются в следующем. т н Стоимость портного Ζ = ΣΣsscSh (23) ι «1 / = 1 η При условии ΣXu 0, i = 1, …, m; / = 1, …, n. (26) Чтобы свести проблемы (23) — (26) к закрытым вопросам, Вызывается (n + 1) — Требуются очки виртуального потребления т л *> l-u = Σi * -Σ * / ・
Поддерживает транспорт xit rt + b Задачи для активных потребителей Коэффициент Cbn-n (ί = 1, …, m) равен нулю на 9. здесь Случаи отображаются в таблице транспортных задач Дополнительный столбец. Принять новую (закрытую) модель этого задания Смотри: функция должна быть свернута т н + \ 2 = ΣΣ нетто 111
Под ограничениями н + м ΣXC = ai> i = b ・ -t m ‘> Σ * // = bf, / = 1,2, …, n + l; / = 1 ф =L * i /> 0, / = 1 м; / = 1 н + л, mη Где fc „-i-i = Σβ <-Σ & / ί = 1 / = 1 Возникающая транспортная проблема решается любым известным Метод, например, потенциальный метод. tη Второй случай: Σi * <Σ & / ・ Это транспортная проблема я = 1 / = 1 Случаи описываются моделью: определяют минимальную линейность т н WEΖ = ΣΣ <4 / * ί / <= 1 / = 1 ηt
При условии Σxc = βί »ί = 1, .. ・> ™; Σ ** / ^ by, / = 1, … η; ί = 1ί = 1 xt> 0; i = ■ 1, … m; / = 1 с. Чтобы свести эту проблему к закрытой, (t + 1) -й Фиктивные производственные точки с объемом производства ηha Qrn + l = * Σ & / -Σβί / = 1ί = 1 Если вымышленный, стоимость транспортировки ст / м / (/ == 1 ..-., Для) Трафик Xm + я. / Устанавливается на ноль. В таблице задач В этой ситуации отображается дополнительная строка.
На самом деле математическая модель исходной задачи Нормативный разум. Найти минимальную функцию / l-Hη ζ = ΣΣscchh я = \ / = 1 Под ограничениями ΣXc = β *, ί = 1, …, m + 1; Σ * ι / = bh 1 = ι * · ππ / = Ιι = 1 xt> 0, ί = 1, …, m + 1; / = 1, …, π. Результирующая закрытая транспортная задача Например, это было решено потенциальным методом. Замечания.
Оптимальная переменная xt n + 1> 0 Продукты с раствором, количество x ^ l, j остаются во второй производственной точке. В любом случае окончательное решение Переменная * m_j_lf j, значение этой переменной не соответствует спросу С соответствующими точками потребления.
В заключение, потенциальный метод Единственный способ решить транспортные проблемы. Каждый из этих методов является одним Дело более эффективно * меньше, чем у других друзей. Один из них Метод можно считать реализацией нескольких методов решения. Общая задача линейного программирования. Во многих случаях задачи, которые не связаны с транспортировкой или План транспортировки описывается математической моделью, такой как Транспорт.
В этом случае описывается возможность постановки этой проблемы. По вопросам транспорта. Часто связанные задачи План транспортировки, не соответствующий изложенным выше рамкам Транспортное задание. В таких проблемных моделях добавьте Ограничение или нелинейное выражение с дополнительными соображениями Условия.
Более или менее эффективно для каждого типа такой задачи Как их решить. Так, например, во многих случаях шоссе Пропускная способность поставщика и потребителя ограничена. Если пропускная способность всего шоссе не ясна Должны быть рассмотрены, если это достаточно для выполнения плана Транспортная задача с ограниченной пропускной способностью.
Модель таких задач Отличается от обычного тем, что есть ограничения Учитывайте пропускную способность сети переменного тока всех автомагистралей (/, /). Постановка задачи и модели усложняются наличием промежуточных звеньев Транспортный узел, где обрабатывается груз.
Транспортные проблемные модели будут существенно меняться по мере необходимости Минимизируйте время, необходимое для доставки потребителям. здесь C = (c G A для транспортных вопросов, а не транспортных расходов Учитывать время транспортировки от каждого поставщика до товара (T = / JJ) Для всех потребителей. Предполагается, что время не зависит от объема.
Если громкость равна нулю, то целевая функция задачи Он становится нелинейным и принимает форму max / „-> min. Поэтому для транспортных вопросов, основанных на времени, Выберите приемлемый план на максимально возможное время Максимальный срок выполнения всей перевозки: Как можно ниже.
Для решения этой проблемы был разработан алгоритм [см. 7], На основе сокращения этой проблемы до последовательного решения Некоторые задачи линейного программирования. Многие транспортные проблемы требуют найти Оптимальный план перевозки для нескольких видов товаров вместо одного. Это так называемые многоиндексные задачи.
Так, например, Математическая модель трехиндексной транспортной задачи выглядит следующим образом: Общие транспортные расходы должны быть сведены к минимуму. mηρ ζβΣΣΣcukxijk я = \ / = 1 £ = 1 Все продукты типа k от второго поставщика передаются L Для потребителей ^ xck = aik * * = b 2 t ‘> * = 1, 2 ,. / = л И спрос каждого потребителя каждого вида полностью удовлетворяется T Продукт 5] xtik = bik? Ι = l> 2 l; A = 1, 2ρ;
Очевидное условие jrw> 0, / = I, 2, …, / 77; / = 1, 2, …, η; k = I, 2, …, P По мере увеличения числа индексов проблемы с транспортом становятся все более заметными Увеличьте в размерах и лишите возможности применять методы решения Общая задача линейного программирования. Как правило, в то же время Проблема многоиндексного транспорта все еще недостаточно эффективна Их решение. Есть много других осложнений с транспортными проблемами.
Смотрите также:
Примеры решения задач по математическому программированию
