Оглавление:

Здравствуйте на этой странице я собрала теорию и практику с примерами решения задач по предмету математическое программирование с решением по каждой теме, чтобы вы смогли освежить знания!
| Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу! |
Математическое программирование
Математическое программирование — раздел математики, посвященный теории и методам решения задач поиска экстремумов функций на множестве ограничений. Оно объединяет различные математические методы и дисциплины исследования операций: линейное программирование, нелинейное программирование, динамическое программирование, выпуклое программирование, геометрическое программирование, целочисленное программирование и др.
Использование методов математического программирования
Чтобы использовать методы математического программирования для нахождения оптимального решения, необходимо экономическую проблему записать в виде функций, уравнений, неравенств, цифр и т. д., описывающих характеристики объекта моделирования и взаимосвязи между ними, т. е. составить математическую модель задачи.
Краткая классификация методов математического программирования. Задачи математического программирования в наиболее общем виде классифицируются по следующим признакам.

В случае а) все функциональные связи в системе ограничений и функция цели – линейные функции; наличие нелинейности хотя бы в одном из упомянутых элементов приводит к случаю б).
Примеры задач:
Задача 1.1.
Для изготовления трех видов изделий 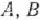 и
и 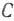 используется токарное, фрезерное, сварочное и шлифовальное оборудование. Затраты времени на обработку одного изделия для каждого из типов оборудования указаны в табл. 1.1. В ней же указал общий фонд рабочего времени каждого из типов используемого оборудования, а также прибыль от реализации одного изделия каждого вида.
используется токарное, фрезерное, сварочное и шлифовальное оборудование. Затраты времени на обработку одного изделия для каждого из типов оборудования указаны в табл. 1.1. В ней же указал общий фонд рабочего времени каждого из типов используемого оборудования, а также прибыль от реализации одного изделия каждого вида.
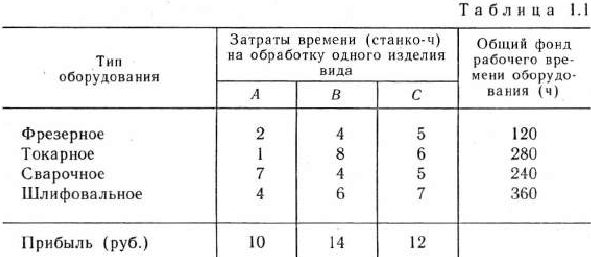
Требуется определить, сколько изделий и какого вида следует изготовить предприятию, чтобы прибыль от их реализации была максимальной. Составить математическую модель задачи.
Решение:
Предположим, что будет изготовлено 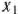 единиц изделий вида
единиц изделий вида 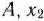 единиц — вида
единиц — вида 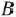 и
и 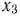 единиц — вида
единиц — вида 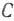 . Тогда для производства такого количества изделий потребуется затратить
. Тогда для производства такого количества изделий потребуется затратить
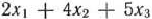
станко-часов фрезерного оборудования.
Так как общий фонд рабочего времени станков данного типа не может превышать 120, то должно выполняться неравенство
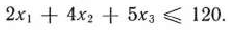
Аналогичные рассуждения относительно возможного использования токарного, сварочного и шлифовального оборудования приведут к следующим неравенствам:
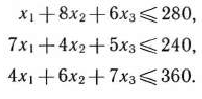
При этом так как количество изготовляемых изделий не может быть отрицательным, то
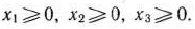
Далее, если будет изготовлено 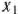 единиц изделий вида
единиц изделий вида 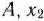 единиц изделий вида
единиц изделий вида 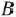 и
и 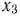 единиц изделий вида
единиц изделий вида 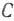 , то прибыль от их реализации составит
, то прибыль от их реализации составит
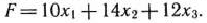
Таким образом, приходим к следующей математической задаче: дана система
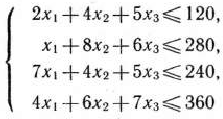
четырех линейных неравенств с тремя неизвестными 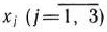 и линейная функция относительно этих же переменных
и линейная функция относительно этих же переменных
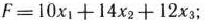
требуется среди всех неотрицательных решений системы неравенств (2) найти такое, при котором функция (3) принимает максимальное значение. Как это сделать, будет показано в дальнейшем.
Линейная функция (3), максимум которой требуется определить, вместе с системой неравенств (2) и условием неотрицательности переменных (1) образуют математическую модель исходной задачи.
Так как функция (3) линейная, а система (2) содержит только линейные неравенства, то задача (1)—(3) является задачей линейного программирования.
Задача 1.2.
Продукцией городского молочного завода являются молоко, кефир и сметана, расфасованные в бутылки. На производство 1 т молока, кефира и сметаны требуется соответственно 1010, 1010 и 9450 кг молока. При этом затраты рабочего времени при разливе 1 т молока и кефира составляют 0,18 и 0,19 ма-шино-ч. На расфасовке 1 т сметаны заняты специальные автоматы в течение 3,25 ч. Всего для производства цельномолочной продукции завод может использовать 136 000 кг молока. Основное оборудование может быть занято в течение 21,4 машино-ч, а автоматы по расфасовке сметаны — в течение 16,25 ч. Прибыль от реализации 1 т молока, кефира и сметаны соответственно равна 30, 22 и 136 руб. Завод должен ежедневно производить не менее 100 т молока, расфасованного в бутылки. На производство другой продукции не имеется никаких ограничений.
Требуется определить, какую продукцию и в каком количестве следует ежедневно изготовлять заводу, чтобы прибыль от ее реализации была максимальной. Составить математическую модель задачи.
Решение:
Предположим, что молочный завод будет ежедневно производить 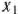 тонн молока,
тонн молока, 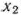 тонн кефира и
тонн кефира и 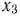 тонн сметаны. Тогда ему для изготовления этой продукции необходимо
тонн сметаны. Тогда ему для изготовления этой продукции необходимо
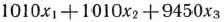
тонн молока.
Так как завод может использовать ежедневно не более 136 000 т молока, то должно выполняться неравенство
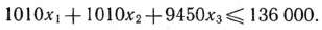
Аналогичные рассуждения, проведенные относительно возможного использования линий разлива цельномолочной продукции и автоматов по расфасовке сметаны, позволяют записать следующие неравенства;
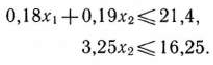
Так как ежедневно должно вырабатываться не менее 100 т молока, то 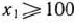 . Далее, по своему экономическому смыслу переменные
. Далее, по своему экономическому смыслу переменные 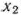 и
и 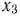 могут принимать только лишь неотрицательные значения:
могут принимать только лишь неотрицательные значения: 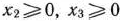 . Общая прибыль от реализации
. Общая прибыль от реализации 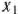 тонн молока,
тонн молока, 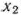 тонн кефира и
тонн кефира и 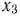 тонн сметаны равна
тонн сметаны равна 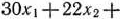
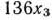 руб. Таким образом, приходим к следующей математической задаче: дана система
руб. Таким образом, приходим к следующей математической задаче: дана система
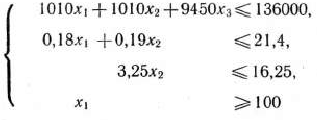
четырех линейных неравенств с тремя неизвестными 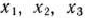 и линейная функция относительно этих же переменных
и линейная функция относительно этих же переменных
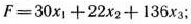
требуется среди всех неотрицательных решений системы неравенств (4) найти такое, при котором функция (5) принимает максимальное значение. Так как система (4) представляет собой совокупность линейных неравенств и функция (5) линейная, то исходная задача является задачей линейного программирования.
Задача 1.3.
На швейной фабрике ткань может быть раскроена несколькими способами для изготовления нужных деталей швейных изделий. Пусть при 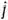 -м варианте раскроя
-м варианте раскроя 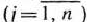 100
100 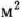 ткани изготовляется
ткани изготовляется 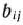 деталей
деталей 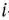 -го вида
-го вида 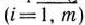 , а величина отходов при данном варианте раскроя равна
, а величина отходов при данном варианте раскроя равна 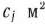 . Зная, что деталей
. Зная, что деталей 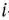 -го вида следует изготовлять
-го вида следует изготовлять 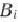 штук, требуется раскроить ткань так, чтобы было получено необходимое количество деталей каждого вида при минимальных общих отходах. Составить математическую модель задачи.
штук, требуется раскроить ткань так, чтобы было получено необходимое количество деталей каждого вида при минимальных общих отходах. Составить математическую модель задачи.
Решение:
Предположим, что по 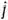 -му варианту раскраивается
-му варианту раскраивается 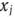 сотен
сотен 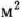 ткани. Поскольку при раскрое 100
ткани. Поскольку при раскрое 100 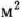 ткани по
ткани по 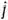 -му варианту получается
-му варианту получается 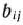 деталей
деталей 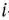 -го вида, по всем вариантам раскроя из используемых тканей будет получено
-го вида, по всем вариантам раскроя из используемых тканей будет получено
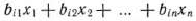
деталей 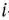 -го вида. Так как должно быть изготовлено
-го вида. Так как должно быть изготовлено 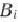 деталей данного вида, то
деталей данного вида, то
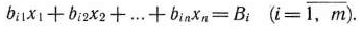
Общая величина отходов по всем вариантам раскроя ткани составит
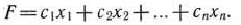
Таким образом, приходим к следующей математической задние: найти минимум функции
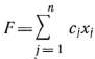
при условии, что ее переменнее удовлетворяют системе уравнений
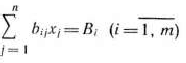
и условию неотрицательности
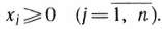
Сформулированная задача является задачей линейного программирования, так как функция (6) линейная, а система (7) содержит только лишь линейные уравнения.
Возможно эта страница вам будет полезна:
| Предмет математическое программирование |
Общая и основная задачи математического программирования
Выше были рассмотрены примеры задач линейного программирования. Во всех этих задачах требовалось найти максимум или минимум линейной функции при условии, что ее переменные принимали неотрицательные значения и удовлетворяли некоторой системы линейных уравнений, содержащей как линейные неравенства, гик и линейные уравнения. Каждая из этих задач является частным случаем общей задачи линейного программирования.
Определение 1.1. Общей задачей линейного программирования называется задача, которая состоит в определении максимального (минимального) значения функции
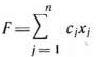
при условиях
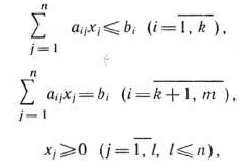
где 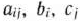 — заданные постоянные величины и
— заданные постоянные величины и 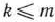 .
.
Определение 1.2. Функция (8) называется целевой функцией (или линейной формой) задачи (8) — (11), а условия (9) — (II) — ограничениями данной задачи,
Определение 1.3. Стандартной (или симметричной) задачей линейного программирования называется задача, которая состоит в определении максимального значения функции (8) при выполнении условий (9) и (II), где 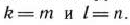
Определение 1.4. Канонической (или основной) задачей линейного программирования называется задача, которая состоит в определении максимального значения функции (8) при выполнении условий (10) и (11), где 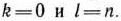
Определение 1.5. Совокупность чисел 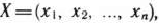 удовлетворяющих ограничениям задачи (9) — (11), называется допустимым решением (или планом).
удовлетворяющих ограничениям задачи (9) — (11), называется допустимым решением (или планом).
Определение 1.6. План 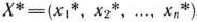 , при котором целевая функция задачи (8) принимает свое максимальное (минимальное) значение, называется оптимальным.
, при котором целевая функция задачи (8) принимает свое максимальное (минимальное) значение, называется оптимальным.
Значение целевой функции (8) при плане 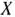 будем обозначать через
будем обозначать через 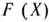 . Следовательно,
. Следовательно, 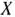 — оптимальный план задачи, если для любого
— оптимальный план задачи, если для любого 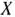 выполняется неравенство
выполняется неравенство 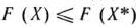 [соответственно
[соответственно 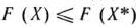 ].
].
Указанные выше три формы задачи линейного программирования эквивалентны в том смысле, что каждая из них с помощью несложных преобразований может быть переписана в форме другой задачи. Это означает, что если имеется способ нахождения решения одной из указанных задач, то тем самым может быть определен оптимальный план любой из трех задач.
Чтобы перейти от одной формы записи задачи линейного программирования к другой, нужно в общем случае уметь, во-первых, сводить задачу минимизации функции к задаче максимизации, во-вторых, переходить от ограничений-неравенств к ог-раничениям-равенствам и наоборот, в-третьих, заменять переменные, которые не подчинены условию неотрицательности.
В том случае, когда требуется найти минимум функции
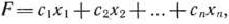
можно перейти к нахождению максимума функции
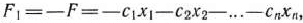
поскольку
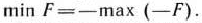
Ограничение-неравенство исходной задачи линейного программирования, имеющее вид 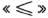 , можно преобразовать в ограничение-равенство добавлением к его левой части дополнительной неотрицательной переменной, а ограничение-неравенство вида
, можно преобразовать в ограничение-равенство добавлением к его левой части дополнительной неотрицательной переменной, а ограничение-неравенство вида 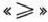 — в ограничение-равенство вычитанием из его левой части дополнительной неотрицательной переменной. Таким образом. ограничение-неравенство
— в ограничение-равенство вычитанием из его левой части дополнительной неотрицательной переменной. Таким образом. ограничение-неравенство
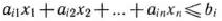
преобразуется в ограничение-равенство
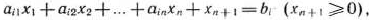
а ограничение-неравенство
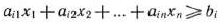
в ограничение-равенство
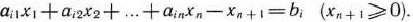
В то же время каждое уравнение системы ограничений
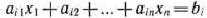
можно записать в виде неравенств:
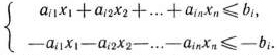
Число вводимых дополнительных неотрицательных переменных при преобразовании ограничений-неравенств в ограничения-равенства равно числу преобразуемых неравенств.
Вводимые дополнительные переменные имеют вполне определенный экономический смысл. Так, если в ограничениях исходной задачи линейного программирования отражается расход и наличие производственных ресурсов, то числовое значение дополнительной переменной в плане задачи, записанной в форме основной, равно объему неиспользуемого соответствующего ресурса.
Отметим, наконец, что если переменная 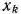 не подчинена условию неотрицательности, то ее следует заменить двумя неотрицательными переменными
не подчинена условию неотрицательности, то ее следует заменить двумя неотрицательными переменными 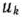 и
и 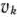 , приняв
, приняв 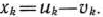
Примеры задач с решением:
- Задача 1.11. Записать в форме основной задачи линейного программирования следующую задачу: найти максимум функции.
- Задача 1.12. Записать задачу, состоящую в минимизации функции
- Задача 1.13. Записать в форме стандартной задачи линейного программирования следующую задачу: найти максимум функции
Свойства основной задачи математического программирования. Геометрическое истолкование задачи математического программирования
Рассмотрим основную задачу линейного программирования. Как было отмечено в § 1.2, она состоит в определении максимального значения функции
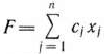
при условиях
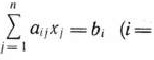
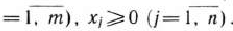
Перепишем эту задачу в векторной форме: найти максимум функции
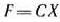
при условиях
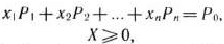
где 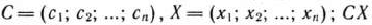 — скалярное произведение;
— скалярное произведение; 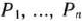 и
и  -мерные вектор-столбцы, составленные из коэффициентов при неизвестных и свободных член ах системы уравнений задачи:
-мерные вектор-столбцы, составленные из коэффициентов при неизвестных и свободных член ах системы уравнений задачи:
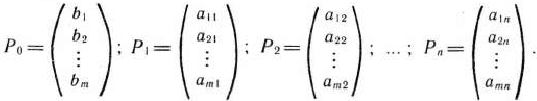
Определение 1.7. План 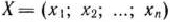 называется опорным планом основной задачи линейного программирования, если система векторов
называется опорным планом основной задачи линейного программирования, если система векторов 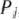 . входящих в разложение (16) с положительными коэффициентами
. входящих в разложение (16) с положительными коэффициентами 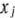 , линейно независима.
, линейно независима.
Так как векторы 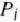 являются
являются 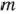 -мерными, то из определения опорного плана следует, что число его положительных компонент не может быть больше, чем
-мерными, то из определения опорного плана следует, что число его положительных компонент не может быть больше, чем 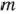 .
.
Определение 1.8. Опорный план называется невырожденным, если он содержит ровно 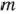 положительных компонент, в противном случае он называется вырожденным.
положительных компонент, в противном случае он называется вырожденным.
Свойства основной задачи линейного программирования (15)—(17) тесным образом связаны со свойствами выпуклых множеств.
Определение 1.9. Пусть
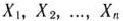
произвольные точки евклидова пространства 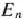 . Выпуклой линейной комбинацией этих точек называется сумма
. Выпуклой линейной комбинацией этих точек называется сумма
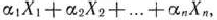
где 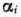 — произвольные неотрицательные числа, сумма которых равна 1:
— произвольные неотрицательные числа, сумма которых равна 1:
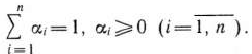
Определение 1.10. Множество называется выпуклым, если вместе с любыми двумя своими точками оно содержит и их произвольную выпуклую линейную комбинацию.
Определение 1.1 1. Точка 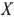 выпуклого множества называется угловой, если она не может быть представлена в виде выпуклой линейной комбинации каких-нибудь двух других различных точек данного множества.
выпуклого множества называется угловой, если она не может быть представлена в виде выпуклой линейной комбинации каких-нибудь двух других различных точек данного множества.
Теорема 1.1. Множество планов основной задачи линейного программирования является выпуклым (если оно не пусто).
Определение 1.12. Непустое множество планов основной задачи линейного программирования называется многогранником решений, а всякая угловая точка многогранника решений — вершиной.
Теорема 1.2. Если основная задача линейного программирования имеет оптимальный план, то максимальное значение целевая функция задачи принимает в одной из вершин многогранника решений. Если максимальное значение целевая функция задачи принимает более чем в одной вершине, то она принимает его во всякой точке, являющейся выпуклой линейной комбинацией этих вершин.
Теорема 1.3. Если система векторов
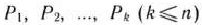
разложении (16) линейно независима и такова, что
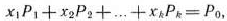
где все 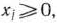 то точка
то точка
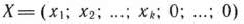
является вершиной многогранника решений.
Теорема 1.4. Если
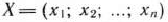
вершина многогранника решений, то векторы 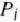 , соответствующие положительным
, соответствующие положительным 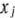 в разложении (16), Линейно независимы.
в разложении (16), Линейно независимы.
Сформулированные теоремы позволяют сделать следующие выводы.
Непустое множество планов основной задачи линейного программирования образует выпуклый многогранник. Каждая вершина этого многогранника определяет опорный план. В одной из вершин многогранника решений (т. е. для одного из опорных планов) значение целевой функции является максимальным (при условии, что функция ограничена сверху на множестве планов). Если максимальное значение функция принимает более чем в одной вершине, то это же значение она принимает в любой точке, являющейся выпуклой линейной комбинацией данных вершин.
Вершину многогранника решений, в которой целевая функция принимает максимальное значение, найти сравнительно просто, если задача, записанная в форме стандартной, содержит не более двух переменных или задача, записанная в форме основной, содержит не более двух свободных переменных, т. е. 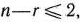 , где
, где 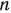 — число переменных,
— число переменных, 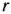 — ранг матрицы, составленной из коэффициентов в системе ограничений задачи.
— ранг матрицы, составленной из коэффициентов в системе ограничений задачи.
Найдем решение задачи, состоящей в определении максимального значения функции
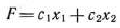
при условиях
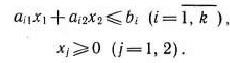
Каждое из неравенств (20), (21) системы ограничений задачи геометрически определяет полуплоскость соответственно с граничными прямыми
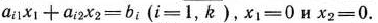
В том случае, если система неравенств (20), (21) совместна, область ее решений есть множество точек, принадлежащих всем указанным полуплоскостям. Так как множество точек пересечения данных полуплоскостей — выпуклое, то областью допустимых решений задачи (19) — (21) является выпуклое множество, которое называется многоугольником решений (введенный ранее термин «многогранник решений» обычно употребляется, если 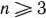 ). Стороны этого многоугольника лежат на прямых, уравнения которых получаются из исходной системы ограничений заменой знаков неравенств на знаки точных равенств.
). Стороны этого многоугольника лежат на прямых, уравнения которых получаются из исходной системы ограничений заменой знаков неравенств на знаки точных равенств.
Таким образом, исходная задача линейного программирования состоит в нахождении такой точки многоугольника решений, в которой целевая функция 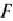 принимает максимальное значение. Эта точка существует тогда, когда многоугольник решений не пуст и на нем целевая функция ограничена сверху. При указанных условиях в одной из вершин многоугольника решений целевая функция принимает максимальное значение. Для определения данной вершины построим линию уровня
принимает максимальное значение. Эта точка существует тогда, когда многоугольник решений не пуст и на нем целевая функция ограничена сверху. При указанных условиях в одной из вершин многоугольника решений целевая функция принимает максимальное значение. Для определения данной вершины построим линию уровня 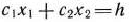 (где
(где 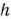 — некоторая постоянная), проходящую через многоугольник решений, и будем передвигать ее в направлении вектора
— некоторая постоянная), проходящую через многоугольник решений, и будем передвигать ее в направлении вектора 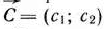 до тех пор, пока она не пройдет через последнюю ее общую точку с многоугольником решений. Координаты указанной точки и определяют оптимальный план данной задачи.
до тех пор, пока она не пройдет через последнюю ее общую точку с многоугольником решений. Координаты указанной точки и определяют оптимальный план данной задачи.
Заканчивая рассмотрение геометрической интерпретации
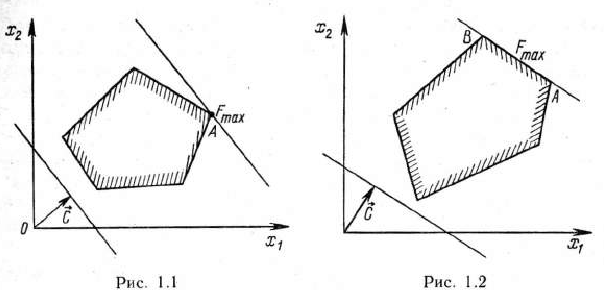
задачи (9)—(21), отметим, что при нахождении ее решения могут встретиться случаи, изображенные на рис. 1.1 —1.4. Рис. 1.1 характеризует такой случай, когда целевая функция принимает максимальное значение в единственной точке 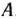 . Из рис. 1.2 видно, что максимальное значение целевая функция принимает в любой точке отрезка
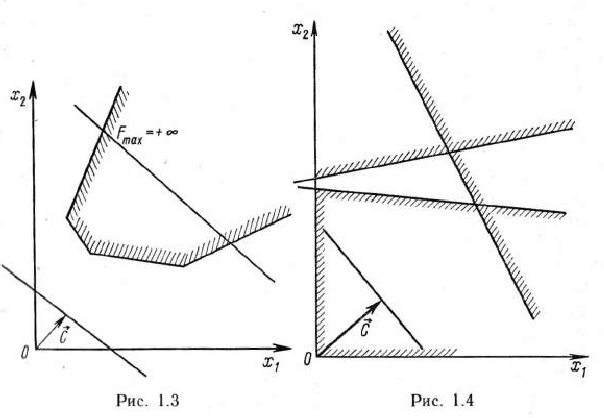
. Из рис. 1.2 видно, что максимальное значение целевая функция принимает в любой точке отрезка 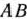 . На рис. 1.3 изображен случай, когда целевая функция не ограничена сверху на множестве допустимых решений, а на рис. 1.4 — случай, когда система ограничений задачи несовместна.
. На рис. 1.3 изображен случай, когда целевая функция не ограничена сверху на множестве допустимых решений, а на рис. 1.4 — случай, когда система ограничений задачи несовместна.
Отметим, что нахождение минимального значения линейной функции при данной системе ограничений отличается от нахождения ее максимального значения при тех же ограничениях лишь
тем, что линия уровня 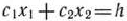 передвигается не в направлении вектора
передвигается не в направлении вектора 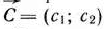 , а в противоположном направлении. Таким образом, отмеченные выше случаи, встречающиеся при нахождении максимального значения целевой функции, имеют место и при определении ее минимального значения.
, а в противоположном направлении. Таким образом, отмеченные выше случаи, встречающиеся при нахождении максимального значения целевой функции, имеют место и при определении ее минимального значения.
Итак, нахождение решения задачи линейного программирования (19) — (21) на основе ее геометрической интерпретации включает следующие этапы:
- Строят прямые, уравнения которых получаются в результате замены в ограничениях (20) и (21) знаков неравенств на знаки точных равенств.
- Находят полуплоскости, определяемые каждым из ограничений задачи.
- Находят многоугольник решений.
- Строят вектор
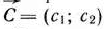 .
. - Строят прямую
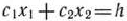 , проходящую через многоугольник решений.
, проходящую через многоугольник решений. - Передвигают прямую
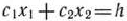 в направлении вектора
в направлении вектора 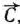 в результате чего либо находят точку (точки), в которой целевая функция принимает максимальное значение, либо устанавливают неограниченность сверху функции на множестве планов.
в результате чего либо находят точку (точки), в которой целевая функция принимает максимальное значение, либо устанавливают неограниченность сверху функции на множестве планов. - Определяют координаты точки максимума функции и вычисляют значение целевой функции в этой точке.
Примеры задач с решением:
- Задача 1.28. Для производства двух видов изделий и предприятие использует три вида сырья. Нормы расхода сырья каждого вида на изготовление единицы продукции данного вида приведены в табл. 1.2. В ней же указаны прибыль от реализации одного изделия каждого вида и общее количество сырья данного вида, которое может быть использовано предприятием.
- Задача 1.29. Найти максимум и минимум функции
- Задача 1.30. Найти максимальное значение функции
- Задача 1.31. Найти решение задачи 1.13, состоящей в определении максимального значения функции
Нахождение решения задачи математического программирования
Решение любой задачи линейного программирования можно найти либо симплексным методом, либо методом искусственного Оазиса. Прежде чем применять один из указанных методов, следует записать исходную задачу в форме основной задачи линейного программирования, если она не имеет такой формы записи.
Симплексный метод
Симплексный метод решения задачи линейного программирования основан на переходе от одного опорного плана к другому, при котором значение целевой функции возрастает (при условии, что данная задача имеет оптимальный план и каждый ее опорный план является невырожденным). Указанный переход возможен, если известен какой-нибудь исходный опорный план. Рассмотрим задачу, для которой этот план можно непосредственно записать.
Пусть требуется найти максимальное значение функции
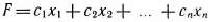
при условиях
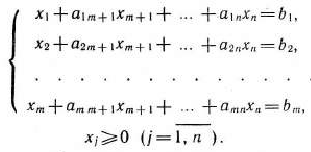
Здесь
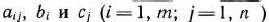
заданные постоянные числа
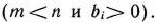
Векторная форма данной задачи имеет следующий вид: найти максимум функции
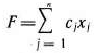
при условиях
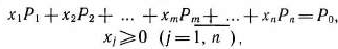
где
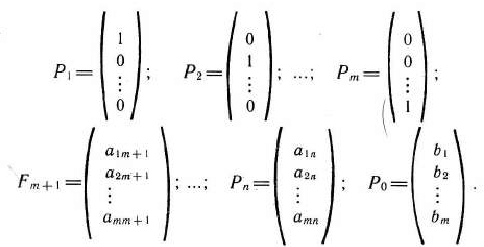
Так как
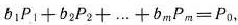
то по определению опорного плана
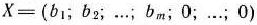
является опорным планом данной задачи (последние  компонент вектора
компонент вектора 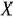 равны нулю). Этот план определяется системой единичных векторов
равны нулю). Этот план определяется системой единичных векторов 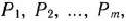 которые образуют базис
которые образуют базис 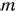 -мерного пространства. Поэтому каждый из векторов
-мерного пространства. Поэтому каждый из векторов 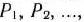
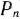 , а также вектор
, а также вектор 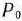 могут быть представлены в виде линейной комбинации векторов данного базиса. Пусть
могут быть представлены в виде линейной комбинации векторов данного базиса. Пусть
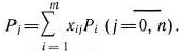
Положим
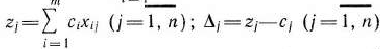
Так как векторы 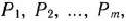 — единичные, то
— единичные, то
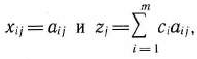
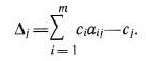
Теорема 1.5 (признак оптимальности опорного плана). Опорный план 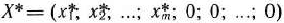 задачи (22)— (24) является оптимальным, если
задачи (22)— (24) является оптимальным, если 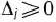 для любого
для любого 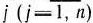 .
.
Теорема 1.6. Если 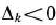 для некоторого
для некоторого 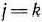 и среды чисел
и среды чисел 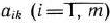 нет положительных
нет положительных 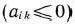 то целевая функция (22) задачи (22)—(24) не ограничена на множестве ее планов.
то целевая функция (22) задачи (22)—(24) не ограничена на множестве ее планов.
Теорема 1.7. Если опорный план 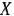 задачи (22) — (24) не вырожден и
задачи (22) — (24) не вырожден и 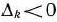 , но среди чисел
, но среди чисел 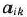 есть положительные (не все
есть положительные (не все 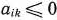 ), то существует опорный план
), то существует опорный план 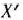 такой, что
такой, что 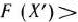
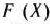 .
.
Сформулированные теоремы позволяют проверить, является ли найденный опорный план оптимальным, и выявить целесообразность перехода к новому опорному плану.
Исследование опорного плана на оптимальность, а также дальнейший вычислительный процесс удобнее вести, если условия задачи и первоначальные данные, полученные после определения исходного опорного плана, записать так, как показано в табл. 1.3.
В столбце 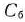 этой таблицы записывают коэффициенты при неизвестных целевой функции, имеющие те же индексы, что и векторы данного базиса.
этой таблицы записывают коэффициенты при неизвестных целевой функции, имеющие те же индексы, что и векторы данного базиса.
В столбце 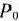 записывают положительные компоненты исходного опорного плана, в нем же в результате вычислений получают положительные компоненты оптимального плана. Столбцы векторов
записывают положительные компоненты исходного опорного плана, в нем же в результате вычислений получают положительные компоненты оптимального плана. Столбцы векторов 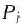 представляют собой коэффициенты разложения этих векторов по векторам данного базиса.
представляют собой коэффициенты разложения этих векторов по векторам данного базиса.
В табл. 1.3 первые 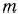 строк определяются исходными данными задачи, а показатели
строк определяются исходными данными задачи, а показатели 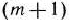 -й строки вычисляют. В этой строке в столбце вектора
-й строки вычисляют. В этой строке в столбце вектора 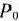 записывают значение целевой функции, которое она принимает при данном опорном плане, а в столбце вектора
записывают значение целевой функции, которое она принимает при данном опорном плане, а в столбце вектора 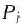 — значение
— значение 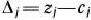 .
.
Значение 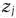 находится как скалярное произведение вектора
находится как скалярное произведение вектора 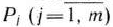 на вектор
на вектор 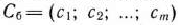 :
:
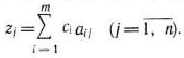
Значение 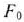 равно скалярному произведению вектора
равно скалярному произведению вектора 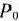 на вектор
на вектор 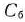 :
:
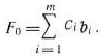
После заполнения таб.п. 1.3 исходный опорный план проверяют на оптимальность. Для этого просматривают элементы 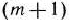 -й строки таблицы. В результате может иметь место один из следующих трех случаев: _
-й строки таблицы. В результате может иметь место один из следующих трех случаев: _
1) 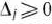 для
для 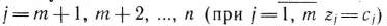 . Поэтому в данном случае числа 0 для всех
. Поэтому в данном случае числа 0 для всех 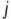 от I до
от I до 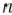 ;
;
2) 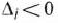 для некоторого
для некоторого 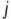 , и все соответствующие этому индексу величины
, и все соответствующие этому индексу величины 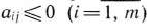 ;
;
3) для некоторых индексов 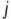 , и для каждого такого
, и для каждого такого 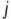 по крайней мере одно из чисел
по крайней мере одно из чисел 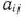 положительно.
положительно.
В первом случае на основании признака оптимальности исходный опорный план является оптимальным. Во втором случае целевая функция не ограничена сверху на множестве планов, а в третьем случае можно перейти от исходного плана к новому опорному плану, при котором значение целевой функции увеличится. Этот переход от одного опорного плана к другому осуществляется исключением из исходного базиса какого-нибудь из векторов и введением в него нового вектора. В качестве вектора, вводимого в базис, можно взять любой из векторов 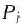 , имеющий индекс
, имеющий индекс 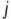 , для которого
, для которого 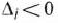 . Пусть, например,
. Пусть, например, 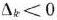 и решено ввести в базис вектор
и решено ввести в базис вектор 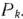 .
.
Для определения вектора, подлежащего исключению из базиса, находят 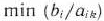 для всех
для всех  . Пусть этот минимум достигается при
. Пусть этот минимум достигается при 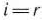 . Тогда из базиса исключают вектор
. Тогда из базиса исключают вектор 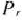 . а число
. а число 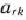 называют разрешающим элементом.
называют разрешающим элементом.
Столбец и строку, на пересечении которых находится разрешающий элемент, называют направляющими.
После выделения направляющей строки и направляющего столбца находят новый опорный план и коэффициенты разложения векторов 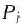 через векторы нового базиса, соответствующего новому опорному плану. Это легко реализовать, если воспользоваться методом Жордана—Гаусса. При этом можно показать, что положительные компоненты нового опорного плана вычисляются по формулам
через векторы нового базиса, соответствующего новому опорному плану. Это легко реализовать, если воспользоваться методом Жордана—Гаусса. При этом можно показать, что положительные компоненты нового опорного плана вычисляются по формулам
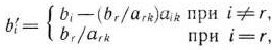
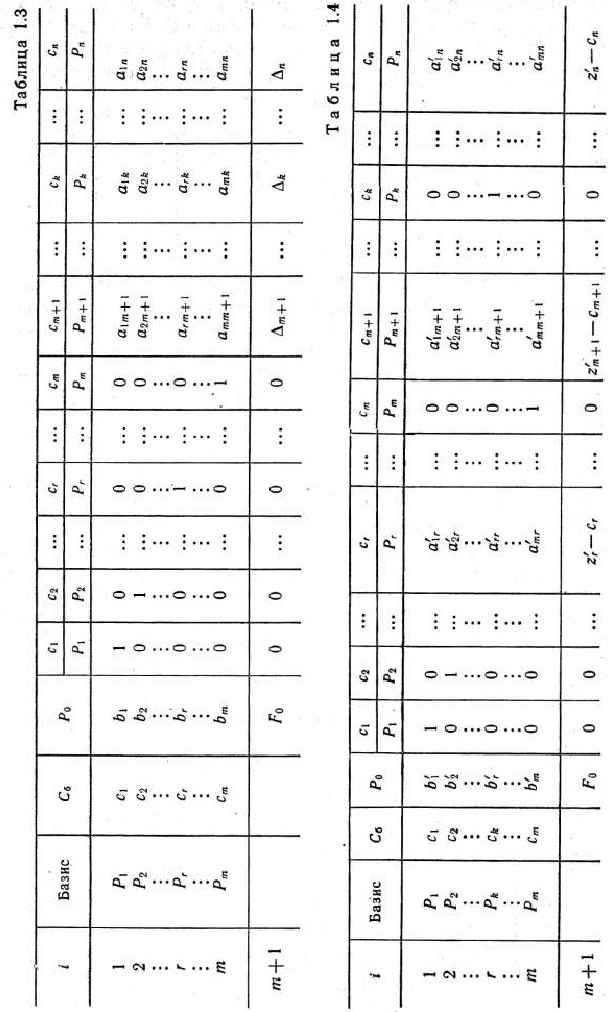
а коэффициенты разложения векторов 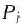 через векторы нового базиса, соответствующего новому опорному плану,— по формулам
через векторы нового базиса, соответствующего новому опорному плану,— по формулам
(26)
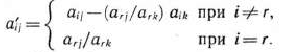
После вычисления 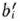 и
и 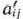 согласно формулам (25) и (26) их значения заносят в табл. 1.4. Элементы
согласно формулам (25) и (26) их значения заносят в табл. 1.4. Элементы 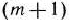 -й строки этой таблицы могут быть вычислены либо по формулам
-й строки этой таблицы могут быть вычислены либо по формулам
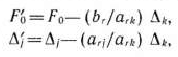
либо на основании их определения.
Наличие двух способов нахождения элементов 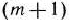 -й строки позволяет осуществлять контроль правильности проводимых вычислений.
-й строки позволяет осуществлять контроль правильности проводимых вычислений.
Из формулы (27) следует, что при переходе от одного опорного плана к другому наиболее целесообразно ввести в базис вектор 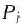 , имеющий индекс
, имеющий индекс 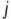 , при котором максимальным по абсолютной величине является число
, при котором максимальным по абсолютной величине является число 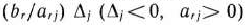 . Однако с целью упрощения вычислительного процесса в дальнейшем будем вектор, вводимый в базис, определять, исходя из максимальной абсолютной величины отрицательных чисел
. Однако с целью упрощения вычислительного процесса в дальнейшем будем вектор, вводимый в базис, определять, исходя из максимальной абсолютной величины отрицательных чисел 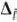 . Если же таких чисел несколько, то в базис будем вводить вектор, имеющий такой же индекс, как и максимальное из чисел
. Если же таких чисел несколько, то в базис будем вводить вектор, имеющий такой же индекс, как и максимальное из чисел 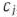 определяемых данными числами
определяемых данными числами 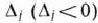 .
.
Итак, переход от одного опорного плана к другому сводится к переходу от одной симплекс-таблицы к другой. Элементы новой симплекс-таблицы можно вычислить как с помощью рекуррентных формул (25) —(28),так и по правилам, непосредственно вытекающим из них. Эти правила состоят в следующем.
В столбцах векторов, входящих в базис, на пересечении строк и столбцов одноименных векторов проставляются единицы, а все остальные элементы данных столбцов полагают равными нулю.
Элементы векторов 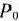 и
и 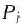 в строке новой симплекс-таблицы, в которой записан вектор, вводимый в базис, получают из элементов этой же строки исходной таблицы делением их на величину разрешающего элемента. В столбце
в строке новой симплекс-таблицы, в которой записан вектор, вводимый в базис, получают из элементов этой же строки исходной таблицы делением их на величину разрешающего элемента. В столбце 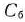 в строке вводимого вектора проставляют величину
в строке вводимого вектора проставляют величину 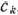 , где
, где 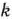 — индекс вводимого вектора.
— индекс вводимого вектора.
Остальные элементы столбцов вектора 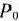 и
и 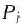 новой симплекс-таблицы вычисляют но правилу треугольника. Для вычисления какого-нибудь из этих элементов находят три числа:
новой симплекс-таблицы вычисляют но правилу треугольника. Для вычисления какого-нибудь из этих элементов находят три числа:
1) число, стоящее в исходной симплекс-таблице на месте искомого элемента новой симплекс-таблицы;
2) число, стоящее в исходной симплекс-таблице на пересечении строки, в которой находится искомый элемент новой симплекс-таблицы, и столбца, соответствующего вектору, вводимому в базис;
3) число, стоящее в новой симплекс-таблице на пересечении столбца, в котором стоит искомый элемент, и строки вновь вводимого в базис вектора (как отмечено выше, эта строка получается из строки исходной симплекс-таблицы делением ее элементов на разрешающий элемент),
Эти три числа образуют своеобразный треугольник, две вершины которого соответствуют числам, находящимся в исходной симплекс-таблице, а третья — числу, находящемуся в новой симплекс-таблице. Для определения искомого элемента новой симплекс-таблицы из первого числа вычитают произведение второго и третьего.
После заполнения новой симплекс-таблицы просматривают элементы 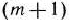 -й строки. Если все
-й строки. Если все 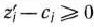 , то новый опорный план является оптимальным. Если же среди указанных чисел имеются отрицательные, то, используя описанную выше последовательность действий, находят новый опорный план. Этот процесс продолжают до тех пор, пока либо не получают оптимальный план задачи, либо не устанавливают ее неразрешимость.
, то новый опорный план является оптимальным. Если же среди указанных чисел имеются отрицательные, то, используя описанную выше последовательность действий, находят новый опорный план. Этот процесс продолжают до тех пор, пока либо не получают оптимальный план задачи, либо не устанавливают ее неразрешимость.
При нахождении решения задачи линейного программирования мы предполагали, что эта задача имеет опорные планы и каждый такой план является невырожденным. Если же задача имеет вырожденные опорные планы, то на одной из итераций одна или несколько переменных опорного плана могут оказаться равными нулю. Таким образом, при переходе от одного опорного плана к другому значение функции может остаться прежним. Более того, возможен случай, когда функция сохраняет свое значение в течение нескольких итераций, а также возможен возврат к первоначальному базису. В последнем случае обычно говорят, что произошло зацикливание. Однако при решении практических задач этот случай встречается очень редко, поэтому мы на нем останавливаться не будем.
Итак, нахождение оптимального плана симплексным методом включает следующие этапы:
- Находят опорный план.
- Составляют симплекс-таблицу.
- Выясняют, имеется ли хотя бы одно отрицательное число
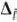 . Если нет, то найденный опорный план оптимален. Если же среди чисел
. Если нет, то найденный опорный план оптимален. Если же среди чисел 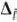 имеются отрицательные, то либо устанавливают неразрешимость задачи, либо переходят к новому опорному плану.
имеются отрицательные, то либо устанавливают неразрешимость задачи, либо переходят к новому опорному плану. - Находят направляющие столбец и строку. Направляющий столбец определяется наибольшим по абсолютной величине отрицательным числом
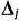 , а направляющая строка — минимальным из отношений компонент столбца вектора
, а направляющая строка — минимальным из отношений компонент столбца вектора 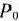 к положительным компонентам направляющего столбца.
к положительным компонентам направляющего столбца. - По формулам (25) — (28) определяют положительные компоненты нового опорного плана, коэффициенты разложения векторов
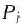 но векторам нового базиса и числа
но векторам нового базиса и числа 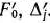 . Все эти числа записываются в новой симплекс-таблице.
. Все эти числа записываются в новой симплекс-таблице. - Проверяют найденный опорный план на оптимальность. Если план не оптимален и необходимо перейти к новому опорному плану, то возвращаются к этапу 4, а в случае получения оптимального плана или установления неразрешимости процесс решения задачи заканчивают.
Примеры задач с решением:
- Задача 1.41. Для изготовления различных изделий и предприятие использует три различных вида сырья. Нормы расхода сырья на производство одного изделия каждого вида, цена одного изделия и , а также общее количество сырья каждого вида, которое может быть использовано предприятием.
- Задача 1.42. Найти максимум функции
- Задача 1.43. Найти решение задачи, состоящей в определении максимального значения функции
Метод искусственного базиса
Для задачи, записанной в форме основной задачи линейного программирования. можно непосредственно указать ее опорный план, если среди векторов 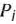 компонентами которых служат коэффициенты при неизвестных в системе уравнений данной задачи, имеется
компонентами которых служат коэффициенты при неизвестных в системе уравнений данной задачи, имеется 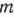 единичных. Однако для многих задач линейного программирования, записанных в форме основной задачи и имеющих опорные планы, среди векторов
единичных. Однако для многих задач линейного программирования, записанных в форме основной задачи и имеющих опорные планы, среди векторов 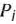 не всегда есть
не всегда есть 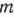 единичных. Рассмотрим такую задачу:
единичных. Рассмотрим такую задачу:
Пусть требуется найти максимум функции
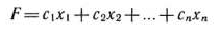
при условиях
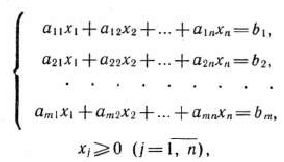
где
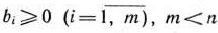
и среди векторов
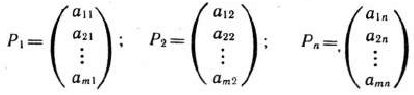
нет 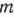 единичных.
единичных.
Определение 1.13. Задача, состоящая в определении максимального значения функции
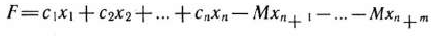
при условиях
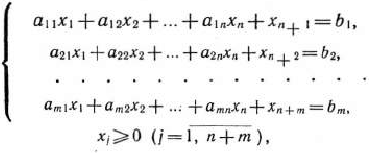
где 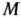 — некоторое достаточно большое положительное число, конкретное значение которого обычно не задается, называется расширенной задачей по отношению к задаче (32) — (34).
— некоторое достаточно большое положительное число, конкретное значение которого обычно не задается, называется расширенной задачей по отношению к задаче (32) — (34).
Расширенная задача имеет опорный план
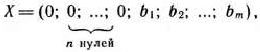
определяется системой единичных векторов
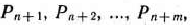
образующих базис 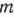 -го векторного пространства, который называется искусственным. Сами векторы, так же как и переменные
-го векторного пространства, который называется искусственным. Сами векторы, так же как и переменные
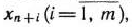
называются искусственными. Так как расширенная задача имеет опорный план, то ее решение может быть найдено симплексным методом.
Теорема 1.8. Если о оптимальном плане
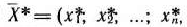
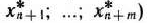
расширенной задачи (35) — (37) значения искусственных переменных
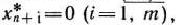
то

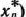
является оптимальным планом задачи (32) — (34),
Таким образом, если в найденном оптимальном плане расширенной задачи, значения искусственных переменных равны нулю, то тем самым получен оптимальный план исходной задачи. Поэтому остановимся более подробно на нахождении решения расширенной задачи.
При опорном плане
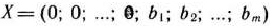
расширенной задачи значение линейной формы есть
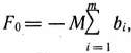
а значения
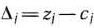
равны
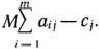
Таким образом, 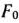 и разности
и разности 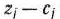 состоят из двух независимых частей, одна из которых зависит от
состоят из двух независимых частей, одна из которых зависит от 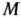 , а другая — нет.
, а другая — нет.
После вычисления 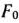 и
и 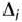 их значения, а также исходные данные расширенной задачи заносят в таблицу, которая содержит на одну строку больше, чем обычная симплексная таблица. При этом в
их значения, а также исходные данные расширенной задачи заносят в таблицу, которая содержит на одну строку больше, чем обычная симплексная таблица. При этом в 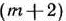 -ю строку помещают коэффициенты при
-ю строку помещают коэффициенты при 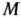 , а в
, а в 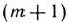 -ю — слагаемые, не содержащие
-ю — слагаемые, не содержащие 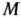 .
.
При переходе от одного опорного плана к другому в базис вводят вектор, соответствующий наибольшему по абсолютной величине отрицательному числу 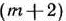 -й строки. Искусственный вектор, исключенный из базиса в результате некоторой итерации, в дальнейшем не имеет смысла вводить ни в один из последующих базисов и, следовательно, преобразование столбцов этого вектора излишне. Однако если нужно найти решение двойственной задачи для данной (о чем будет сказано в $ 1.6), то такое преобразование необходимо. Может случиться так, что в результате некоторой итерации ни один из искусственных векторов из базиса не будет исключен.
-й строки. Искусственный вектор, исключенный из базиса в результате некоторой итерации, в дальнейшем не имеет смысла вводить ни в один из последующих базисов и, следовательно, преобразование столбцов этого вектора излишне. Однако если нужно найти решение двойственной задачи для данной (о чем будет сказано в $ 1.6), то такое преобразование необходимо. Может случиться так, что в результате некоторой итерации ни один из искусственных векторов из базиса не будет исключен.
Пересчет симплекс-таблиц при переходе от одного опорного плана к другому производят по общим правилам симплексного метода.
Итерационный процесс по 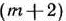 -й строке ведут до тех пор, пока:
-й строке ведут до тех пор, пока:
1) либо все искусственные векторы не будут исключены из базиса;
2) либо не все искусственные векторы исключены, но 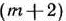 -я строка не содержит больше отрицательных элементов в столбцах векторов
-я строка не содержит больше отрицательных элементов в столбцах векторов

В первом случае базис отвечает некоторому опорному плану исходной задачи и определение ее оптимального плана продолжают по 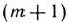 -й строке.
-й строке.
Во втором случае, если элемент, стоящий в 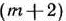 -й строке столбца вектора
-й строке столбца вектора 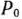 отрицателен, исходная задача не имеет решения; если же он равен нулю, то найденный опорный план исходной задачи является вырожденным и базис содержит по крайней мере один из векторов искусственного базиса.
отрицателен, исходная задача не имеет решения; если же он равен нулю, то найденный опорный план исходной задачи является вырожденным и базис содержит по крайней мере один из векторов искусственного базиса.
Если исходная задача содержит несколько единичных векторов, то их следует включить в искусственный базис.
Следовательно, процесс нахождения решения задачи (32) — (34) методом искусственного базиса включает следующие основные этапы:
- Составляют расширенную задачу (35) — (37).
- Находят опорпый план расширенной задачи.
- С помощью обычных вычислений симплекс метода исключают искусственные векторы из базиса. В результате либо находят опорный план исходной задачи (32) — (34), либо устанавливают ее неразрешимость.
- Используя найденный опорный план задачи (32) — (34), либо находят симплекс-методом оптимальный план исходной задачи, либо устанавливают ее неразрешимость.
Примеры задач с решением:
- Задача 1.44. Найти минимум функции
- Задача 1.45. Найти минимум функции
- Задача 1.46. Найти максимум функции
Модифицированный симплекс-метод
При решении задач линейного программирования симплексным методом осуществлялся упорядоченный переход от одного опорного плана к другому до тех пор, пока либо не была установлена неразрешимость задачи, либо не был найден ее оптимальный план. При этом для определения того, является ли найденный опорный план оптимальным или нет, на каждой из итераций нужно было находить числа
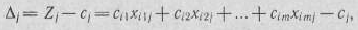
где  — номера базисных векторов, а
— номера базисных векторов, а 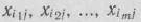 — коэффициенты разложения векторов
— коэффициенты разложения векторов 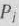 по векторам данного базиса. Все указанные коэффициенты следовало определять на каждой из итераций вычислительного процесса. Эта необходимость отпадает при решении задач линейного программирования модифицированным симплексным методом. В этом случае на каждой из итераций вычисляют вектор
по векторам данного базиса. Все указанные коэффициенты следовало определять на каждой из итераций вычислительного процесса. Эта необходимость отпадает при решении задач линейного программирования модифицированным симплексным методом. В этом случае на каждой из итераций вычисляют вектор
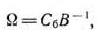
где 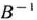 — матрица, обратная матрице
— матрица, обратная матрице 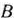 , составленной из компонент векторов данного базиса, а затем находят числа
, составленной из компонент векторов данного базиса, а затем находят числа 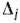 по формуле
по формуле
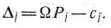
Определим компоненты вектора 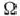 и чисел
и чисел 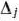 в случае решения основной задачи линейного программирования модифицированным симплекс-методом.
в случае решения основной задачи линейного программирования модифицированным симплекс-методом.
Итак, пусть дана задача линейного программирования, записанная в форме основной задачи, и пусть для нее найден опорный план, который определяется базисом, образованным векторами 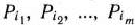 . Следовательно, известна матрица
. Следовательно, известна матрица 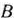 , для которой можно найти обратную матрицу
, для которой можно найти обратную матрицу 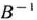 . Дальнейшее вычисление удобнее вести, если их результаты, как и при решении задачи симплексным методом, оформлять в виде таблиц. В этом случае при переходе от одной так называемой основной таблицы к другой используется вспомогательная таблица.
. Дальнейшее вычисление удобнее вести, если их результаты, как и при решении задачи симплексным методом, оформлять в виде таблиц. В этом случае при переходе от одной так называемой основной таблицы к другой используется вспомогательная таблица.
Вспомогательная таблица (табл. 1.21) отличается от обычной симплекс-таблицы тем, что в ней содержатся дополнительные столбцы и строки, в которых соответственно записывают координаты векторов 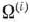 и значения
и значения 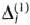 получаемые в процессе нахождения решения задачи.
получаемые в процессе нахождения решения задачи.
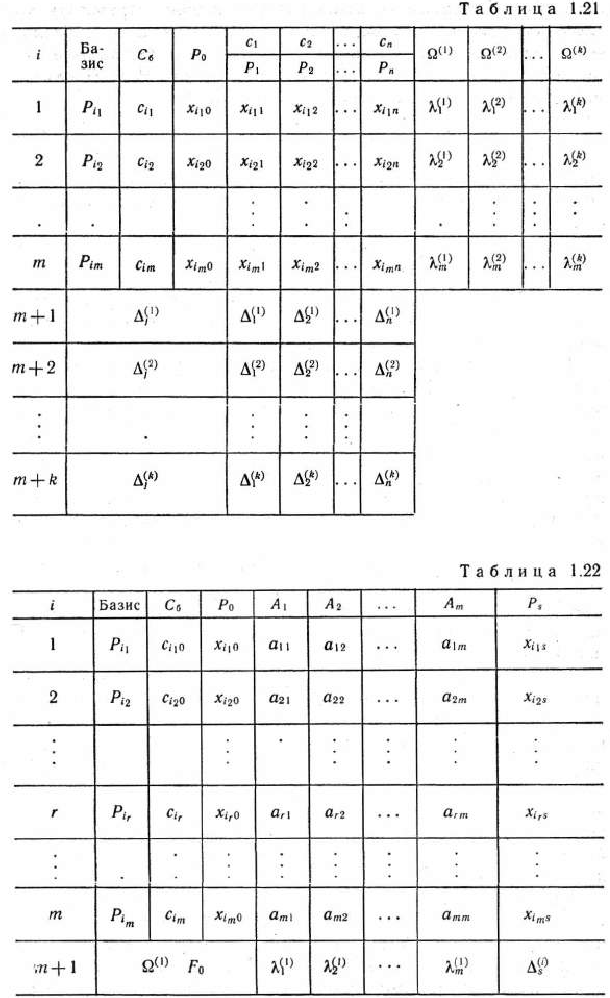
Основная таблица (табл. 1.22) отличается от обычной симплекс-таблицы, во-первых, тем, что вместо столбцов векторов 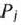 с соответствующими числами
с соответствующими числами 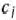 записывают столбцы векторов
записывают столбцы векторов 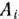 координатами которых являются соответствующие столбцы матрицы
координатами которых являются соответствующие столбцы матрицы 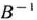 ; во-вторых, в
; во-вторых, в 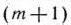 -й строке записывают компоненты векторов
-й строке записывают компоненты векторов 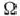 , а не числа
, а не числа 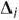 ; в-третьих, табл. 1.22 имеет один дополнительный столбец, в первых
; в-третьих, табл. 1.22 имеет один дополнительный столбец, в первых 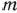 строках которого записывают координаты вектора
строках которого записывают координаты вектора 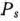 в базисе
в базисе 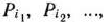
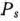 и который было бы целесообразно включить в базис на следующей итерации.
и который было бы целесообразно включить в базис на следующей итерации.
Чтобы определить вектор 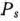 сначала находят вектор
сначала находят вектор 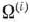 . Его компоненты определяют как скалярное произведение вектора
. Его компоненты определяют как скалярное произведение вектора 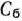 на соответствующие векторы
на соответствующие векторы 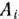 т.е. по формуле (38). Найденные компоненты вектора
т.е. по формуле (38). Найденные компоненты вектора 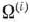 записывают в последней строке табл. 1.22 и в столбце
записывают в последней строке табл. 1.22 и в столбце 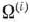 табл. 1.21. После этого по фор-
табл. 1.21. После этого по фор-
муле (39) находят элементы 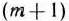 -й строки вспомогательной таблицы. Если среди найденных чисел
-й строки вспомогательной таблицы. Если среди найденных чисел 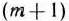 -й строки вспомогательной таблицы нет отрицательных, то исходный опорный план является оптимальным. Если же таковые есть, то либо задача не имеет решения, либо можно перейти к новому опорному плану, при которой значение целевой функции не уменьшится. Для выяснения этого выбирают среди отрицательных чисел
-й строки вспомогательной таблицы нет отрицательных, то исходный опорный план является оптимальным. Если же таковые есть, то либо задача не имеет решения, либо можно перейти к новому опорному плану, при которой значение целевой функции не уменьшится. Для выяснения этого выбирают среди отрицательных чисел 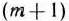 -й строки табл. 1.21 наибольшее по абсолютной величине. В том случае, когда таких чисел несколько, берут какое-нибудь одно. Пусть этим числом является
-й строки табл. 1.21 наибольшее по абсолютной величине. В том случае, когда таких чисел несколько, берут какое-нибудь одно. Пусть этим числом является 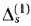 . Тогда последний столбец табл. 1.22 отводят для вектора
. Тогда последний столбец табл. 1.22 отводят для вектора 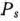 . В первых
. В первых 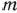 строках этого столбца записывают компоненты вектора
строках этого столбца записывают компоненты вектора 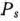 в базисе
в базисе
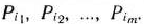
Они получаются в результате умножения матрицы 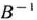 записанной в табл. 1.22, на-вектор
записанной в табл. 1.22, на-вектор 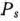 , компоненты которого указаны в табл. 1.21. После определения чисел
, компоненты которого указаны в табл. 1.21. После определения чисел 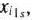
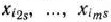 выясняют, имеются ли среди них положительные или нет. Если таких чисел нет, то задача не имеет решения. Если же положительные числа имеются, то переходят к новому опорному плану задачи. Для этого находят
выясняют, имеются ли среди них положительные или нет. Если таких чисел нет, то задача не имеет решения. Если же положительные числа имеются, то переходят к новому опорному плану задачи. Для этого находят
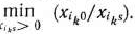
Пусть
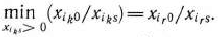
Тогда новый опорный план определяется базисом, получаемым из исходного исключением из него вектора 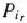 и введением вместо него вектора
и введением вместо него вектора 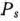 Считая элемент
Считая элемент 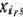 разрешающим, а
разрешающим, а 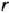 — ю строку и столбец вектора Ps направляющими, переходят к новой основной таблице. Первые
— ю строку и столбец вектора Ps направляющими, переходят к новой основной таблице. Первые 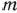 строк столбцов векторов
строк столбцов векторов 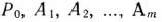 новой таблицы находят по известным правилам перехода от одной симплекс-таблицы к другой, рассмотренным выше. После того как эти элементы определены, находят вектор
новой таблицы находят по известным правилам перехода от одной симплекс-таблицы к другой, рассмотренным выше. После того как эти элементы определены, находят вектор 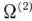 . Компоненты этого вектора записывают как в новой основной таблице, так и в вспомогательной таблице (табл. 1.21). Затем вычисляют числа
. Компоненты этого вектора записывают как в новой основной таблице, так и в вспомогательной таблице (табл. 1.21). Затем вычисляют числа 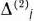 ,и проверяют новый опорный план на оптимальность. Если план не оптимален, то либо устанавливают неразрешимость исходной задачи, либо переходят к новому опорному плану. Продолжая итерационный процесс, после конечного числа шагов либо находят оптимальный план задачи, либо устанавливают ее неразрешимость.
,и проверяют новый опорный план на оптимальность. Если план не оптимален, то либо устанавливают неразрешимость исходной задачи, либо переходят к новому опорному плану. Продолжая итерационный процесс, после конечного числа шагов либо находят оптимальный план задачи, либо устанавливают ее неразрешимость.
Таким образом, процесс нахождения решения задачи модифицированным симплекс-методом включает следующие этапы:
- Находят опорный план задачи.
- Вычисляют матрицу
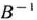 обратную матрице
обратную матрице 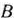 , составленной из компонентов векторов исходного базиса.
, составленной из компонентов векторов исходного базиса. - Находят вектор
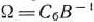 .
. - Вычисляют числа
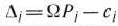 . Если все
. Если все 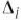 не отрицательны, то исследуемый опорный план является оптимальным. Если же среди чисел
не отрицательны, то исследуемый опорный план является оптимальным. Если же среди чисел 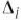 имеются отрицательные, то выбирают среди них наибольшее по абсолютной величине. Пусть это
имеются отрицательные, то выбирают среди них наибольшее по абсолютной величине. Пусть это 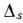 .
. - Вычисляют компоненты вектора
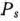 в исходном базисе. Если среди компонент вектора
в исходном базисе. Если среди компонент вектора 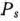 нет положительных, то целевая функция задачи не ограничена на множестве планов. Если же среди компонент вектора
нет положительных, то целевая функция задачи не ограничена на множестве планов. Если же среди компонент вектора 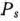 имеются положительные, то переходят к новому опорному плану.
имеются положительные, то переходят к новому опорному плану. - По известным правилам симплекс-метода находят разрешающую строку и вычисляют положительные компоненты нового опорного плана, а также матрицу
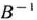 обратную матрице
обратную матрице 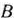 , составленной из компонент векторов нового базиса.
, составленной из компонент векторов нового базиса. - Проверяют новый опорный план на оптимальность и в случае необходимости проводят вычисление начиная с этапа 3.
Примеры задач с решением:
- Задача 1.47. Решить модифицированным симплексным методом задачу 1.41, состоящую в определении максимального значения функции
- Задача 1.48. Найти модифицированным симплекс-методом решение задачи 1.46, состоящей в определении максимального значения функции
Использование пакетов прикладных программ для решения задач математического программирования
В предыдущих параграфах мы рассмотрели методы нахождения решения различных задач линейного программирования. Эти методы определяют алгоритмы решения конкретных задач. Под алгоритмом имеется в виду определенное правило, согласно которому установлен соответствующий порядок выполнения действий над исходными данными в целях получения искомых результатов.
Зная алгоритм решения данной конкретной задачи, можно составить программу ее решения на ЭВМ. Однако во многих случаях, составление такой программы оказывается излишним, поскольку можно воспользоваться существующими пакетами прикладных программ.
Пакет прикладных программ (ППП) представляет собой набор программ, позволяющий решать определенный класс задач и ориентированный на определенный тип машин. Рассмотрим более подробно наиболее часто используемые для нахождения решения задач линейного программирования пакеты прикладных программ: ППП «Линейное программирование-2» (ППП ЛП2) и ППП «Линейное программирование в АСУ» (ППП ЛП АСУ).
- Использование П П П ЛП2 для нахождения решения задач линейного программирования. ППП ЛП2 предназначается для решения задач под управлением дисковой операционной системы ДОС ЕС; при этом используется алгоритм модифицированного симплекс-метода. Применение ППП ЛП2 позволяет находить решения задач линейного программирования с 200 ограничениями на машинах с оперативной памятью 32 К бант и с 1500 ограничениями на машинах с памятью 64 Кбайт. При этом в машину вводятся с перфокарт лишь отличные от нуля исходные данные задачи.
В условиях использования данного пакета прикладных программ появляется возможность одновременно хранить в памяти машины исходные данные нескольких задач, решение каждой из которых может находиться неоднократно с учетом различных изменений в целевой функции и системе ограничений. Кроме того, пользователь ППП ЛП2 может на базе хранящихся в памяти машины различных задач формировать новые задачи.
Наряду с возможностями нахождения решения различных задач использование Г1ПП ЛП2 позволяет проводить анализ полученного решения. Этот анализ может быть самым широким, что определяется пользователем. Например, можно определить, в каких интервалах могут изменяться коэффициенты целевой функции задачи, так чтобы данная задача имела один и тот же оптимальный план. Далее, можно выявить устойчивость оптимального плана задачи относительно изменения свободных членов системы ограничений, а также других параметров задачи.
Чтобы найти решение конкретной задачи линейного программирования с использованием ППП ЛП2, нужно определенным образом подготовить исходные данные задачи, ввести их в ЭВМ и осуществить управление процессом решения задачи, обеспечив выдачу необходимых результатов.
Таким образом, процесс нахождения решения конкретной задачи линейного программирования с использованием ППП ЛП2 включает следующие этапы:
- Составляют математическую модель задачи.
- В соответствии с требованиями ППП ЛП2 элементам математической модели присваивают определенные имена.
- Переписывают математическую модель задачи с учетом введенных имен.
- Составляют матрицу исходных данных.
- Записывают исходные данные на специальном бланке.
- Определяют управляющую программу решения задачи.
- Находят решение задачи на ЭВМ.
- Проводят анализ полученного решения.
Примеры задач с решением:
- Задача 1.65. Используя ППП ЛП2, найти решение задачи 1.41, состоящей в определении плана изготовления изделий А, В и С, обеспечивающего максимальный их выпуск в стоимостном выражении с учетом ограничений на возможное использование сырья трех видов.
- Задача 1.66. На ткацкой фабрике для изготовления трех артикулов ткани используются ткацкие станки двух типов, пряжа и красители. В табл. 1.36 указаны производительность станков каждого типа, нормы расхода пряжи и красителей, цена 1 м ткани данного артикула, а также общий фонд рабочего времени станков каждого типа, имеющиеся в распоряжении фабрики фонды пряжи и красителей и ограничения на возможный выпуск тканей данного артикула.
- Задача 1.67. Машиностроительное предприятие для изготовления четырех видов продукции использует токарное, фрезерное, сверлильное, расточное и шлифовальное оборудование, а также комплектующие изделия. Кроме того, сборка изделий требует выполнения определенных сборочно-наладочных работ. Нормы затрат всех видов ресурсов на изготовление каждого из изделий приведены в табл. 1.39. В этой же таблице указаны наличный фонд каждого из ресурсов, прибыль от реализации единицы продукции данного вида, а также ограничения на возможный выпуск продукции 2-го и 3-вида.
Двойственные задачи математического программирования
I. Прямая и двойственная задачи. Каждой задаче линейного программирования можно определенным образом сопоставить некоторую другую задачу (линейного программирования), называемую двойственной или сопряженной но отношению к исходной или прямой. Дадим определение двойственной задачи по отношению к общей задаче линейного программирования, состоящей в нахождении максимального значения функции
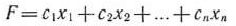
при условиях
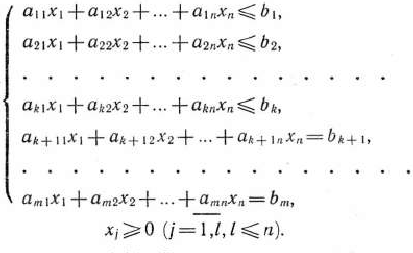
Определение 1.14. Задача, состоящая в нахождении минимального значения функции
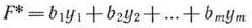
при условиях
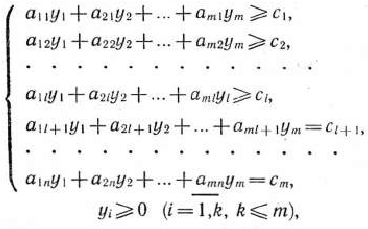
называется двойственной no отношению к задаче (50) — (52).
Задачи (50) — (52) и (53) — (55) образуют пару задач, называемую в линейном программировании двойственной парой.
Сравнивая две сформулированные задачи, видим, что двойственная задача по отношению к исходной составляется согласно следующим правилам:
- Целевая функция исходной задачи (50)—(52) задается на максимум, а целевая функция двойственной (53) — (55) — на минимум.
- Матрица
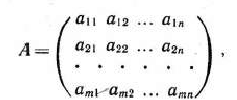
составленная из коэффициентов при неизвестных в системе ограничений (51) исходной задачи (50)—(52), и аналогичная матрица
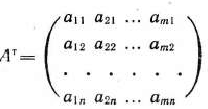
в двойственной задаче (53) — (55) получаются друг из друга транспонированием (т. е. заменой строк столбцами, а столбцов — строками).
- Число переменных в двойственной задаче (53) — (55) равно числу соотношений в системе (51) исходной задачи (50) —(52), а число ограничений в системе (54) двойственной задачи — числу переменных в исходной задаче.
- Коэффициентами при неизвестных в целевой функции (53) двойственной задачи (53) — (55) являются свободные члены в системе (51) исходной задачи (50)—(52), а правыми частями в соотношениях системы (54) двойственной задачи — коэффициенты при неизвестных в целевой функции (50) исходной задачи.
- Если переменная
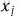 исходной задачи (50) — (52) может принимать только лишь положительные значения, то
исходной задачи (50) — (52) может принимать только лишь положительные значения, то 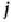 -е условие в системе (54) двойственной задачи (53) — (55) является неравенством вида
-е условие в системе (54) двойственной задачи (53) — (55) является неравенством вида 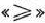 . Если же переменная
. Если же переменная 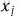 может принимать как положительные, так и отрицательные значения, то
может принимать как положительные, так и отрицательные значения, то 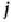 -е соотношение в системе (54) представляет собой уравнение. Аналогичные связи имеют место между ограничениями (51) исходной задачи (50) — (52) и переменными двойственной задачи (53) — (55). Если
-е соотношение в системе (54) представляет собой уравнение. Аналогичные связи имеют место между ограничениями (51) исходной задачи (50) — (52) и переменными двойственной задачи (53) — (55). Если  -е соотношение в системе (51) исходной задачи является неравенством, то
-е соотношение в системе (51) исходной задачи является неравенством, то  -я переменная двойственной задачи
-я переменная двойственной задачи 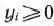 . В противном случае переменная
. В противном случае переменная 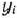 может принимать как положительные, так и отрицательные значения.
может принимать как положительные, так и отрицательные значения.
Двойственные пары задач обычно подразделяют на симметричные и несимметричные. В симметричной паре двойственных задач ограничения (51) прямой задачи и соотношения (54) двойственной задачи являются неравенствами вида 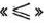 . Таким образом, переменные обеих задач могут принимать только лишь неотрицательные значения.
. Таким образом, переменные обеих задач могут принимать только лишь неотрицательные значения.
Примеры задач с решением:
- Задача 1.77. Составить двойственную задачу по отношению к задаче, состоящей в максимизации функции
- Задача 1.78. Для задачи, состоящей в максимизации функции
- Задача 1.87. Для задачи, состоящей в определении максимального значения функции
- Задача 1.88. Найти решение двойственной пары задач.
- Задача 1.89. Для задачи, состоящей в определении максимального значения функции
Экономическая интерпретация двойственных задач
Экономическую интерпретацию двойственных задач и двойственных оценок рассмотрим на примере.
Пример задачи с решением:
Анализ устойчивости двойственных оценок
Продолжим рассмотрение основной задачи линейного программирования (61)—(63) и двойственной к ней (64). (65).
Предположим, что задача (61) — (63) имеет невырожденные опорные планы и хотя бы один из них является оптимальным.
Максимальное значение целевой функции (61) задачи (61) — (63) будем рассматривать как функцию свободных членов системы линейных уравнений (62):
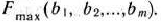
Теорема 1.12. В оптимальном плане двойственной задачи (64), (65) значение переменной 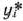 численно равно частной производной функции
численно равно частной производной функции 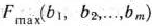 по данному аргументу, т. е.
по данному аргументу, т. е.
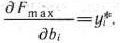
Последнее равенство означает, что изменение значений величин 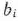 приводит к увеличению или уменьшению
приводит к увеличению или уменьшению 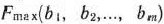 .
.
Это изменение 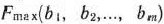 определяется величиной
определяется величиной 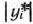 и может быть охарактеризовано лишь тогда, когда при изменении величии
и может быть охарактеризовано лишь тогда, когда при изменении величии 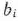 значения переменных
значения переменных 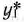 в оптимальном плане соответствующей двойственной задачи (64), (65) остаются неизменными. Поэтому представляет интерес определить такие интервалы изменения каждого из свободных членов системы линейных уравнений (62), в которых оптимальный план двойственной задачи (64), (65) не меняется. Это имеет место для всех тех значений
в оптимальном плане соответствующей двойственной задачи (64), (65) остаются неизменными. Поэтому представляет интерес определить такие интервалы изменения каждого из свободных членов системы линейных уравнений (62), в которых оптимальный план двойственной задачи (64), (65) не меняется. Это имеет место для всех тех значений 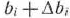 , при которых столбец вектора
, при которых столбец вектора 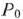 последней симплекс-таблицы решения задачи (61)— (63) не содержит отрицательных чисел, т.е. тогда, когда среди компонент вектора
последней симплекс-таблицы решения задачи (61)— (63) не содержит отрицательных чисел, т.е. тогда, когда среди компонент вектора
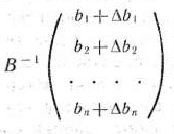
нет отрицательных. Здесь 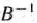 — матрица, обратная матрице
— матрица, обратная матрице 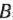 , составленной из компонент векторов базиса, который определяет оптимальный план задачи (61) — (63).
, составленной из компонент векторов базиса, который определяет оптимальный план задачи (61) — (63).
Таким образом, если найдено решение задачи (61) — (63), то нетрудно провести анализ устойчивости двойственных оценок относительно изменений 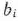 . Это, в свою очередь, позволяет проанализировать устойчивость оптимального плана задачи (64), (65) относительно изменений свободных членов системы линейных уравнений (62), оценить степень влияния изменения bi на максимальное значение целевой функции задачи (61) — (63) и дает возможность определить наиболее целесообразный вариант возможных изменений
. Это, в свою очередь, позволяет проанализировать устойчивость оптимального плана задачи (64), (65) относительно изменений свободных членов системы линейных уравнений (62), оценить степень влияния изменения bi на максимальное значение целевой функции задачи (61) — (63) и дает возможность определить наиболее целесообразный вариант возможных изменений 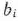 .
.
Пример задачи с решением:
Двойственный симплекс-метод
Двойственный симплекс-метод, как и симплекс-метод, используется при нахождении решения задачи линейного программирования, записанной в форме основной задачи, для которой среди векторов 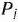 , составленных из коэффициентов при неизвестных в системе уравнений, имеется
, составленных из коэффициентов при неизвестных в системе уравнений, имеется 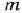 единичных. Вместе с тем двойственный симплекс-метод можно применять при решении задачи линейного программирования, свободные члены системы уравнений которой могут быть любыми числами (при решении задачи симплексным методом эти числа предполагались неотрицательными). Такую задачу и рассмотрим теперь, предварительно предположив, что единичными являются векторы
единичных. Вместе с тем двойственный симплекс-метод можно применять при решении задачи линейного программирования, свободные члены системы уравнений которой могут быть любыми числами (при решении задачи симплексным методом эти числа предполагались неотрицательными). Такую задачу и рассмотрим теперь, предварительно предположив, что единичными являются векторы 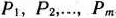 , т.е. рассмотрим задачу, состоящую в определении максимального значения функции
, т.е. рассмотрим задачу, состоящую в определении максимального значения функции
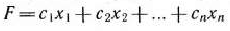
при условиях
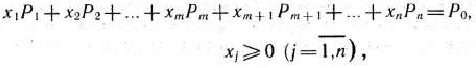
где
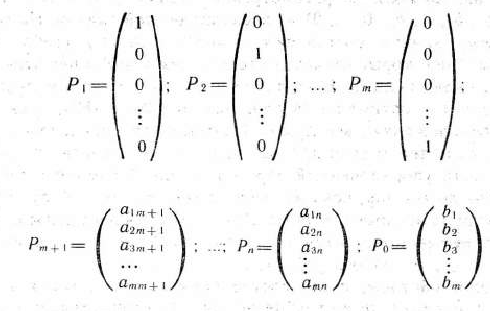
и среди чисел
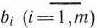
имеются отрицательные.
В данном случае
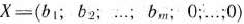
есть решение системы линейных уравнений (81). Однако это решение не является планом задачи (80) — (82), так как среди его компонент имеются отрицательные числа.
Поскольку векторы 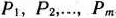 — единичные, каждый из векторов
— единичные, каждый из векторов 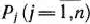 можно представить в виде линейной комбинации данных векторов, причем коэффициентами разложения векторов
можно представить в виде линейной комбинации данных векторов, причем коэффициентами разложения векторов 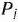 по векторам
по векторам 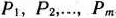 служат числа
служат числа 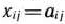
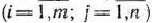 .
.
Таким образом, можно найти
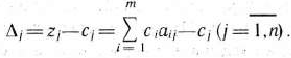
Определение 1.15. Решение
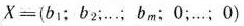
системы линейных уравнений (81), определяемое базисом 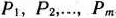 . называется псевдопланом задачи (80) — (82), если
. называется псевдопланом задачи (80) — (82), если 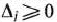 для любого
для любого 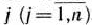 .
.
Теорема 1.13. Если в псевдоплане 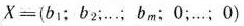 , определяемом базисом
, определяемом базисом 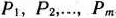 есть хотя бы одно отрицательное число
есть хотя бы одно отрицательное число  такое, что все
такое, что все 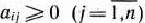 , то задача (80) — (82) вообще не имеет планов.
, то задача (80) — (82) вообще не имеет планов.
Теорема 1,14, Если в псевдоплане 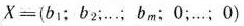 , определяемом базисом
, определяемом базисом 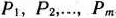 , имеются отрицательные числа
, имеются отрицательные числа  такие, что для любого из них существуют числа
такие, что для любого из них существуют числа 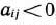 , то можно перейти к новому псевдоплану, при котором значение целевой функции задачи (80) — (82) не уменьшится.
, то можно перейти к новому псевдоплану, при котором значение целевой функции задачи (80) — (82) не уменьшится.
Сформулированные теоремы дают основание для построения алгоритма двойственного симплекс-метода.
Итак, продолжим рассмотрение задачи (80) —(82). Пусть 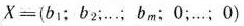 — псевдоплан этой задачи. На основе исходных данных составляют симплекс-таблицу (табл. 1.47), в которой некоторые элементы столбца вектора
— псевдоплан этой задачи. На основе исходных данных составляют симплекс-таблицу (табл. 1.47), в которой некоторые элементы столбца вектора 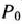 являются отрицательными числами. Если таких чисел нет, то в симплекс-таблице записан оптимальный план задачи (80)—(82), поскольку, по предположению, все
являются отрицательными числами. Если таких чисел нет, то в симплекс-таблице записан оптимальный план задачи (80)—(82), поскольку, по предположению, все 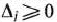 . Поэтому для определения оптимального плана задачи при условии, что он существует, следует произвести упорядоченный переход от одной симплекс-таблицы к другой до тех пор, пока из столбца вектора
. Поэтому для определения оптимального плана задачи при условии, что он существует, следует произвести упорядоченный переход от одной симплекс-таблицы к другой до тех пор, пока из столбца вектора 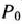 не будут исключены отрицательные элементы. При этом все время должны оставаться неотрицательными все элементы
не будут исключены отрицательные элементы. При этом все время должны оставаться неотрицательными все элементы 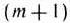 -й строки, т.е.
-й строки, т.е. 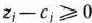 для любого
для любого 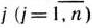 .
.
Таким образом, после составления симплекс-таблицы проверяют, имеются ли в столбце вектора 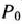 отрицательные числа, Если их нет, то найден оптимальный план исходной задачи. Если же они имеются (что мы и предполагаем), то выбирают наибольшее по абсолютной величине отрицательное число. В том случае, когда таких чисел несколько, берут какое-нибудь одно из них: пусть это число
отрицательные числа, Если их нет, то найден оптимальный план исходной задачи. Если же они имеются (что мы и предполагаем), то выбирают наибольшее по абсолютной величине отрицательное число. В том случае, когда таких чисел несколько, берут какое-нибудь одно из них: пусть это число 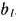 . Выбор этого числа определяет вектор, исключаемый из базиса, т. е. в данном случае из базиса выводится вектор
. Выбор этого числа определяет вектор, исключаемый из базиса, т. е. в данном случае из базиса выводится вектор 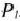 . Чтобы определить, какой вектор следует ввести в базис, находим
. Чтобы определить, какой вектор следует ввести в базис, находим 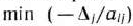 , где
, где 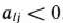 .
.
Пусть это минимальное значение принимается при 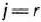 ; тогда в базис вводят вектор
; тогда в базис вводят вектор 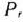 . Число
. Число 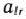 является разрешающим элементом. Переход к новой симплекс-таблице производят по обычным правилам симплексного метода. Итерационный процесс продолжают до тех пор, пока в столбце вектора
является разрешающим элементом. Переход к новой симплекс-таблице производят по обычным правилам симплексного метода. Итерационный процесс продолжают до тех пор, пока в столбце вектора 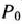 не будет больше отрицательных чисел. При этом находят оптимальный план исходной задачи, а следовательно, и двойственной. Если на некотором шаге окажется, что в
не будет больше отрицательных чисел. При этом находят оптимальный план исходной задачи, а следовательно, и двойственной. Если на некотором шаге окажется, что в 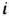 -й строке симплекс-таблицы (табл. 1.47) в столбце вектора
-й строке симплекс-таблицы (табл. 1.47) в столбце вектора 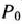 стоит отрицательное число
стоит отрицательное число 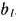 , а среди остальных элементов этой строки нет отрицательных, то исходная задача не имеет решения.
, а среди остальных элементов этой строки нет отрицательных, то исходная задача не имеет решения.
Таким образом, отыскание решения задачи (80) — (£2) двойственным симплекс-методом включает следующие этапы:
- Находят псевдоплан задачи.
- Проверяют этот псевдоплан на оптимальность. Если псевдоплан оптимален, то найдено решение задачи. В противном случае либо устанавливают неразрешимость задачи, либо переходят к новому псевдоплану.
- Выбирают разрешающую строку с помощью определения наибольшего по абсолютной величине отрицательного числа столбца вектора
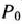 и разрешающий столбец с помощью нахождения наименьшего по абсолютной величине отношения элементов
и разрешающий столбец с помощью нахождения наименьшего по абсолютной величине отношения элементов
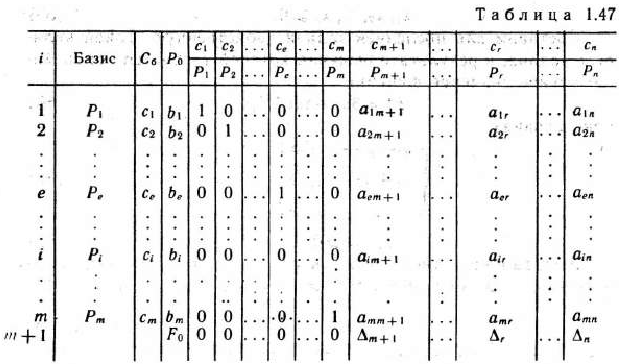
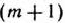 -й строки к соответствующим отрицательным элементам разрешающей строки.
-й строки к соответствующим отрицательным элементам разрешающей строки.
- Находят новый псевдоплан и повторяют все действия начиная с этапа 2.
Примеры задач с решением:
Использование пакетов прикладных программ для после оптимизационного анализа решения задачи
Рассмотренный выше послеоптимизационный анализ решения задачи линейного программирования имеет большое значение для эффективного использования экономико-математических методов в реальных условиях. При этом использование ЕС ЭВМ и ППП позволяет за короткое время и при незначительных затратах находить оптимальный план данной конкретной задачи и проводить послеоптимизационный анализ найденного решения. Это очень важно при принятии управленческих решений, поскольку позволяет для данной конкретной ситуации выбрать наиболее подходящий вариант решения данной задачи.
I. Использование ППП ЛП2 для послеоптимизационного анализа решения задачи. Послеоптимизационный анализ решения задачи в условиях использования ППП ЛП2 реализуется процедурой LPANAI.YSIS. Отчет о нослеоптимизационном анализе выдается в виде таблицы, состоящей из двух частсй. В одной из них приводятся данные анализа для переменных, принявших свои значения на границе области допустимых значений, а в другой — для переменных, принявших значения внутри области их допустимых значений.
В отчете о послеоптимизационном анализе содержится вся информация, имеющаяся в отчетах LPSOLIJTION (см. § 1.5), а также приводятся:
верхнее и нижнее критические значения переменной. Это предельные значения переменной, до которых она может изменяться, так что базис, определяющий данный оптимальный план, содержит одни и те же векторы;
оценки изменения значения целевой функции при единичном увеличении или уменьшении данной переменной. Эти оценки позволяют определить, как изменится значение целевой функции при принудительном изменении значения переменной. Их действие имеет место в интервале от верхнего до нижнего критического значения переменной;
минимальное и максимальное значения коэффициента целевой функции. Эти числа определяют интервал возможных изменений коэффициента целевой функции, для которого оптимальный план остается прежним.
Получение отчета о послеоптимизационном анализе решения задачи с использованием Г1ПП ЛГ12 включает те же основные этапы, что и процесс нахождения решения задачи с использованием данного пакета.
Пример задачи с решением:
Использование П П П ЛП АСУ для послеоитимизационного анализа решения задачи
В условиях использования ППП ЛП АСУ наиболее подробный послеоптимизационный анализ обеспечивается процедурой RANGE. Отчет о послеоптимизацмонном анализе выдается в виде таблицы, включающей четыре секции. Первая секция — СТРОКИ НА ГРАНИЦЕ, вторая секция — СТОЛБЦЫ НА ГРАНИЦЕ, третья секция — СТРОКИ НА ПРОМЕЖУТОЧНОМ УРОВНЕ и четвертая секция — СТОЛБЦЫ НА ПРОМЕЖУТОЧНОМ УРОВНЕ. В секциях содержится вся информация, выдача которой обеспечивается процедурой SOLUTION (см. § 1.5). Кроме того, указываются:
нижняя и верхняя границы переменной, т. е. числа, характеризующие интервал, в котором может изменяться переменная, так что базис, определяющий данный оптимальный план, остается неизменным;
оценка при единичном увеличении (уменьшении) переменной, определяющая возможное изменение значения целевой функции при принудительном изменении значения переменной, принятого в оптимальном плане. Справедливость этого имеет место в интервале, определяемом нижней и верхней границами переменной;
верхнее и нижнее значения коэффициента целевой функции, определяющие интервал возможных значений переменной, для каждого из которых найденный оптимальный план не изменяется;
имена векторов, вводимого в базис и выводимого из базиса, в том случае, если переменная примет значение, не принадлежащее интервалу от нижней до верхней границы переменной; тип переменной, т. е. новое положение переменной. Получение отчета о послеоптимизационном анализе решения задачи включает те же основные этапы, что и процесс нахождения решения задачи с использованием данного пакета.
Пример задачи с решением:
Специальные задачи математического программирования
Транспортная задача
Математическая постановка задачи. Общая постановка транспортной задачи состоит в определении оптимального плана перевозок некоторого однородного груза из 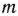 пунктов отправления
пунктов отправления 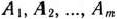 в
в 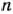 пунктов назначения
пунктов назначения 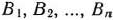 . При этом в качестве критерия оптимальности обычно берется либо минимальная стоимость перевозок всего груза, либо минимальное время его доставки. Рассмотрим транспортную задачу, в качестве критерия оптимальности которой взята минимальная стоимость перевозок всего груза. Обозначим через
. При этом в качестве критерия оптимальности обычно берется либо минимальная стоимость перевозок всего груза, либо минимальное время его доставки. Рассмотрим транспортную задачу, в качестве критерия оптимальности которой взята минимальная стоимость перевозок всего груза. Обозначим через 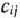 тарифы перевозки единицы груза из
тарифы перевозки единицы груза из 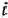 -го пункта отправления в
-го пункта отправления в 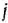 -й пункт назначения, через
-й пункт назначения, через 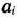 — запасы груза в
— запасы груза в 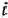 -м пункте отправления, через
-м пункте отправления, через 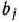 — потребности в грузе в
— потребности в грузе в 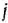 -м пункте назначения, а через
-м пункте назначения, а через 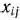 — количество единиц груза, перевозимого из
— количество единиц груза, перевозимого из 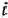 -го пункта отправления в
-го пункта отправления в 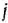 -й пункт назначения. Тогда математическая постановка задачи состоит в определении минимального значения функции
-й пункт назначения. Тогда математическая постановка задачи состоит в определении минимального значения функции
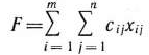
при условиях
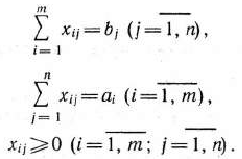
Поскольку переменные 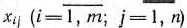 удовлетворяют системам линейных уравнений (2) и (3) и условию неотрицательности (4), обеспечиваются доставка необходимого количества груза в каждый из пунктов назначения, вывоз имеющегося груза из всех пунктов отправления, а также исключаются обратные перевозки.
удовлетворяют системам линейных уравнений (2) и (3) и условию неотрицательности (4), обеспечиваются доставка необходимого количества груза в каждый из пунктов назначения, вывоз имеющегося груза из всех пунктов отправления, а также исключаются обратные перевозки.
Он ре деление 2.1. Всякое неотрицательное решение си стем линейных уравнений (2) и (3), определяемое матрицей 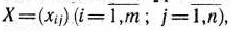 , называется планом транспортной задачи.
, называется планом транспортной задачи.
Определение 2.2. План
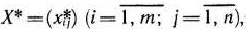
при котором функция (1) принимает свое минимальное значение, называется оптимальным планом транспортной задачи.
Обычно исходные данные транспортной задачи записывают в виде табл. 2.1.
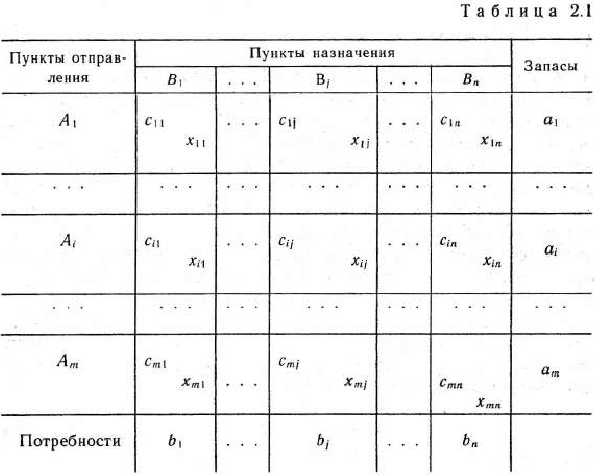
Очевидно, общее наличие груза у поставщиков равно
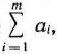
а общая потребность в грузе в пунктах назначения равна
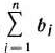
единиц. Если общая потребность в грузе в пунктах назначения равна запасу груза в пунктах отправления, т. е.
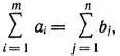
то модель такой транспортной задачи называется закрытой. Если же указанное условие не выполняется, то модель транспортной задачи называется открытой.
Теорема 2.1. Для разрешимости транспортной задачи необходимо и достаточно, чтобы запасы груза в пунктах отправления были равны потребностям в грузе в пунктах назначения, т. е. чтобы выполнялось равенство (5).
В случае превышения запаса над потребностью, т. е.
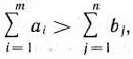
вводится фиктивный 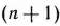 -й пункт назначения с потребностъю
-й пункт назначения с потребностъю
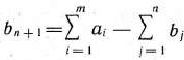
и соответствующие тарифы считаются равными нулю:
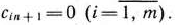
Полученная задача является транспортной задачей, для которой выполняется равенство (5).
Аналогично, при
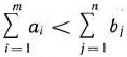
вводится фиктивный 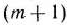 -й пункт отправления с запасом груза
-й пункт отправления с запасом груза
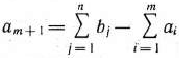
и тарифы полагаются равными нулю:
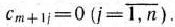
Этим задача сводится к обычной транспортной задаче, из оптимального плана которой получается оптимальный план исходной задачи. В дальнейшем будем рассматривать закрытую модель транспортной задачи. Если же модель конкретной задачи является открытой, то, исходя из сказанного выше, перепишем таблицу условий задачи так, чтобы выполнялось равенство (5).
Число переменных 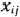 в транспортной задаче с
в транспортной задаче с 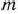 пунктами отправления и
пунктами отправления и 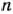 пунктами назначения равно
пунктами назначения равно 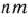 , а число уравнений в системах (2) и (3) равно
, а число уравнений в системах (2) и (3) равно 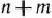 . Так как мы предполагаем, что выполняется условие (5), то число линейно независимых уравнений равно
. Так как мы предполагаем, что выполняется условие (5), то число линейно независимых уравнений равно 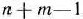 . Следовательно, опорный план транспортной задачи может иметь не более
. Следовательно, опорный план транспортной задачи может иметь не более 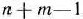 отличных от нуля неизвестных.
отличных от нуля неизвестных.
Если в опорном плане число отличных от нуля компонент равно в точности 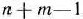 , то план является невырожденным, а если меньше — то вырожденным.
, то план является невырожденным, а если меньше — то вырожденным.
Для определения опорного плана существует несколько методов. Три из них — метод северо-западного угла, метод минимального элемента и метод аппроксимации Фогели — рассматриваются ниже.
Как и для всякой задачи линейного программирования, оптимальный план транспортной задачи является и опорным планом.
Для определения оптимального плана транспортной задачи можно использовать изложенные выше методы. Однако ввиду исключительной практической важности этой задачи и специфики ее ограничений [каждая неизвестная входит лишь в два уравнения систем (2) и (3) и коэффициенты при неизвестных равны единице] для определения оптимального плана транспортной задачи разработаны специальные методы. Два из них — метод потенциалов и метод дифференциальных рент — рассмотрены ниже.
Пример задачи с решением:
Определение опорного плана транспортной задачи
Как и при решении задачи линейного программирования симплексным методом, определение оптимального плана транспортной задачи начинают с нахождения какого-нибудь ее опорного плана. Этот план, как уже отмечалось выше, находят методом северо-западного угла, методом минимального элемента или методом аппроксимации Фогеля. Сущность этих методов состоит в том, что опорный план находят последовательно за 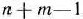 шагов, на каждом из которых в таблице условий задачи заполняют одну клетку, которую называют занятой. Заполнение одной из клеток обеспечивает полностью либо удовлетворение потребности в грузе одного из пунктов назначения (того, в столбце которого находится заполненная клетка), либо вывоз груза из одного из пунктов отправления (из того, в строке которого находится заполняемая клетка).
шагов, на каждом из которых в таблице условий задачи заполняют одну клетку, которую называют занятой. Заполнение одной из клеток обеспечивает полностью либо удовлетворение потребности в грузе одного из пунктов назначения (того, в столбце которого находится заполненная клетка), либо вывоз груза из одного из пунктов отправления (из того, в строке которого находится заполняемая клетка).
В первом случае временно исключают из рассмотрения столбец, содержащий заполненную на данном шаге клетку, и рассматривают задачу, таблица условий которой содержит на один столбец меньше, чем было перед этим шагом, но то же количество строк и соответственно измененные запасы груза в одном из пунктов отправления (в том, за счет запаса которого была удовлетворена потребность в грузе пункта назначения на данном шаге). Во втором случае временно исключают из рассмотрения строку, содержащую заполненную клетку, и считают, что таблица условий имеет на одну строку меньше при неизменном количестве столбцов и при соответствующем изменении потребности в грузе в пункте назначения, в столбце которого находится заполняемая клетка.
После того как проделаны 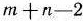 описанных выше шагов, получают задачу с одним пунктом отправления и одним пунктом назначения. При этом останется свободной только одна клетка, а запасы оставшегося пункта отправления будут равны потребностям оставшегося пункта назначения. Заполнив эту клетку, тем самым делают (
описанных выше шагов, получают задачу с одним пунктом отправления и одним пунктом назначения. При этом останется свободной только одна клетка, а запасы оставшегося пункта отправления будут равны потребностям оставшегося пункта назначения. Заполнив эту клетку, тем самым делают (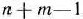 )-й шаг и получают искомый опорный план. Следует заметить, что на некотором шаге (но не на последнем) может оказаться, что потребности очередного пункта назначения равны запасам очередного пункта отправления, В этом случае также временно исключают из рассмотрения либо столбец, либо строку (что-нибудь одно). Таким образом, либо запасы соответствующего пункта отправления, либо потребности данного пункта назначения считают равными нулю. Этот нуль записывают в очередную заполняемую клетку. Указанные выше условия гарантируют получение
)-й шаг и получают искомый опорный план. Следует заметить, что на некотором шаге (но не на последнем) может оказаться, что потребности очередного пункта назначения равны запасам очередного пункта отправления, В этом случае также временно исключают из рассмотрения либо столбец, либо строку (что-нибудь одно). Таким образом, либо запасы соответствующего пункта отправления, либо потребности данного пункта назначения считают равными нулю. Этот нуль записывают в очередную заполняемую клетку. Указанные выше условия гарантируют получение 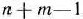 занятых клеток, в которых стоят компоненты опорного плана, что является исходным условием для проверки последнего на оптимальность и нахождения оптимального плана.
занятых клеток, в которых стоят компоненты опорного плана, что является исходным условием для проверки последнего на оптимальность и нахождения оптимального плана.
Метод северо-западного угла. При нахождении опорного плана транспортной задачи методом северо-западного угла на каждом шаге рассматривают первый из оставшихся пунктов отправления и первый из оставшихся пунктов назначения. Заполнение клеток таблицы условий начинается с левой верхней клетки для неизвестного 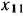 («северо-западный угол») и заканчивается клеткой для неизвестного
(«северо-западный угол») и заканчивается клеткой для неизвестного 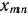 , т. e. идет как бы по диагонали таблицы.
, т. e. идет как бы по диагонали таблицы.
Пример задачи с решением:
Метод минимального элемента
В методе северо-западного угла на каждом шаге потребности первого из оставшихся пунктов назначения удовлетворялись за счет запасов первого из оставшихся пунктов отправления. Очевидно, выбор пунктов назначения и отправления целесообразно производить, ориентируясь на тарифы перевозок, а именно: на каждом шаге следует выбирать какую-нибудь клетку, отвечающую минимальному тарифу (если таких клеток несколько, то следует выбрать любую из них), и рассмотретьпункты назначения и отправления, соответствующие выбранной клетке. Сущность метода минимального элемента и состоит в выборе клетки с минимальным тарифом. Следует отметить, что этот метод, как правило, позволяет найти опорный план транспортной задачи, при котором общая стоимость перевозок груза меньше, чем общая стоимость перевозок при плане, найденном для данной задачи с помощью метода северо-западного угла. Поэтому наиболее целесообразно опорный план транспортной задачи находить методом минимального элемента.
Пример задачи с решением:
Метод аппроксимации Фогеля
При определении оптимального плана транспортной задачи методом аппроксимации Фогеля на каждой итерации по всем столбцам и по всем строкам находят разность между двумя записанными в них минимальными тарифами. Эти разности записывют в специально отведенных для этого строке и столбце в таблице условий задачи. Среди указанных разностей выбирают минимальную. В строке (или в столбце), которой данная разность соответствует, определяют минимальный тариф. Клетку, в которой он записан, заполняют на данной итерации.
Если минимальный тариф одинаков для нескольких клеток данной строки (столбца), то для заполнения выбирают ту клетку, которая расположена в столбце (строке), соответствующем наибольшей разности между двумя минимальными тарифами, находящимися в данном столбце (строке).
Пример задачи с решением:
Определение оптимального плана транспортной задачи
Для определения оптимального плана транспортной задачи разработано несколько методов. Однако наиболее часто используются метод потенциалов и метод дифференциальных рент.
Метод потенциалов. Общий принцип определения оптимального плана транспортной задачи методом потенциалов аналогичен принципу решения задачи линейного программирования симплексным методом, а именно: сначала находят опорный план транспортной задачи, а затем его последовательно улучшают до получения оптимального плана.
Для определения опорного плана транспортной задачи будем пользоваться одним из методов, рассмотренных в предыдущем параграфе. Эти методы гарантируют получение занятых в исходном плане 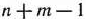 клеток, причем в некоторых из них могут стоять нули. Полученный план следует проверить на оптимальность.
клеток, причем в некоторых из них могут стоять нули. Полученный план следует проверить на оптимальность.
Теорема ‘2.2. Если для некоторого опорного плана 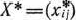
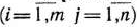 транспортной задачи существуют такие числа
транспортной задачи существуют такие числа
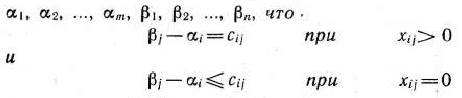
для всех
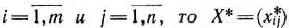
оптимальный план транспортной задачи.
Определение 2.3. Числа 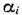 и
и 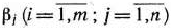 называются потенциалами соответственно пунктов назначения и пунктов потребления.
называются потенциалами соответственно пунктов назначения и пунктов потребления.
Сформулированная теорема позволяет построить алгоритм нахождения решения транспортной задачи. Он состоит в следующем. Пусть одним из рассмотренных выше методов найден опорный план транспортной задачи. Для каждого из пунктов отправленная и назначения определяют потенциалы 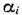 и
и 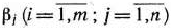 . Эти числа находят из системы уравнений
. Эти числа находят из системы уравнений
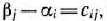
где 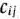 — тарифы, стоящие в заполненных клетках таблицы условий транспортной задачи.
— тарифы, стоящие в заполненных клетках таблицы условий транспортной задачи.
Так как число заполненных клеток равно 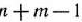 , то система (10) с
, то система (10) с 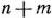 неизвестными содержит
неизвестными содержит 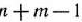 уравнений. Поскольку число неизвестных превышает на единицу число уравнений, одно из неизвестных можно положить равным произвольному числу, например
уравнений. Поскольку число неизвестных превышает на единицу число уравнений, одно из неизвестных можно положить равным произвольному числу, например 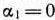 , и найти последовательно из уравнений (10) значения остальных неизвестных. После того как все потенциалы найдены, для каждой из свободных клеток определяют числа
, и найти последовательно из уравнений (10) значения остальных неизвестных. После того как все потенциалы найдены, для каждой из свободных клеток определяют числа 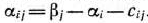
Если среди чисел 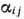 нет положительных, то найденный опорный план является оптимальным. Если же для некоторой свободной клетки
нет положительных, то найденный опорный план является оптимальным. Если же для некоторой свободной клетки 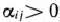 , то исходный опорный план не является оптимальным и необходимо перейти к новому опорному плану. Для этого рассматривают все свободные клетки, для которых
, то исходный опорный план не является оптимальным и необходимо перейти к новому опорному плану. Для этого рассматривают все свободные клетки, для которых 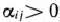 , и среди данных чисел выбирают максимальное. Клетку, которой это число соответствует, следует заполнить.
, и среди данных чисел выбирают максимальное. Клетку, которой это число соответствует, следует заполнить.
Заполняя выбранную клетку, необходимо изменить объемы поставок, записанных в ряде других занятых клеток и связанных с заполненной так называемым циклом.
Оп ределение 2.4. Циклом в таблице условий транспортной задачи называется ломаная линия, вершины которой расположены в занятых клетках таблицы, а звенья—вдоль строк и столбцов, причем в каждой вершине цикла встречается ровно два звена, одно из которых находится в строке, а другое — в столбце.
Если ломаная линия, образующая никл, пересекается, то точки самопересечения не являются вершинами. Примеры некоторых циклов показаны на рис. 2.1.
При правильном построении опорного плана для любой свободной клетки можно построить лишь один цикл. После того как для выбранной свободной клетки он построен, следует перейти к новому опорному плану. Для этого необходимо переместить грузы в пределах клеток, связанных с данной свободной клеткой. Это перемещение производят по следующим правилам:
1) каждой из клеток, связанных циклом с данной свободной клеткой, приписывают определенный знак, причем свободной клетке — знак плюс, а всем остальным клеткам — поочередно знаки минус и плюс (будем называть эти клетки минусовыми и плюсовыми);
2) в данную свободную клетку переносят меньшее из чисел 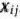 , стоящих в минусовых клетках. Одновременно это число прибавляют к соответствующим числам, стоящим в плюсовых клетках, и вычитают из чисел, стоящих в минусовых клетках. Клетка, которая ранее была свободной, становится занятой, а минусовая клетка, в которой стояло минимальное из чисел
, стоящих в минусовых клетках. Одновременно это число прибавляют к соответствующим числам, стоящим в плюсовых клетках, и вычитают из чисел, стоящих в минусовых клетках. Клетка, которая ранее была свободной, становится занятой, а минусовая клетка, в которой стояло минимальное из чисел 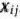 считается свободной.
считается свободной.
В результате указанных выше перемещений грузов в пределах клеток, связанных циклом с данной свободной клеткой, определяют новый опорный план транспортной задачи.
Описанный выше переход от одного опорного плана транспортной задачи к другому ее опорному плану называется сдвигом по циклу пересчета.
Следует отметить, что при сдвиге по циклу пересчета число занятых клеток остается неизменным, а именно остается равным 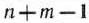 . При этом если в минусовых клетках имеется два (или более) одинаковых числа
. При этом если в минусовых клетках имеется два (или более) одинаковых числа 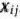 , то освобождают лишь одну из таких клеток, а остальные оставляют занятыми (с нулевыми поставками) .
, то освобождают лишь одну из таких клеток, а остальные оставляют занятыми (с нулевыми поставками) .
Полученный новый опорный план транспортной задачи проверяют на оптимальность. Для этого определяют потенциалы пунктов отправления и назначения и находят числа 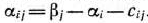 для всех свободных клеток. Если среди этих чисел не окажется положительных, то это свидетельствует о получении оптимального плана. Если же положительные числа имеются, то следует перейти к новому опорному плану. В результате итерационного процесса после конечного числа шагов получают оптимальный план задачи.
для всех свободных клеток. Если среди этих чисел не окажется положительных, то это свидетельствует о получении оптимального плана. Если же положительные числа имеются, то следует перейти к новому опорному плану. В результате итерационного процесса после конечного числа шагов получают оптимальный план задачи.
Из изложенного выше следует, что процесс нахождения решения транспортной задачи методом потенциалов включает следующие этапы:
- Находят опорный план. При этом число заполненных клеток должно быть равным
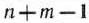 .
. - Находят потенциалы
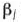 и
и 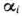 соответственно пунктов назначения и отправления.
соответственно пунктов назначения и отправления. - Для каждой свободной клетки определяют число
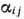 . Если среди чисел
. Если среди чисел 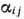 нет положительных, то получен оптимальный план транспортной задачи; если же они имеются, то переходят к новому опорному плану.
нет положительных, то получен оптимальный план транспортной задачи; если же они имеются, то переходят к новому опорному плану. - Среди положительных чисел
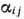 выбирают максимальное, строят для свободной клетки, которой оно соответствует, цикл пересчета и производят сдвиг по циклу пересчета.
выбирают максимальное, строят для свободной клетки, которой оно соответствует, цикл пересчета и производят сдвиг по циклу пересчета. - Полученный опорный план проверяют на оптимальность, т. е. снова повторят все действия начиная с этапа 2.
В заключение отметим, что при определении опорного плана или в процессе решения задачи может быть получен вырожденный опорный план. Чтобы избежать в этом случае зацикливания, следует соответствующие нулевые элементы опорного плана заменить сколь угодно малым положительным числом 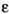 и решать задачу как невырожденную. В оптимальном плане такой задачи необходимо считать
и решать задачу как невырожденную. В оптимальном плане такой задачи необходимо считать 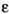 равным нулю.
равным нулю.
Примеры задач с решением:
- Задача 2.17. Для транспортной задачи, исходные данные которой приведены в табл. 2.7, найти оптимальный план
- Задача 2.17.1 Для строительства трех дорог используется гравий из четырех карьеров. Запасы гравия в каждом из карьеров соответственно равны 120, 280 и 160 усл. ед. Потребности в гравии для строительства каждой из дорог соответственно равны 130, 220, 60 и 70 усл. ед. Известны также тарифы перевозок 1 усл. ед. гравия из каждого из карьеров к каждой из строящихся дорог, которые задаются матрицей
Метод дифференциальных рент
Если при определении оптимального плана транспортной задачи методом потенциалов сначала находился какой-нибудь ее опорный план, а затем он последовательно улучшался, то при нахождении решения транспортной задачи методом дифференциальных рент сначала наилучшим образом распределяют между пунктами назначения часть груза (так называемое условно оптимальное распредвление) и на последующих итерациях постепенно уменьшают общую величину нераспределенных поставок. Первоначальный вариант распределения груза определяют следующим образом. В каждом из столбцов таблицы данных транспортной задачи находят минимальный тариф. Найденные числа заключают в кружки, а клетки, в которых стоят указанные числа, заполняют. В них записывают максимально возможные числа. В результате получают некоторое распределение поставок груза в пункты назначения. Это распределение в общем случае не удовлетворяет ограничениям исходной транспортной задачи. Поэтому в результате последующих шагов следует постепенно сокращать нераспределенные поставки груза так, чтобы при этом общая стоимость перевозок оставалась минимальной. Для этого сначала определяют избыточные и недостаточные строки.
Строки, соответствующие поставщикам, запасы которых полностью распределены, а потребности пунктов назначения, связанных сданными потребителями запланированными поставками, не удовлетворены, считаются недостаточными. Эти строки иногда называют также отрицательными. Строки, запасы которых исчерпаны не полностью, считаются избыточными. Иногда их называют также положительными.
После того как определены избыточные и недостаточные строки, для каждого из столбцов находят разности между числом в кружке и ближайшим к нему тарифом, записанным в избыточной строке. Если число в кружке находится в положительной строке, то разность не определяют. Среди полученных чисел находят наименьшее. Это число называется промежуточной рентой. После определения промежуточной ренты переходят к новой таблице. Эта таблица получается из предыдущей таблицы прибавлением к соответствующим тарифам, стоящим в отрицательных строках, промежуточной ренты. Остальные элементы остаются прежними. При этом все клетки новой таблицы считают свободными. После построения новой таблицы начинают заполнение ее клеток. Теперь уже число заполняемых клеток на одну больше, чем на предыдущем этапе. Эта дополнительная клетка находится в столбце, в котором была записана промежуточная рента. Все остальные клетки находятся по одной в каждом из столбцов и в них записаны наименьшие для данного столбца числа, заключенные о кружки. Заключены в кружки и два одинаковых числа, стоящих в столбце, в котором в предыдущей таблице была записана промежуточная рента.
Поскольку в новой таблице число заполняемых клеток больше, чем число столбцов, то при заполнении клеток следует пользоваться специальным правилом, которое состоит в следующем.
Выбирают некоторый столбец (строку), в котором имеется одна клетка с помещенным в ней кружком. Эту клетку заполняют и исключают из рассмотрения данный столбец (строку). После этого берут некоторую строку (столбец), в которой имеется одна клетка с помещенным в ней кружком. Эту клетку заполняют и исключают из рассмотрения данную строку (столбец). Продолжая так, после конечного числа шагов заполняют все клетки, в которых помещены кружки с заключенными в них числами. Если к тому же удается распределить весь груз, имеющийся в пунктах отправления, между пунктами назначения, то получают оптимальный план транспортной задачи. Если же оптимальный план не получен, то переходят к новой таблице. Для этого находят избыточные и недостаточные строки, промежуточную ренту и на основе этого строят новую таблицу. При этом могут возникнуть некоторые затруднения при определении знака строки, когда ее нераспределенный остаток равен нулю. В этом случае строку считают положительной при условии, что вторая заполненная клетка, стоящая в столбце, связанном с данной строкой еще одной заполненной клеткой, расположена в положительной строке.
После конечного числа описанных выше итераций нераспределенный остаток становится равным нулю. В результате получают оптимальный план данной транспортной задачи.
Описанный выше метод решения транспортной задачи имеет более простую логическую схему расчетов, чем рассмотренный выше метод потенциалов. Поэтому в большинстве случаев для нахождения решения конкретных транспортных задач с использованием ЭВМ применяется метод дифференциальных рент.
Пример задачи с решением:
Определение оптимального плана транспортных задач, имеющих некоторые усложнения в их постановке
При нахождении решения ряда конкретных транспортных задач часто бывает необходимо учитывать дополнительные ограничения, которые не встречались выше при рассмотрении простых вариантов данных задач. Остановимся подробнее на некоторых возможных усложнениях в постановках транспортных задач.
При некоторых реальных условиях перевозки груза из определенного пункта отправления 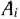 в пункт назначения
в пункт назначения 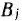 не могут быть осуществлены. Для определения оптимальных планов таких задач предполагают, что тариф перевозки единицы груза из пункта
не могут быть осуществлены. Для определения оптимальных планов таких задач предполагают, что тариф перевозки единицы груза из пункта 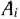 , а пункт
, а пункт 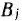 является сколь угодно большой величиной
является сколь угодно большой величиной 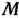 , и при этом условии известными методами находят решение новой транспортной задачи. При таком предположении исключается возможность при оптимальном плане транспортной задачи перевозить груз из пункта
, и при этом условии известными методами находят решение новой транспортной задачи. При таком предположении исключается возможность при оптимальном плане транспортной задачи перевозить груз из пункта 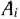 в пункт
в пункт 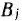 . Такой подход к нахождению решения транспортной задачи называют запрещением перевозок, или блокированием соответствующей клетки таблицы данных задачи.
. Такой подход к нахождению решения транспортной задачи называют запрещением перевозок, или блокированием соответствующей клетки таблицы данных задачи.
- В отдельных транспортных задачах дополнительным условием является обеспечение перевозки по соответствующим маршрутам определенного количества груза. Пусть, например, из пункта отправления
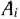 в пункт назначения
в пункт назначения 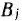 требуется обязательно перевести
требуется обязательно перевести 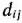 единиц груза. Тогда в клетку таблицы данных транспортной задачи, находящуюся на пересечении строки
единиц груза. Тогда в клетку таблицы данных транспортной задачи, находящуюся на пересечении строки 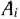 и столбца
и столбца 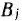 , записывает указанное число
, записывает указанное число 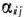 и в дальнейшем эту клетку считают свободной со сколь угодно большим тарифом перевозок
и в дальнейшем эту клетку считают свободной со сколь угодно большим тарифом перевозок 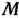 . Для полученной таким образом новой транспортной задачи находят оптимальный план, который определяет оптимальный план исходной задачи.
. Для полученной таким образом новой транспортной задачи находят оптимальный план, который определяет оптимальный план исходной задачи. - Иногда требуется найти решение транспортной задачи, при котором из пункта отправления
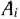 в пункт назначения
в пункт назначения 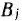 должно быть завезено не менее заданного количества груза
должно быть завезено не менее заданного количества груза 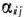 . Для определения оптимального плана такой задачи считают, что запасы пункта
. Для определения оптимального плана такой задачи считают, что запасы пункта 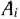 и потребности пункта
и потребности пункта 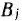 меньше фактических на
меньше фактических на 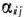 единиц. После этого находят оптимальный план новой транспортной задачи, на основании которого и определяют решение исходной задачи.
единиц. После этого находят оптимальный план новой транспортной задачи, на основании которого и определяют решение исходной задачи. - В некоторых транспортных задачах требуется найти оптимальный план перевозок при условии, что из пункта отправления
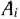 в пункт назначения
в пункт назначения 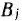 перевозится не более чем
перевозится не более чем 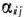 единиц груза, т. е.
единиц груза, т. е.
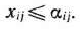
Сформулированную задачу можно решить так. В таблице исходных данных задачи для каждого 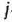 -го ограничения (II) предусматривают дополнительный столбец, т. е. вводят дополнительный пункт назначения. В данном столбце записывают те же тарифы, что к в столбце
-го ограничения (II) предусматривают дополнительный столбец, т. е. вводят дополнительный пункт назначения. В данном столбце записывают те же тарифы, что к в столбце 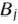 за исключением тарифа, находящегося в
за исключением тарифа, находящегося в 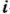 -й строке. В дополнительном столбце в этой строке тариф считают равным некоторому сколь угодно большому числу
-й строке. В дополнительном столбце в этой строке тариф считают равным некоторому сколь угодно большому числу 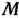 . При этом потребности пункта
. При этом потребности пункта 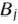 считают равными
считают равными 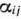 а потребности вновь введенного пункта назначения полагают равными
а потребности вновь введенного пункта назначения полагают равными  . Решение полученной транспортной задачи может быть найдено методом потенциалов, и тем самым будет определен оптимальный план или установлена неразрешимость исходной задачи. Заметим, что исходная транспортная задача разрешима лишь в том случае, когда для нее существует хотя бы один опорный план,
. Решение полученной транспортной задачи может быть найдено методом потенциалов, и тем самым будет определен оптимальный план или установлена неразрешимость исходной задачи. Заметим, что исходная транспортная задача разрешима лишь в том случае, когда для нее существует хотя бы один опорный план,
Приведенную выше задачу можно решить и таким способом. С учетом ограничения (II) по правилу минимального элемента строят опорный план. При этом если величина записываемого на данном шаге в соответствующую клетку числа определяется только ограничением (11), то в последующем из рассмотрения исключают только заполненную клетку. В других случаях из рассмотрения исключают либо строку, либо столбец (что-нибудь одно).
Если в результате составления плана поставок все имеющиеся запасы пунктов отправления распределены и потребности в пунктах назначения удовлетворены, то получен опорный план транспортной задачи.
Если в какой-то строке (а следовательно, и в столбце) остался нераспределенный остаток, равный 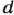 , то вводят дополнительный пункт назначения и дополнительный пункт отправления с потребностями и запасами, равными
, то вводят дополнительный пункт назначения и дополнительный пункт отправления с потребностями и запасами, равными 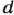 . В клетке, находящейся на пересечении столбца дополнительного пункта назначения и строки дополнительного пункта отправления, тариф считают равным нулю. Во всех остальных клетках данной строки и столбца тарифы полагают равными некоторому сколь угодно большому числу
. В клетке, находящейся на пересечении столбца дополнительного пункта назначения и строки дополнительного пункта отправления, тариф считают равным нулю. Во всех остальных клетках данной строки и столбца тарифы полагают равными некоторому сколь угодно большому числу 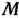 . Полученную в результате этого транспортную задачу решают методом потенциалов. После конечного числа шагов либо устанавливают, что исходная задача не имеет опорного плана, либо находят ее оптимальный план. При этом
. Полученную в результате этого транспортную задачу решают методом потенциалов. После конечного числа шагов либо устанавливают, что исходная задача не имеет опорного плана, либо находят ее оптимальный план. При этом 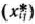 —оптимальный план исходной задачи, если
—оптимальный план исходной задачи, если

Примеры задач с решением:
- Задача 2.29. Найти решение транспортной задачи, исходные данные которой приведены в табл. 2.18, при дополнительных условиях: из в и из в перевозки не могут быть осуществлены, а из в будет завезено 60 ед. груза.
- Задача 2.30. Найти решение транспортной задачи, исходные данные которой приведены в талб. 2.22, при дополнительных условиях: из в должно быть перевезено не менее 50 ед. груза, из в — не менее 60 ед. груза, а из в — не более 40 ед. груза.
Нахождение решения некоторых экономических задач, сводящихся к транспортной
Выше были подробно рассмотрены методы нахождения решения транспортной задачи. Этими же методами может быть также найдено решение многих других задач, которые по своей экономической сущности не связаны с транспортными перевозками. Рассмотрим некоторые из них.
Примеры задач с решением:
- Задача 2.35. На текстильном предприятии имеется три типа ткацких станков. На станках каждого из типов могут вырабатываться четыре вида тканей: миткаль, бязь, ситец и сатин. Производительность каждого станка и себестоимость тканей приведены в табл. 2.25. Учитывая, что фонд рабочего времени каждой из групп ткацких станков соответственно равен 90, 220 и 180 станков, составить такой план их загрузки, при котором общая себестоимость
- Задача 2.36. На пяти токарных станках различных типов можно выполнять пять операций по обработке детали. При этом за каждым из станков может быть закреплена лишь одна операция и одна и та же операция может выполняться только одним станком.
Целочисленные задачи математического программирования
I. Экономическая и геометрическая интерпретация задачи целочисленного программирования. Экстремальная задача, переменные которой принимают лишь целочисленные значения, называется задачей целочисленного программирования.
В математической модели задачи целочисленного программирования как целевая функция, так и функции в системе ограничений могут быть линейными, нелинейными и смешанными. Ограничимся случаем, когда целевая функция и система ограничений задачи являются линейными.
Примеры задач с решением:
- Задача 2.40. В цехе предприятия решено установить дополнительное оборудование, для размещения которого выделено 19/3 площади. На приобретение оборудования предприятие может израсходовать 10 тыс. руб., при этом оно может купить оборудование двух видов. Комплект оборудования I вида стоит 1000 руб., а II вида — 3000 руб. Приобретение одного комплекта оборудования I вида позволяет увеличить выпуск продукции в смену на 2 ед., а одного комплекта оборудования II вида — на 4 ед. Зная, что для установки одного комплекта оборудования I вида требуется 2 площади, а оборудования II вида— 1 площади, определить такой набор дополнительного оборудования, который дает возможность максимально увеличить выпуск продукции.
- Задача 2.41. Для выполнения работ могут быть использованы механизмов. Производительность -механизма при выполнении работы равна . Предполагая, что каждый механизм может быть использован только на одной работе и каждая работа может выполняться только одним механизмом, определить закрепление механизмов за работами, обеспечивающее; максимальную производительность. Построить математическую модель задачи.
Определение оптимального плана задачи целочисленного программирования
Рассмотрим задачи целочисленного программирования, в которых как целевая функция, так и функции в системе ограничений являются линейными. В связи с этим сформулируем основную задачу линейного программирования, в которой переменные могут принимать только целые значения. В общем виде эту задачу можно записать так: найти максимум функции
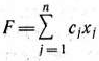
при условиях
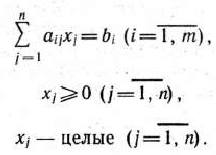
Если найти решение задачи (32) — (35) симплексным методом, то оно может оказаться как целочисленным, так и нет (примером задачи линейного программирования, решение которой всегда является целочисленным, служит транспортная задача). В общем же случае для определения оптимального плана задачи (32) — (35) требуются специальные методы. В настоящее время существует несколько таких методов, из которых наиболее известным является метод Гомори, в основе которого лежит описанный выше симплексный метод.
Метод Гомори
Нахождение решения задачи целочисленного программирования методом Гомори начинают с определения симплексным методом оптимального плана задачи (32) —
(34) без учета целочисленности переменных. После того как этот план найден, просматривают его компоненты. Если среди компонент нет дробных чисел, то найденный план является оптимальным планом задачи целочисленного программирования (32)—
(35). Если же в оптимальном плане задачи (32) — (34) переменная 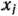 принимает дробное значение, то к системе уравнений (33) добавляют неравенство
принимает дробное значение, то к системе уравнений (33) добавляют неравенство
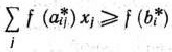
и находят решение задачи (32) — (34), (36).
В неравенстве (36) 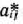 и
и 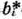 — преобразованные исходные величины
— преобразованные исходные величины 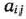 и
и 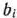 , значения которых взяты из последней симплекс-таблицы, а
, значения которых взяты из последней симплекс-таблицы, а 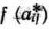 и
и  — дробные части чисел (под дробной частью некоторого числа а понимается наименьшее неотрицательное число
— дробные части чисел (под дробной частью некоторого числа а понимается наименьшее неотрицательное число 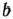 такое, что разность между
такое, что разность между 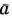 и
и 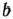 есть целое). Если в оптимальном плане задачи (32) —(34) дробные значения принимают несколько переменных, то дополнительное неравенство (36) определяется наибольшей дробной частью.
есть целое). Если в оптимальном плане задачи (32) —(34) дробные значения принимают несколько переменных, то дополнительное неравенство (36) определяется наибольшей дробной частью.
Если в найденном плане задачи (32)—(34), (36) переменные принимают дробные значения, то снова добавляют одно дополнительное ограничение и процесс вычислений повторяют. Проводя конечное число итераций, либо получают оптимальный план задачи целочисленного программирования (32) — (35), либо устанавливают ее неразрешимость.
Если требование целочисленности (35) относится лишь к некоторым переменным, то такие задачи называются частично целочисленными. Их решение также находят последовательным решением задач, каждая из которых получается из предыдущей с помощью введения дополнительного ограничения. В этом случае такое ограничение имеет вид
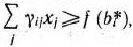
где 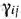 определяются из следующих соотношений:
определяются из следующих соотношений:
1) для 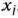 которые могут принимать нецелочисленные значения,
которые могут принимать нецелочисленные значения,
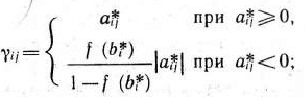
2) для 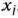 , которые могут принимать только целочисленные значения,
, которые могут принимать только целочисленные значения,
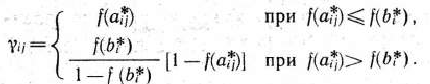
Из изложенного выше следует, что процесс определения оптимального плана задачи целочисленного программирования методом Гомори включает следующие основные этапы:
- Используя симплексный метод, находят решение задачи (32) —(34) без учета требования целочисленности переменных.
- Составляют дополнительное ограничение для переменной, которая в оптимальном плане задачи (32) —(34) имеет максимальное дробное значение, а в оптимальном плане задачи (32) — (35) должна быть целочисленной.
- Используя двойственный симплекс-метод, находят решение задачи, получающейся из задачи (32) — (34) в результате присоединения дополнительного ограничения.
- В случае необходимости составляют еще одно дополнительное ограничение и продолжают итерационный процесс до получения оптимального плана задачи (32) —(35) или установления ее неразрешимости.
Примеры задач с решением:
- Задача 2.49. Методом Гомори найти максимальное значение функции
- Задача 2.50. Методом Гомори найти решение задачи, состоящей в определении максимального значения функции
Использование ППП ЛП АСУ для решения задач целочисленного программирования
Как уже отмечалось выше, решение задачи целочисленного программирования может быть найдено с использованием ППП ЛП АСУ. При этом число переменных решаемой задачи при оперативной памяти, равной 1024 Кбайт, не должно превышать 4095, Для решения задач целочисленного программирования используется метод ветвей и границ.
Процесс нахождения решения задачи целочисленного программирования с использованием ППП ЛП АСУ включает те же основные этапы, что и при нахождении решения задачи линейного программирования с использованием данного пакета. Однако здесь имеется некоторая специфика в записи исходных данных и в управляющей программе. Основной особенностью записи целочисленных переменных является то, что в секции COLUMNS запись каждого набора целочисленных переменных начинается и заканчивается специальными маркерами, а в секции BOUNDS обязательным является задание верхних границ целочисленных переменных. Эти границы определяются исходя из условий каждой конкретной задачи.
В начале каждого набора целочисленных переменных в поле 2 записывается присвоенное имя начала набора переменных (оно может быть любым и должно отличаться от других используемых маркеров и имен), в поле 3 указывается ключевое слово »MARKER7, а в поле 5 записывается маркер начала набора переменных ‘INTORG’. Все остальные поля остаются пустыми.
После записи данного набора целочисленных переменных в поле 2 указывается имя конца набора переменных, в голе 3 записывается ключевое слово ‘MARKER’, а в поле 5 указывается маркер конца набора ‘INTEND^.
Пример задачи с решением:
Задачи параметрического программирования
Экономическая и геометрическая интерпретации задачи параметрического программирования. Во многих задачах математического программирования исходные данные зависят от некоторого параметра. Такие задачи называются задачами параметрического программирования.
Рассмотрим зависимость исходных данных от некоторого параметра применительно к основной задаче линейного программирования.
Задача, в которой коэффициенты целевой функции линейно зависят от параметра 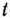 , заключается в нахождении для каждого значения параметра
, заключается в нахождении для каждого значения параметра 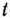 из промежутка его изменения
из промежутка его изменения 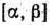 максимального значения функции
максимального значения функции
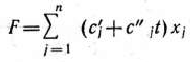
при условиях
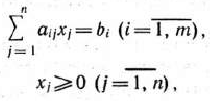
где 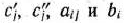 —заданные постоянные числа.
—заданные постоянные числа.
Если от параметра 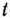 линейно зависят свободные члены системы ограничений, то задача состоит в нахождении для каждого значения параметра
линейно зависят свободные члены системы ограничений, то задача состоит в нахождении для каждого значения параметра  из промежутка его изменения
из промежутка его изменения 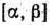 максимального значения линейной функции
максимального значения линейной функции
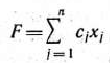
при условиях
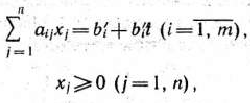
где 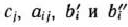 — заданные постоянные числа.
— заданные постоянные числа.
В том случае, когда от параметра 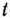 линейно зависят как коэффициенты целевой функции, так и свободные члены системы ограничений, задача состоит в нахождении для каждого значения параметра
линейно зависят как коэффициенты целевой функции, так и свободные члены системы ограничений, задача состоит в нахождении для каждого значения параметра 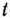 из промежутка его изменения
из промежутка его изменения 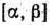 максимального значения функции
максимального значения функции
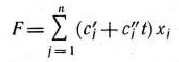
при условиях
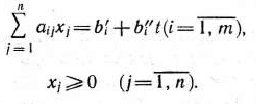
Обобщением этих задач является общая задача параметрического программирования, в которой от параметра 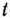 линейно зависят коэффициенты при неизвестных в целевой функции, коэффициенты при неизвестных в системе уравнений и свободные члены системы уравнений. Она заключается в следующем. Для каждого значения параметра
линейно зависят коэффициенты при неизвестных в целевой функции, коэффициенты при неизвестных в системе уравнений и свободные члены системы уравнений. Она заключается в следующем. Для каждого значения параметра 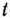 из некоторого промежутка его изменения
из некоторого промежутка его изменения 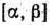 требуется найти максимальное значение функции
требуется найти максимальное значение функции
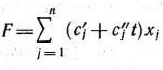
при условиях
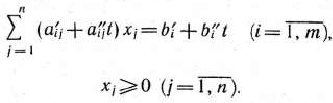
Решение сформулированных задач можно найти методами линейного программирования, о чем более подробно будет сказано в дальнейшем. Рассмотрим геометрическую интерпретацию задач параметрического программирования, остановившись более подробно на задаче (57) — (59). Предположим, что множество неотрицательных решений системы линейных уравнений (58) (многогранник решений) не пусто и включает более чем одну точку. Тогда исходная задача состоит в определении при каждом значении параметра 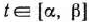 такой точки многогранника решений, в которой функция (57) принимает максимальное значение. Чтобы найти указанную точку, будем считать
такой точки многогранника решений, в которой функция (57) принимает максимальное значение. Чтобы найти указанную точку, будем считать  и, используя геометрическую интерпретацию, находим решение полученной задачи линейного программирования (57)—(59), т.е. либо определяем вершину многогранника решений, в которой функция (57) имеет максимальное значение, либо устанавливаем, что при данном значении
и, используя геометрическую интерпретацию, находим решение полученной задачи линейного программирования (57)—(59), т.е. либо определяем вершину многогранника решений, в которой функция (57) имеет максимальное значение, либо устанавливаем, что при данном значении 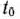 задача неразрешима. После того как найдена тонка, в которой при
задача неразрешима. После того как найдена тонка, в которой при  функция (57) принимает максимальное значение, ищется множество значений
функция (57) принимает максимальное значение, ищется множество значений 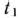 для которых координаты указанной точки определяют оптимальный план задачи (57)—(59). Найденные значения параметра
для которых координаты указанной точки определяют оптимальный план задачи (57)—(59). Найденные значения параметра 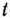 исключаются из рассмотрения и берется некоторое новое значение
исключаются из рассмотрения и берется некоторое новое значение 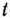 , принадлежащее промежутку
, принадлежащее промежутку 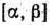 . Для выбранного значения параметра
. Для выбранного значения параметра 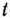 определяется оптимальный план полученной задачи или устанавливается ее неразрешимость. После этого находится отрезок изменения параметра
определяется оптимальный план полученной задачи или устанавливается ее неразрешимость. После этого находится отрезок изменения параметра 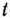 , принадлежащий промежутку
, принадлежащий промежутку 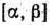 , для которого найденная точка определяет оптимальный план или для которого задача неразрешима. В результате после конечного числа шагов для каждого значения параметра
, для которого найденная точка определяет оптимальный план или для которого задача неразрешима. В результате после конечного числа шагов для каждого значения параметра 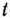 из промежутка
из промежутка 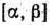 либо находится оптимальный план, либо устанавливается неразрешимость задачи.
либо находится оптимальный план, либо устанавливается неразрешимость задачи.
Пример задачи с решением:
Нахождение решения задачи параметрического программирования
Решение задачи, целевая функция которой содержит параметр. Продолжим рассмотрение задачи (57) —(59). Считая значение параметра 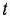 равным некоторому числу
равным некоторому числу 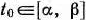 , находим симплексным методом или методом искусственного базиса решение полученной таким образом задачи линейного программирования.
, находим симплексным методом или методом искусственного базиса решение полученной таким образом задачи линейного программирования.
В результате при данном значении 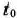 либо найдем оптимальный план задачи (57) — (59), либо установим ее неразрешимость. В первом случае, используя элементы
либо найдем оптимальный план задачи (57) — (59), либо установим ее неразрешимость. В первом случае, используя элементы 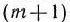 -й строки последней симплекс-таблицы решения задачи, в которой записаны числа
-й строки последней симплекс-таблицы решения задачи, в которой записаны числа 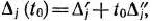 находим:
находим:
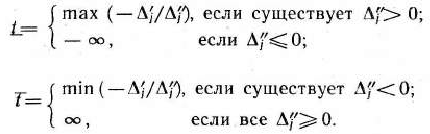
Для всех 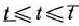 задача (57) — (59) имеет один и тот же оптимальный план, что и при
задача (57) — (59) имеет один и тот же оптимальный план, что и при 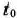 .
.
В том случае, если задача (57) — (59) при 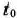 неразрешима, в
неразрешима, в 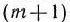 -й строке последней симплекс-таблицы ее решения имеется число
-й строке последней симплекс-таблицы ее решения имеется число 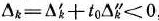 где
где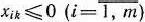 . Тогда:
. Тогда:
1) если 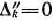 , то задача (57) — (59) неразрешима для любого
, то задача (57) — (59) неразрешима для любого 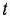 ;
;
2) если 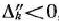 , то задача (57)—(59) неразрешима для всех
, то задача (57)—(59) неразрешима для всех 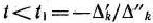 ;
;
3) если 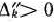 , то задача (57) —(59) неразрешима для всех
, то задача (57) —(59) неразрешима для всех  .
.
Определив все значения параметра 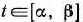 , для которых
, для которых
задача (57) — (59) имеет один и тот же оптимальный план или для которых задача неразрешима, получаем промежуток изменения параметра 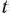 , который исключаем из рассмотрения. Снова полагаем значение параметра
, который исключаем из рассмотрения. Снова полагаем значение параметра 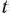 равным некоторому числу, принадлежащему промежутку
равным некоторому числу, принадлежащему промежутку 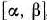 , и находим решение полученной задачи.
, и находим решение полученной задачи.
После конечного числа итераций определяется либо промежуток. в котором для всех значений параметра задача имеет один и тот же оптимальный план, либо промежуток, в котором для всех значений параметра задача не имеет решения.
Итак, процесс нахождения решения задачи (57)—(59) включает следующие этапы:
- Считая значение параметра
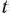 равным некоторому числу
равным некоторому числу 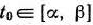 , находят оптимальный план
, находят оптимальный план 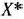 или устанавливают неразрешимость полученной задачи линейного программирования.
или устанавливают неразрешимость полученной задачи линейного программирования. - Определяют множество значений параметра
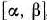 , для которых найденный оптимальный план является оптимальным или задача неразрешима. Эти значения параметра исключают из рассмотрения.
, для которых найденный оптимальный план является оптимальным или задача неразрешима. Эти значения параметра исключают из рассмотрения. - Полагают значение параметра
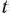 равным некоторому числу, принадлежащему оставшейся части промежутка
равным некоторому числу, принадлежащему оставшейся части промежутка 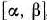 , и симплексным методом находят решение полученной задачи линейного программирования.
, и симплексным методом находят решение полученной задачи линейного программирования. - Определяют множество значений параметра
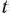 , для которых новый оптимальный план остается оптимальным или задача неразрешима. Вычисления повторяют до тех пор, пока не будут исследованы все значения параметра
, для которых новый оптимальный план остается оптимальным или задача неразрешима. Вычисления повторяют до тех пор, пока не будут исследованы все значения параметра 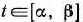 .
.
Примеры задач с решением:
- Задача 2.64. Для всех значений параметра найти максимальное значение функции
- Задача 2.65. Предприятие для изготовления различных изделий и использует три вида сырья. Нормы расхода сырья каждого вида на производство единицы продукции данного вида приведены в табл. 2.38. В ней же указана цена изделия каждого вида.
- Задача 2.67. Для производства продукции трех видов и необходимы три различных вида сырья. Каждый из видов сырья может быть использован в объеме, соответственно не большем чем 180, 210 и 244 кг. Нормы затрат каждого из видов сырья на единицу продукции данного вида и цена единицы продукции данного вида приведены в табл. 2.44.
Задачи дробно-линейного программирования
Экономическая и геометрическая интерпретации задачи дробно-линейного программирования. Общая задача дробно-линейного программирования состоит в определении максимального значения функции
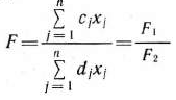
при условиях
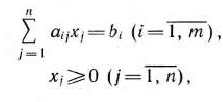
где
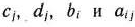
некоторые постоянные числа,
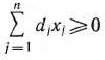
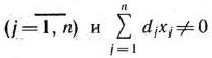
в области неотрицательных решений системы линейных уравнений (90). При этом будем предполагать, что
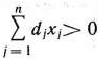
(такое условие не нарушает общности задачи, поскольку в том случае, когда эта величина отрицательна, знак минус можно отнести к числителю).
Как и в случае основной задачи линейного программирования, свое максимальное значение целевая функция задачи (89) — (91) принимает в одной йз вершин многогранника решений, определяемой системой ограничений (90) и (91) (естественно, при условии, что эта задача имеет оптимальный план). Если максимальное значение целевая функция задачи (89) принимает более чем в одной вершине многогранника решений, то она достигает его также во всякой точке, являющейся выпуклой комбинацией данных вершин.
Рассмотрим задачу, состоящую в определении максимального значения функции
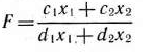
при условиях
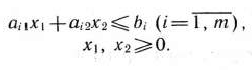
Будем считать, что
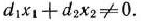
Чтобы найти решение задачи (92) — (94), как и в § 1.3 при рассмотрении задачи (19)— (21), сначала находим многоугольник решений, определяемый ограничениями (93) и (94). Предполагая, что этот многоугольник не пуст, полагаем значение функции равным некоторому числу h, так что прямая
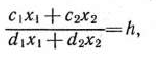
проходящая через начало координат, имеет общие точки с многоугольником решений. Вращая построенную прямую (95) вокруг начала координат, либо определяем вершину (вершины), в которой функция (92) принимает максимальное значение, либо устанавливаем неограниченность функции на множестве планов задачи.
Итак, процесс нахождения решения задачи (92) — (94) включает следующие этапы:
- В системе ограничений задачи заменяют знаки неравенств на знаки точных равенств и строят определяемые этими равенствами прямые.
- Находят полуплоскости, определяемые каждым из неравенств системы ограничений задачи.
- Находят многоугольник решений задачи.
- Строят прямую (95), уравнение которой получается, если положить значение целевой функции (92) равным некоторому постоянному числу.
- Определяют точку максимума или устанавливают неразрешимость задачи.
- Находят значение целевой функции в точке максимума.
Примеры задач с решением:
Задачи блочного программирования
В практике решения конкретных экономических задач встречаются задачи, системы ограничений которых включают ограничения, содержащие все переменные (эти ограничения образуют так называемую блок-связку), и ограничения, содержащие часть их (эти ограничения образуют блоки). Схематически система ограничений таких задач с двумя блоками изображена на рис. 2.13. В общем случае число блоков может быть значительным, а задачи, имеющие блочную структуру, могут быть задачами как линейного, так и нелинейного программирования.
Для решения задач линейного программирования с блочной структурой может быть использован так называемый метод декомпозиции Данцига—Вулфа*’, позволяющий свести решение конкретной задачи, содержащей несколько блоков, к решению отдельных подзадач, определяемых ими и соответствующим образом связанных между собой. При этом число блоков определяет количество подзадач, решаемых на каждой из итераций при решении так называемой главной задачи. Построим последнюю для задачи, содержащей два блока и состоящей в общем виде в определении максимального значения функции
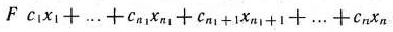
при условиях
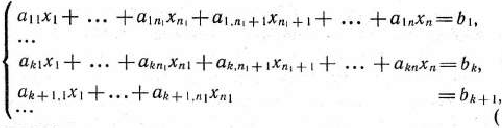
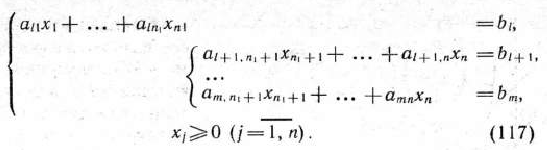
Прежде чем записать главную задачу, введем обозначения:

Обозначим через 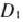 и
и 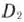 соответственно множества допустимых решений систем линейных уравнений:
соответственно множества допустимых решений систем линейных уравнений:

Пусть
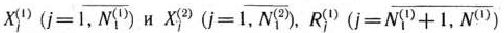
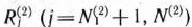
вершины и направляющие векторы неограниченных ребер соответственно многогранников 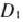 и
и 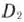 . Обозначим
. Обозначим
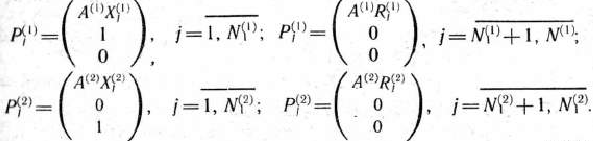
Далее,
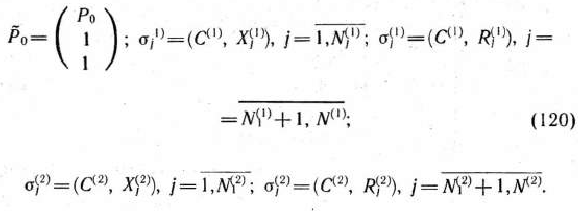
С учетом введенных обозначений главная задача состоит в определении максимального значения функции
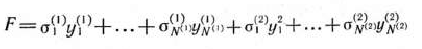
при условиях
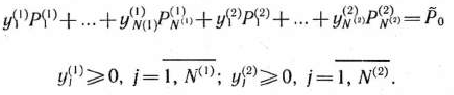
Если
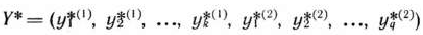
оптимальный план главной задачи,
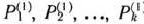
соответствующие вершины многогранника
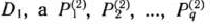
соответствующие направляющие векторы неограниченных ребер многогранника 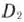 , то оптимальное решение исходной задачи есть
, то оптимальное решение исходной задачи есть
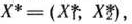
где
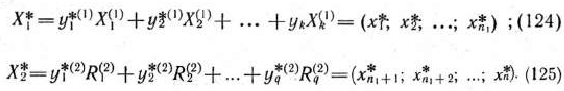
В том случае, когда целевая функция главной задачи не ограничена на допустимом множестве ее решений, это же относится и к целевой функции исходной задачи.
Примеры задач с решением:
- Задача 2.90. Построить главную задачу для задачи, состоящей в определении максимального значения функции
- Задача 2.98. Для производства двух видов изделий на двух предприятиях отрасли может быть использовано 480 ед. сырья. Нормы затрат сырья на одно изделие соответственно равны 4 н 3 ед., а прибыль от реализации одного изделия соответственно равна 5 и б руб.
Задачи теории игр и математическое программирование
Экономическая и геометрическая интерпретации задач теории игр. Если имеется несколько конфликтующих сторон (лиц), каждая из которых принимает некоторое решение, определяемое заданным набором правил, и каждому из лиц известно возможное конечное состояние конфликтной ситуации с заранее определенными для каждой из сторон платежами, то говорят, что имеет место игра. Задача теории игр состоит в выборе такой линии поведения данного игрока, отклонение от которой может лишь уменьшить его выигрыш.
Определение 2.5. Ситуация называется конфликтной, если в ней участвуют стороны, интересы которых полностью или частично противоположны.
Определен не 2.6. Игра — это действительный или формальный конфликт, в котором имеется по крайней мере два участника (игрока), каждый из которых стремится к достижению собственных целей.
Определение 2.7. Допустимые действия каждого из игроков, направленные на достижение некоторой цели, называются правилами игры.
Определение 2.8. Количественная оценка результатов игры называется платежом.
Определение 2.9. Игра называется парной, если в ней участвуют только две стороны (два лица).
Определение 2.10. Парная игра называется игрой с нулевой суммой, если сумма платежей равна нулю, т. е. если проигрыш одного игрока равен выигрышу второго.
Парные игры с нулевой суммой и рассматриваются ниже.
Определение 2.11. Однозначное описание выбора игрока в каждой из возможных ситуаций, при которой он должен сделать личный ход, называется стратегией игрока.
Определение 2.12. Стратегия игрока называется оптимальной, если при многократном повторении игры она обеспечивает игроку максимально возможный средний выигрыш (или, что то же самое, минимально возможный средний проигрыш).
Пусть имеется два игрока, один из которых может выбрать 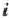 -ю стратегию из
-ю стратегию из 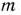 своих возможных стратегий
своих возможных стратегий 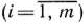 , а второй, не зная выбора первого, выбирает
, а второй, не зная выбора первого, выбирает 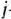 -ю стратегию из
-ю стратегию из 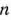 своих возможных стратегий
своих возможных стратегий 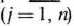 . В результате первый игрок выигрывает величину
. В результате первый игрок выигрывает величину 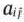 а второй проигрывает эту величину.
а второй проигрывает эту величину.
Из чисел 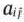 составим матрицу
составим матрицу
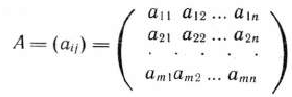
Строки матрицы А соответствуют стратегиям первого игрока, а столбцы —стратегиям второго. Эти стратегии называются чистыми.
Определение 2.13. Матрица А называется платежной (или матрицей игры).
Определение 2.14. Игру, определяемую матрицей А, имеющей  строк и
строк и  столбцов, называют конечной игрой размерности
столбцов, называют конечной игрой размерности  .
.
Определение 2.15. Число
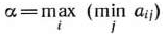
называется нижней ценой игры или максимином, а соответствующая ему стратегия (строка) —максиминной.
Определение 2.16. Число
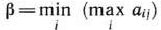
называется верхней ценой игры или минимаксом, а соответствующая ему стратегия игрока (столбец) —минимаксной.
Теорема 2.3. Нижняя цена игры всегда не превосходит верхней цены игры.
Определение 2.17. Если 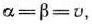 то число
то число 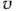 называется ценой игры.
называется ценой игры.
Задача 2.99.
Найти решение игры, заданной матрицей и дать геометрическую интерпретацию этого решения.
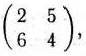
Решение. Прежде всего проверим наличие седловой точки в данной матрице. Для этого найдем минимальные элементы в каждой из строк (2 и 4) и максимальные элементы в каждом из столбцов (6 и 5). Значит, нижняя цена игры
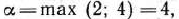
а верхняя цена игры
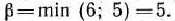
Так как
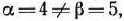
то решением игры являются смешанные оптимальные стратегии, а цена игры 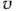 заключена в пределах
заключена в пределах
Предположим, что для игрока 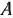 стратегия задается вектором
стратегия задается вектором 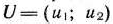 . Тогда на основании теоремы 2.6 при применении игроком
. Тогда на основании теоремы 2.6 при применении игроком 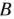 чистой стратегии
чистой стратегии 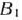 или
или 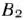 игрок
игрок 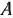 получит средний выигрыш, равный цене игры, т. е.
получит средний выигрыш, равный цене игры, т. е.
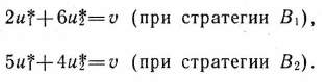
Помимо двух записанных уравнений относительно 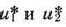 добавим уравнение, связывающее частоты
добавим уравнение, связывающее частоты 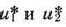 .
.
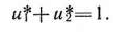
Решая полученную систему трех уравнений с тремя неизвестными, находим
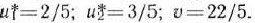
Найдем теперь оптимальную стратегию для игрока  . Пусть стратегия для данного игрока задается вектором
. Пусть стратегия для данного игрока задается вектором
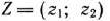
Тогда:
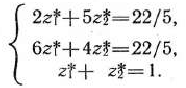
Решая систему уравнений, состоящую из каких-нибудь двух уравнений, взятых из последней системы, получим
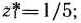
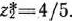
Следовательно, решением игры являются смешанные стратегии
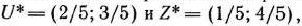
а цена игры
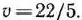
Дадим теперь геометрическую интерпретацию решения данной игры. Для этого на плоскости 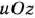 введем систему координат и на оси
введем систему координат и на оси  отложим отрезок единичной длины
отложим отрезок единичной длины 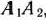 , каждой точке которого поставим в соответствие некоторую смешанную стратегию
, каждой точке которого поставим в соответствие некоторую смешанную стратегию
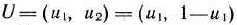
(рис. 2.15). В частности, точке 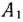 (0; 1) отвечает стратегия
(0; 1) отвечает стратегия 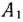 , точке
, точке  (1; 0) — стратегия
(1; 0) — стратегия 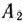 и т. д.
и т. д.
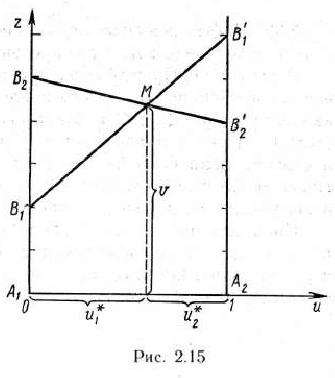
В точках 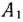 и
и 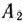 восставим лерпеидикуляры и на полученных прямых будем откладывать выигрыш игроков. На первом перпендикуляре (в данном случае он совпадает с осью
восставим лерпеидикуляры и на полученных прямых будем откладывать выигрыш игроков. На первом перпендикуляре (в данном случае он совпадает с осью 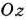 ) отложим выигрыш игрока
) отложим выигрыш игрока 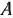 при стратегии
при стратегии 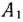 , а на втором — при стратегии
, а на втором — при стратегии 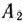 . Если игрок
. Если игрок 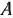 применяет стратегию
применяет стратегию 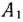 то его выигрыш при стратегии
то его выигрыш при стратегии 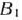 игрока
игрока 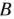 равен 2, а при стратегии
равен 2, а при стратегии 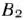 он равен 5. Числам 2 и 5 на оси
он равен 5. Числам 2 и 5 на оси 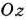 соответствуют точки
соответствуют точки 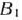 и
и 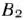 .
.
Если же игрок 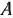 применяет стратегию
применяет стратегию 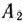 то его выигрыш при стратегии
то его выигрыш при стратегии 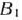 игрока
игрока 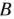 равен 6, а при стратегии
равен 6, а при стратегии 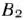 он равен 4. Эти два числа определяют две точки
он равен 4. Эти два числа определяют две точки 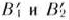 на перпендикуляре, восставленном в точке
на перпендикуляре, восставленном в точке 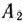 . Соединяя между собой точки
. Соединяя между собой точки 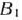 и
и 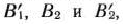 , получим две прямые, расстояние до которых от оси
, получим две прямые, расстояние до которых от оси  определяет средний выигрыш при любом сочетании соответствующих стратегий. Например, расстояние от любой точки отрезка
определяет средний выигрыш при любом сочетании соответствующих стратегий. Например, расстояние от любой точки отрезка 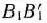 до оси
до оси  определяет средний выигрыш
определяет средний выигрыш 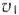 при любом сочетании стратегий
при любом сочетании стратегий 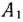 и
и 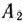 и стратегии игрока
и стратегии игрока 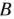 .
.
Таким образом, ординаты точек, принадлежащих ломаной 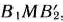 определяют минимальный выигрыш игрока
определяют минимальный выигрыш игрока 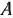 при применении им любых смешанных стратегий. Эта минимальная величина является максимальной в точке
при применении им любых смешанных стратегий. Эта минимальная величина является максимальной в точке 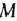 ; следовательно, этой точке соответствует оптимальная стратегия
; следовательно, этой точке соответствует оптимальная стратегия
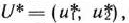
а ее ордината равна цене игры 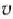 . Координаты точки
. Координаты точки 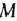 находим как координаты точки пересечения прямых
находим как координаты точки пересечения прямых 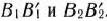 Соответствующие три уравнения имеют вид
Соответствующие три уравнения имеют вид
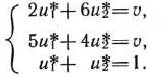
Решая последнюю систему уравнений, получаем
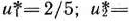
Аналогично находится оптимальная стратегия для игрока 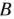 .
.
Для ее определения имеем уравнения
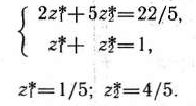
Следовательно, решением игры являются смешанные стратегии
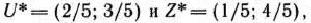
а цена игры
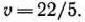
К такому выводу мы пришли и выше.
Обобщая изложенные выше результаты нахождения решения игры 2X2, можно указать основные этапы нахождения решения игры 2Х« или «X2.
- Строят прямые, соответствующие стратегиям второго (первого) игрока.
- Определяют нижнюю (верхнюю) границу выигрыша.
- Находят две стратегии второго (первого) игрока, которым соответствуют две прямые, псресекающисся в точке с максимальной (минимальной) ординатой.
- Определяют цену игры и оптимальные стратегии.
Примеры задач с решением:
- Задача 2.100. Найти решение игры, заданной матрицей
- Задача 2.101. Найти решение игры, заданной матрицей
- Задача 2.102. Швейное предприятие планирует к массовому выпуску новую модель одежды. Спрос на эту модель не может быть точно определен. Однако можно предположить, что его величина характеризуется тремя возможными состояниями (I, II, III). С учетом этих состояний анализируются три возможных варианта выпуска данной модели (А,Б, В).
- Задача 2.107. Построить игру, определяемую следующей парой двойственных задач.
Задачи нелинейного программирования. Экономическая и геометрическая интерпретации задачи нелинейного программирования
В общем виде задача нелинейного программирования состоит в определении максимального (минимального) значения функции
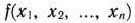
при условии, что ее переменные удовлетворяют соотношениям
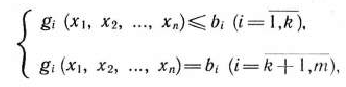
где  и
и  — некоторые известные функции
— некоторые известные функции 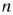 переменных, a
переменных, a 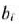 — заданные числа.
— заданные числа.
Здесь имеется в виду, что в результате решения задачи будет определена точка
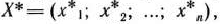
координаты которой удовлетворяют соотношениям (2) и такая, что для всякой другой точки
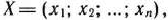
удовлетворяющей условиям (2), выполняется неравенство
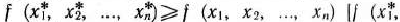
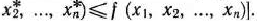
Если 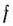 и
и 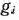 — линейные функции, то задача (1), (2) является задачей линейного программирования.
— линейные функции, то задача (1), (2) является задачей линейного программирования.
Соотношения (2) образуют систему ограничений и включают в себя условия неотрицательности переменных, если такие условия имеются. Условия неотрицательности переменных могут быть заданы и непосредственно.
В евклидовом пространстве 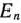 система ограничений (2) определяет область допустимых решений задачи. В отличие от задачи линейного программирования она не всегда является выпуклой.
система ограничений (2) определяет область допустимых решений задачи. В отличие от задачи линейного программирования она не всегда является выпуклой.
Если определена область допустимых решений, то нахождение решения задачи (1), (2) сводится к определению такой точки этой области, через которую проходит гиперповерхность наивысшего (наинизшего) уровня:

Указанная точка может находиться как на границе области допустимых решений, так и внутри нее.
Процесс нахождения решения задачи нелинейного программирования (1), (2) с использованием ее геометрической интерпретации включает следующие этапы:
- Находят область допустимых решений задачи, определяемую соотношениями (2) (если она пуста, то задача не имеет решения) .
- Строят гиперповерхность
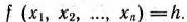
- Определяют гиперповерхность наивысшего (наинизшего) уровня или устанавливают неразрешимость задачи из-за неограниченности функции (1) сверху (снизу) на множестве допустимых решений.
- Находят точку области допустимых решений, через которую проходит гиперповерхность наивысшего (наинизшего) уровня, и определяют в ней значение функции (1).
Примеры задач с решением:
- Задача 3.1. Найти максимальное значение функции
- Задача 3.2. Найти максимальное и минимальное значения функции
- Задача 3.4. Найти максимальное значение функции
Метод множителей Лагранжа
Рассмотрим частный случай общей задачи нелинейного программирования (1), (2), предполагая, что система ограничений (2) содержит только уравнения, отсутствуют условия неотрицательности переменных и
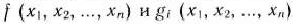
функции, непрерывные вместе со своими частными производными
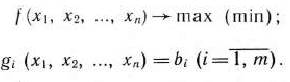
В курсе математического анализа задачу (16), (17) называют задачей на условный экстремум или классической задачей оптимизации.
Чтобы найти решение этой задачи, вводят набор переменных
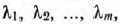
называемых множителями Лагранжа, составляют функцию Лагранжа
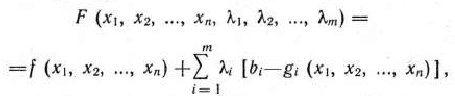
находят частные производные
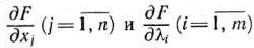
и рассматривают систему 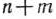 уравнений
уравнений
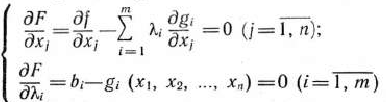
с 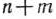 неизвестными
неизвестными
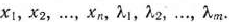
Всякое решение системы уравнений (19) определяет точку
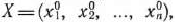
в которой может иметь место экстремум функции
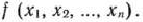
Следовательно, решив систему уравнений (19), получают все точки, в которых функция (16) может иметь экстремальные значения, Дальнейшее исследование найденных точек проводят так же, как и в случае безусловного экстремума.
Таким образом, определение экстремальных точек задачи (16), (17) методом множителей Лагранжа включает следующие этапы:
- Составляют функцию Лагранжа.
- Находят частные производные от функции Лагранжа по переменным
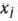 и
и 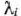 и приравнивают их нулю.
и приравнивают их нулю. - Решая систему уравнений (19), находят точки, в которых целевая функция задачи может иметь экстремум.
- Среди точек, подозрительных па экстремум, находят такие, в которых достигается экстремум, и вычисляют значения функции (16) в этих точках.
Примеры задач с решением:
- Задача 3.12. По плану производства продукции предприятию необходимо изготовить 180 изделий. Эти изделия могут быть изготовлены двумя технологическими способами. При производстве изделий I способом затраты равны руб., а при изготовлении изделий II способом они составляют руб. Определить, сколько изделий каждым из способов следует изготовить, так чтобы общие затраты на производство продукции были минимальными.
- Задача 3.13. Найти точки экстремума функции
Задачи выпуклого программирования
Рассмотрим задачу нелинейного программирования:
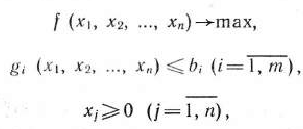
где 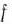 и
и 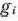 —некоторые функции
—некоторые функции 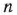 переменных
переменных 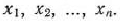 .
.
Для решения сформулированной задачи в такой общей постановке не существует универсальных методов. Однако для отдельных классов задач, в которых сделаны дополнительные ограничения относительно свойств функций 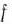 и
и 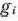 разработаны эффективные методы их решения. В частности, ряд таких методов имеется для решения задач нелинейного программирования (24) — (26) при условии, что
разработаны эффективные методы их решения. В частности, ряд таких методов имеется для решения задач нелинейного программирования (24) — (26) при условии, что 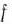 — вогнутая (выпуклая) функция и область допустимых решений, определяемая ограничениями (25) и (26),— выпуклая.
— вогнутая (выпуклая) функция и область допустимых решений, определяемая ограничениями (25) и (26),— выпуклая.
Определение 3.1. Функция
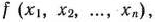
заданная на выпуклом множестве 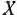 , называется выпуклой, если для любых двух точек
, называется выпуклой, если для любых двух точек 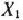 и
и 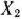 из
из 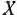 и любого
и любого 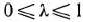 выполняется соотношение
выполняется соотношение
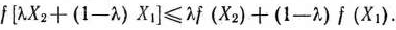
Определение 3.2. Функция
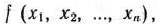
заданная на выпуклом множестве  , называется вогнутой, если для любых двух точек
, называется вогнутой, если для любых двух точек 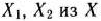 и любого
и любого 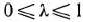 выполняется соотношение
выполняется соотношение
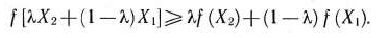
Определение 3.3. Говорят, что множество допустимых решений задачи (24) — (26) удовлетворяет условию регулярности, если существует по крайней мере одна точка 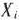 , принадлежащая области допустимых решений такая, что
, принадлежащая области допустимых решений такая, что
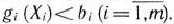
Определение 3.4. Задача (24) — (26) называется задачей выпуклого программирования, если функция
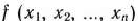
является вогнутой (выпуклой), а функции
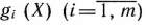
выпуклыми.
Теорема 3.1. Любой локальный максимijm (минимум) задачи выпуклого программирования является глобальным максимумом (минимумом).
Оп ределение 3.5. Функцией Лагранжа задачи выпуклого программирования (24)—(26) называется функция
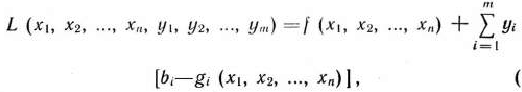
где
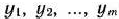
множители Лагранжа.
Определение 3.6. Точка
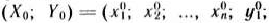
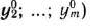
называется седловой точкой функции Лагранжа, если
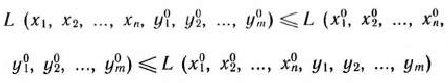
для всех
Теорема 3,2 (теорема Куна—Таккера). Для задачи выпуклого программирования (24) — (26), множество допустимых решений которой обладает свойством регулярности, 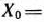
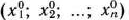 является оптимальным планом тогда и только тогда, когда существует такой вектор
является оптимальным планом тогда и только тогда, когда существует такой вектор 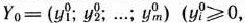
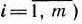 , что
, что 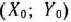 — седловая точка функции Лагранжа.
— седловая точка функции Лагранжа.
Если предположить, что целевая функция 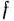 и функция
и функция 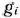 непрерывно дифференцируемы, то теорема Куна—Таккера может быть дополнена аналитическими выражениями, определяющими необходимые и достаточные условия того, чтобы точка
непрерывно дифференцируемы, то теорема Куна—Таккера может быть дополнена аналитическими выражениями, определяющими необходимые и достаточные условия того, чтобы точка 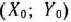 была седловой точкой функции Лагранжа, т. е. являлась решением задачи выпуклого программирования. Эти выражения имеют следующим вид
была седловой точкой функции Лагранжа, т. е. являлась решением задачи выпуклого программирования. Эти выражения имеют следующим вид
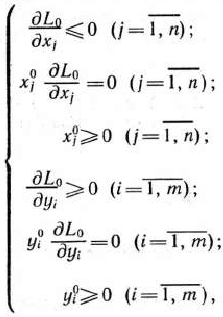
где 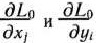 —значения соответствующих частных производных функции Лагранжа, вычисленных в седловой точке. Всем отмеченным выше требованиям, позволяющим записать необходимые и достаточные условия для седловой точки
—значения соответствующих частных производных функции Лагранжа, вычисленных в седловой точке. Всем отмеченным выше требованиям, позволяющим записать необходимые и достаточные условия для седловой точки 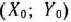 функции Лагранжа в виде выражений (30) — (35), удовлетворяет сформулированная ниже задача квадратичного программирования. Прежде чем сформулировать эту задачу, дадим некоторые определения.
функции Лагранжа в виде выражений (30) — (35), удовлетворяет сформулированная ниже задача квадратичного программирования. Прежде чем сформулировать эту задачу, дадим некоторые определения.
Определение 3.7. Квадратичной формой относительно переменных
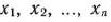
называется числовая функция от этих переменных, имеющая вид
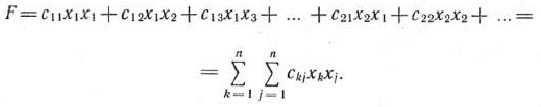
Определение 3.8. Квадратичная форма 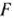 называется положительно (отрицательно)-определенной, если
называется положительно (отрицательно)-определенной, если 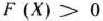
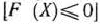 для всех значений переменных
для всех значений переменных 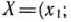
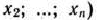 , кроме
, кроме 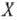 = 0.
= 0.
Определение 3.9. Квадратичная форма 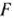 называется положительно(отрицательно)-полуопределенной, если
называется положительно(отрицательно)-полуопределенной, если
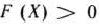
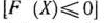
для любого набора значений переменных
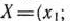
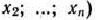
и, кроме того, существует такой набор переменных
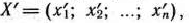
где не все значения переменных одновременно равны нулю, что
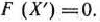
Теорема 3.3. Квадратичная форма является выпуклой функцией, если она положительно-полуопределенная, и вогнутой функцией, если она отрицательно-полуопределенная.
Определение 3.10. Задача, состоящая в определении максимального (минимального) значения функции
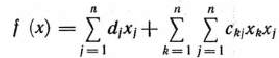
при ограничениях
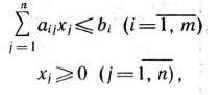
где
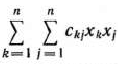
отрицательно(положительно) полуопределенная квадратичная форма, называется задачей квадратичного программирования.
Для сформулироааннои задачи квадратичного программирования функция Лагранжа запишется и виде

Если функция 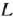 имеет седловую точку
имеет седловую точку
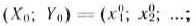
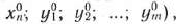
то в этой точке наполняются соотношения (30) — (35). Вводя теперь дополнительные церемонные
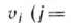
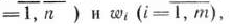
обращающие неравенства (30) и (33) в равенства, перепишем выражении (30) — (35), записанные для задачи квадратичного программирования, следующим образом:
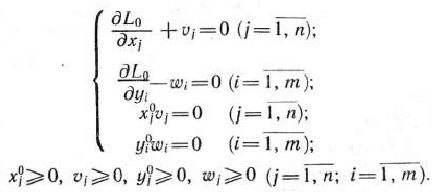
Таким образом, чтобы найти решение задачи квадратичного программирования (36) — (38), нужно определить неотрицательное решение систем линейных уравнений (39) и (40), удовлетворяющее условиям (41) и (42). Это решение можно найти с помощью метода искусственного базиса, примененного для нахождения максимального значения функции 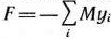 . При условиях (39), (40), (43) с учетом (41) и (42). Здесь
. При условиях (39), (40), (43) с учетом (41) и (42). Здесь 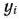 — искусственные переменные, введенные в уравнения (39) и (40).
— искусственные переменные, введенные в уравнения (39) и (40).
Используя метод искусственного базиса и дополнительно учитывая условия (41) и (42), после конечного числа шагов либо установим неразрешимость, либо получим оптимальный план исходной задачи.
Итак, процесс нахождения решения задачи квадратичного программирования (36) — (38) включает следующие этапы:
- Составляют функцию Лагранжа.
- Записывают в виде выражений (39) — (43) необходимые и достаточные условия существования седловой точки для функции Лагранжа.
- Используя метод искусственного базиса, либо устанавливают отсутствие седловой точки для функции Лагранжа, либо находят ее координаты.
- Записывают оптимальное решение исходной задачи и находят значение целевой функции.
Пример задачи с решением:
Градиентные методы
Используя градиентные методы, можно найти решение любой задачи нелинейного программирования. Однако в общем случае применение этих методов позволяет найти точку локального экстремума. Поэтому более целесообразно использовать градиентные методы для нахождения решения задач выпуклого программирования, в которых всякий локальный экстремум является одновременно и глобальным. Процесс нахождения решения задачи с помощью градиентных методов состоит в том, что начиная с некоторой точки Xосуществляется последовательный переход к некоторым другим точкам до тех пор, пока не выявляется приемлемое решение исходной задачи. При этом градиентные методы могут быть подразделены на две группы.
К первой группе относятся методы, при использовании которых исследуемые точки не выходят за пределы области допустимых решений задачи. Наиболее распространенным из таких методов является метод Франка—Вулфа.
Ко второй группе относятся методы, при использовании которых исследуемые точки могут как принадлежать, так и не принадлежать области допустимых решений. Однако в результате реализации итерационного процесса находится точка области допустимых решений, определяющая приемлемое решение. Из таких методов наиболее часто используется метод штрафных функций или метод Эрроу—Гурвица.
При нахождении решения задач градиентными методами, в том числе и названными, итерационный процесс осуществляется до того момента, пока градиент функции
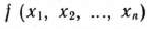
в очередной точке 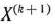 не станет равным нулю или же пока
не станет равным нулю или же пока
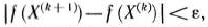
где 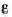 — достаточно малое положительное число, характеризующее точность полученного решения.
— достаточно малое положительное число, характеризующее точность полученного решения.
Остановимся более подробно на методах Франка—Вулфа, штрафных функций и Эрроу Гурвица.
I. Метод Франка—Вулфа. Пусть требуется найти максимальное значение вогнутой функции
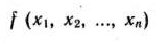
при условиях
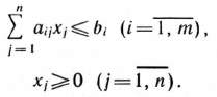
Характерной особенностью этой задачи является то, что ее система ограничений содержит только линейные неравенства. Эта особенность является основой для замены в окрестности исследуемой точки нелинейной целевой функции линейной, благодаря чему решение исходной задачи сводится к последовательному решению задач линейного программирования.
Процесс нахождения решения задачи начинают с определения точки, принадлежащей области допустимых решений задачи. Пусть это точка 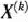 тогда в этой точке вычисляют градиент функции (57)
тогда в этой точке вычисляют градиент функции (57)
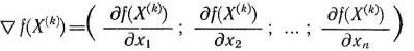
и строят линейную функцию
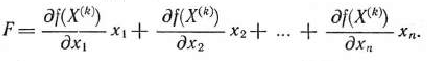
Затем находят максимальное знамение этой функции при ограничениях (58) и (59). Пусть решение данной задачи определяется точкой 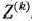 . Тогда за новое допустимое решение исходной задачи принимают координаты точки
. Тогда за новое допустимое решение исходной задачи принимают координаты точки 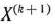 :
:
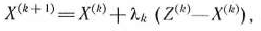
где 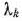 — некоторое число, называемое шагом вычислении и заключенное между нулем и единицей
— некоторое число, называемое шагом вычислении и заключенное между нулем и единицей 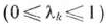 . Это число
. Это число 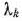 берут произвольно или определяют таким образом, чтобы значение функции в точке
берут произвольно или определяют таким образом, чтобы значение функции в точке 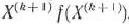 . зависящее от
. зависящее от 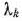 было максимальным. Для этого необходимо найти решение уравнения
было максимальным. Для этого необходимо найти решение уравнения 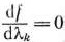 и выбрать его наименьший корень. Если его значение больше единицы, то следует положить
и выбрать его наименьший корень. Если его значение больше единицы, то следует положить 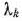 = 1. После определения числа
= 1. После определения числа 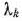 находят координаты точки вычисляют значение целевой функции в ней и выясняют необходимость перехода к попой точке
находят координаты точки вычисляют значение целевой функции в ней и выясняют необходимость перехода к попой точке 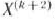 . Если такая необходимость имеется, то вычисляют в точке градиент целевой функции, переходят к соответствующей задаче линейного программирования и находят се решение. Определяют координаты точки и исследуют необходимость проведения дальнейших вычислений. После конечного числа шагов получают с необходимой точностью решение исходной задачи.
. Если такая необходимость имеется, то вычисляют в точке градиент целевой функции, переходят к соответствующей задаче линейного программирования и находят се решение. Определяют координаты точки и исследуют необходимость проведения дальнейших вычислений. После конечного числа шагов получают с необходимой точностью решение исходной задачи.
Итак, процесс нахождения решения задачи (57) — (50) методом Франка—Вулфа включает следующие этапы:
- Определяют исходное допустимое решение задачи.
- Находят градиент функции (57) в точке допустимого решения.
- Строят функцию (60) н находят ее максимальное значение при условиях (58) и (59).
- Определяют шаг вычислений.
- По формулам (61) находят компоненты нового допустимого решения.
- Проверяют необходимость перехода к последующему допустимому решению. В случае необходимости переходят к этапу 2, в противном случае найдено приемлемое решение исходной задачи.
Пример задачи с решением:
Нахождение решения задач нелинейного программирования, содержащих сепарабельные функции
Рассмотрим задачу нелинейного программирования, в которой целевая функция и функции в системе ограничений являются сепарабельными.
Определение 3.11. Функция
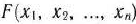
называется сепарабельной, если она может быть представлена в виде суммы функций, каждая из которых является функцией одной переменной, т. е. если
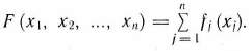
Если целевая функция и функции в системе ограничений задачи нелинейного программирования являются сепарабельными, то приближенное решение такой задачи можно найти с использованием метода кусочно-линейной аппроксимации. Однако его применение в общем случае позволяет получить приближенный локальный экстремум. Поэтому рассмотрим использование метода кусочно-линейной аппроксимации для решения задачи выпуклого программирования.
I. Метод кусочно-линейной аппроксимации. Пусть требуется определить максимальное значение вогнутой функции
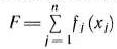
при условиях
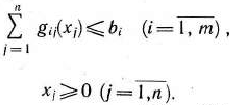
Чтобы найти решение задачи (80) —(82), заменим функции
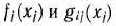
кусочно-линейными функциями
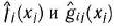
и перейдем от задачи (80) — (82) к задаче, состоящей в определении максимального значения функции
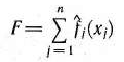
при условиях
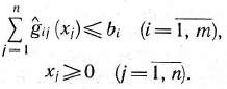
В задаче (83) —(85) пока не определен вид функций. Чтобы сделать это, будем считать, что переменная 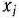 может принимать значения из промежутка
может принимать значения из промежутка 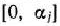 (
(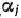 — максимальное значение переменной
— максимальное значение переменной 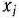 ). Разобьем промежуток
). Разобьем промежуток 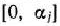 на
на 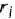 промежутков с помощью
промежутков с помощью 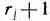 точек так, что
точек так, что 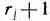 . Тогда функции
. Тогда функции
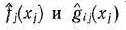
можно записать в виде
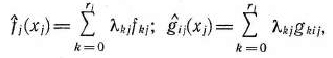
где
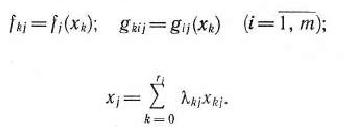
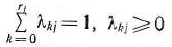
не более двух чисел 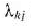 могут быть положительными и должны быть соседними.
могут быть положительными и должны быть соседними.
Подставляя теперь в равенства (83) и (84) выражения функций

в соответствии с формулами (86), приходим к следующей задаче:
Найти максимальное значение функции
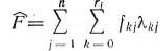
при условиях
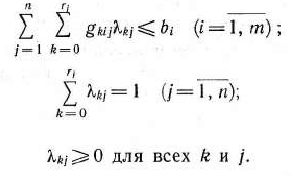
Полученная задача отличается от обычной задачи линейного программирования тем, что наложено дополнительное ограничение на переменную состоящее в том, чтобы для каждого 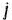 не более двух
не более двух 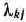 были положительными и эти положительные
были положительными и эти положительные 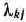 , были соседними.
, были соседними.
Выполнение этих условий может быть соблюдено при решении задачи (88) — (91) симплексным методом за счет соответствующего выбора базиса, определяющего как каждый опорный, так и оптимальный план данной задачи.
При этом в общем случае точность полученного решения зависит от принятого шага разбиения промежутка 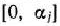 . Чем меньше шаг, тем более точным является полученное решение.
. Чем меньше шаг, тем более точным является полученное решение.
Таким образом, процесс нахождения решения задачи нелинейного программирования методом кусочно-линейной аппроксимации включает следующие этапы:
- Каждую из сепарабельных функций заменяют кусочно-линейной функцией.
- Строят задачу линейного программирования (88)—(91).
- С помощью симплексного метода находят решение задачи (88) —(91).
- Определяют оптимальный план задачи (80) — (82) и находят значение целевой функции при этом плане.
Пример задачи с решением:
Использование ППП ЛП АСУ для решения задачи нелинейного программирования
Используя ППП ЛП АСУ, можно решить любую задачу нелинейного программирования, целевая функция и система ограничений которой содержат сепарабель-ные функции. Для ее решения применяется дельта-метод кусочно-линейной аппроксимации. Его применение позволяет находить приближенное решение задач нелинейного программирования при К) ООО ограничений (при любом числе переменных) на машинах с оперативной памятью 1024 Кбайт.
Процесс нахождения решения задачи нелинейного программирования с использованием 111111 ЛП АСУ включает те же основные этапы, что и процесс нахождения решения задачи линейного программирования с применением данного пакета. Вместе с тем имеются определенные различия как в записи исходных данных задачи на бланке, так и в управляющей программе решения задачи, которая содержит еще один оператор XSETLB.
Основная особенность записи исходных данных задачи нелинейного программирования состоит в том, что по каждому набору вспомогательных переменных вводятся маркеры начала и конца набора переменных.
Каждый набор переменных имеет свое имя. Это имя записывается в поле 2, в поле 3 помещается ключевое слово ‘MARKER’, а в поле 5— ключевое слово начала набора ‘SEPORG’. Если при этом наборы вспомогательных переменных идут один за другим, то имя конца набора может быть одним и тем же.
Заметим, что, прежде чем приступить к записи исходных данных данной задачи, нужно определенным образом подготовить их к этому на бланке. Такая подготовка связана с заменой сепарабельных функций задачи на кусочно-линейные, о чем подробно сказано выше.
Пример задачи с решением:
Задачи динамического программирования. Общая характеристика задач динамического программирования и их геометрическая и экономическая интерпретации
В рассмотренных выше задачах линейного и нелинейного программирования мы находили их решение как бы в один этап или за один шаг. Такие задачи получили название одноэтапных или одношаговых.
В отличие от этих задач задачи динамического программирования являются многоэтапными или многошаговыми. Иешми словами, нахождение решения конкретных задач методами динамического программирования включает несколько этапов или шагов, на каждом из которых определяется решение некоторой частной задачи, обусловленной исходной. Поэтому термин «динамическое программирование» не столько определяет особый тип задач, сколько характеризует методы нахождения решения отдельных классов задач математического программирования, которые могут относиться к задачам как линейного, так и нелинейного программирования. Несмотря на это, целесообразно дать общую постановку задачи динамического программирования и определить единый подход к ее решению.
Предположим, что данная физическая система 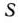 находится в некотором начальном состоянии
находится в некотором начальном состоянии 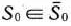 и является управляемой. Таким образом, благодаря осуществлению некоторого управления
и является управляемой. Таким образом, благодаря осуществлению некоторого управления 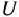 указанная система переходит из начального состояния
указанная система переходит из начального состояния 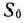 в конечное состояние
в конечное состояние 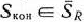 . При этом качество каждого из реализуемых управлений
. При этом качество каждого из реализуемых управлений 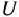 характеризуется соответствующим значением функции
характеризуется соответствующим значением функции 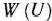 . Задача состоит в том, чтобы из множества возможных управлений
. Задача состоит в том, чтобы из множества возможных управлений 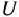 найти такое
найти такое 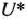 , при котором функция
, при котором функция 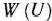 принимает экстремальное (максимальное или минимальное) значение
принимает экстремальное (максимальное или минимальное) значение 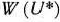 . Сформулированная задача и является общей задачей динамического программирования.
. Сформулированная задача и является общей задачей динамического программирования.
Дадим геометрическую интерпретацию этой задачи. Предположим, что состояние системы характеризуется некоторой точкой 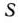 на плоскости
на плоскости 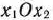 (рис. 4.1) и эта точка благодаря осуществляемому управлению ее движением перемещается вдоль линии.
(рис. 4.1) и эта точка благодаря осуществляемому управлению ее движением перемещается вдоль линии.
изображенной на рис. 4.1, из области возможных начальных состояний 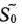 в область допустимых конечных состояний
в область допустимых конечных состояний 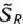 . Каждому управлению
. Каждому управлению 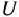 движением точки, т. е. каждой траектории движения точки, поставим в соответствие значение некоторой функции
движением точки, т. е. каждой траектории движения точки, поставим в соответствие значение некоторой функции 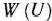 (например, длину пути, пройденного точкой под воздействием данного управления). Тогда задача состоит в том, чтобы из всех допустимых траекторий движения точки
(например, длину пути, пройденного точкой под воздействием данного управления). Тогда задача состоит в том, чтобы из всех допустимых траекторий движения точки 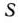 найти такую, которая получается в результате реализации управления
найти такую, которая получается в результате реализации управления 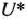 , обеспечивающего экстремальное значение функции
, обеспечивающего экстремальное значение функции 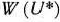 . К определению такой «траектории» сводится и задача динамического программирования в случае, когда допустимые состояния системы
. К определению такой «траектории» сводится и задача динамического программирования в случае, когда допустимые состояния системы 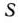 определяются точками
определяются точками 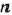 -мерного пространства.
-мерного пространства.
Экономическую интерпретацию общей задачи динамического программирования рассмотрим на конкретных примерах.
Пример задачи с решением:
Нахождение решения задач методом динамического программирования
В предыдущем параграфе была дана постановка общей задачи динамического программирования и приведены ее геометрическая и экономическая интерпретации. Рассмотрим теперь в общем виде решение этой задачи. Для этого введем некоторые обозначения и сделаем необходимые для дальнейших изложений предположения.
Будем считать, что состояние рассматриваемой системы 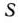 на
на 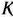 -м шаге
-м шаге 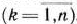 определяется совокупностью чисел
определяется совокупностью чисел
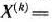
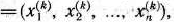
которые получены в результате реализации управления 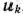 , обеспечившего переход системы
, обеспечившего переход системы 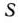 из состояния
из состояния 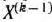 в состояние
в состояние 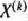 При этом будем предполагать, что состояние
При этом будем предполагать, что состояние 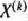 , в которое перешла система
, в которое перешла система 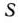 , зависит от данного состояния и выбранного управления
, зависит от данного состояния и выбранного управления 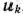 и не зависит от того, каким образом система
и не зависит от того, каким образом система 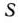 пришла в состояние
пришла в состояние 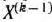 .
.
Далее, будем считать, что если в результате реализации 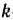 -го шага обеспечен определенный доход или выигрыш, также зависящий от исходного состояния системы
-го шага обеспечен определенный доход или выигрыш, также зависящий от исходного состояния системы 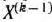 и выбранного управления
и выбранного управления 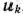 и равный
и равный 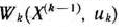 , то общий доход или выигрыш за
, то общий доход или выигрыш за 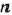 шагов составляет
шагов составляет
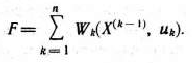
Таким образом, мы сформулировали два условия, которым должна удовлетворять рассматриваемая задача динамического программирования. Первое условие обычно называют условием отсутствия последействия, а второе — условием аддитивности целевой функции задачи.
Выполнение для задачи динамического программирования первого условия позволяет сформулировать для нес принцип оптимальности Беллмана. Прежде чем сделать это, дадим определение оптимальной стратегии управления. Под такой стратегией будем понимать совокупность управлений
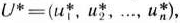
в результате реализации которых система 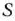 за
за 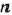 шагов переходит из начального состояния .
шагов переходит из начального состояния .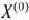 в конечное
в конечное 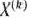 и при этом функция (4) принимает наибольшее значение.
и при этом функция (4) принимает наибольшее значение.
Принцип оптимальности. Каково бы ни било состояние системы перед очередным шагом, надо выбрать управление на этом шаге так, чтобы выигрыш на данном шаге плюс оптимальный выигрыш на всех последующих шагах был максимальным.
Отсюда следует, что оптимальную стратегию управления можно получить, если сначала найти оптимальную стратегию управления на 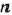 -м шаге, затем на двух последних шагах, затем на трех последних шагах и т. д., вплоть до первого шага. Таким образом, решение рассматриваемой задачи динамического программирования целесообразно начинать с определения оптимального решения на последнем,
-м шаге, затем на двух последних шагах, затем на трех последних шагах и т. д., вплоть до первого шага. Таким образом, решение рассматриваемой задачи динамического программирования целесообразно начинать с определения оптимального решения на последнем, 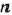 -м шаге. Для того чтобы найти то решение, очевидно, нужно сделать различные предположения о том, как мог окончиться предпоследний шаг, и с учетом этого выбрать управление
-м шаге. Для того чтобы найти то решение, очевидно, нужно сделать различные предположения о том, как мог окончиться предпоследний шаг, и с учетом этого выбрать управление 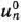 , обеспечивающее максимальное значение функции
, обеспечивающее максимальное значение функции
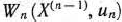
Такое управление 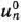 , выбранное при определенных предположениях о том, как окончился предыдущий шаг, называется условно оптимальным управлением. Следовательно, принцип оптимальности требует находить на каждом шаге условно оптимальное управление для любого из возможных исходов предшествующего шага.
, выбранное при определенных предположениях о том, как окончился предыдущий шаг, называется условно оптимальным управлением. Следовательно, принцип оптимальности требует находить на каждом шаге условно оптимальное управление для любого из возможных исходов предшествующего шага.
Чтобы это можно было осуществить практически, необходимо дать математическую формулировку принципа оптимальности. Для этого введем некоторые дополнительные обозначения. Обозначим через 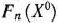 максимальный доход, получаемый за
максимальный доход, получаемый за 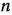 шагов при переходе системы
шагов при переходе системы 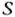 из начального состояния
из начального состояния 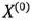 в конечное состояние
в конечное состояние 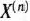 при реализации оптимальной стратегии управления
при реализации оптимальной стратегии управления
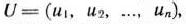
а через 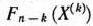 — максимальный доход, получаемый при переходе из любого состояния
— максимальный доход, получаемый при переходе из любого состояния 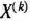 в конечное состояние
в конечное состояние 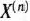 при оптимальной стратегии управления на оставшихся
при оптимальной стратегии управления на оставшихся  шагах. Тогда
шагах. Тогда
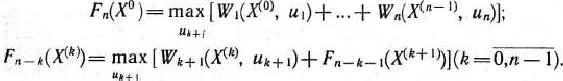
Последнее выражение представляет собой математическую запись принципа оптимальности и носит название основного функционального уравнения Беллмана или рекуррентного соотношения. Используя данное уравнение, находим решение рассматриваемой задачи динамического программирования. Остановимся на этом более подробно.
Полагая 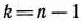 в рекуррентном соотношении (6), получаем следующее функциональное уравнение;
в рекуррентном соотношении (6), получаем следующее функциональное уравнение;
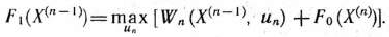
В этом уравнении 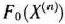 будем считать известным. Используя теперь уравнение (7) и рассматривая всевозможные допустимые состояния системы
будем считать известным. Используя теперь уравнение (7) и рассматривая всевозможные допустимые состояния системы  на
на  -м шаге
-м шаге
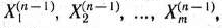
…, находим условные оптимальные решения
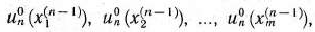
и соответствующие значения функции (7)
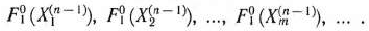
Таким образом, на 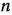 -м шаге находим условно оптимальное управление при любом допустимом состоянии системы
-м шаге находим условно оптимальное управление при любом допустимом состоянии системы 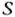 после
после  -го шага. Иными словами, в каком бы состоянии система ни оказалась после
-го шага. Иными словами, в каком бы состоянии система ни оказалась после  -го шага, нам уже известно, какое следует принять решение на
-го шага, нам уже известно, какое следует принять решение на 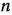 -м шаге. Известно также и соответствующее значение функции (7).
-м шаге. Известно также и соответствующее значение функции (7).
Переходим теперь к рассмотрению функционального уравнения при 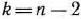 :
:
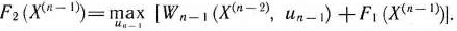
Для того чтобы найти значения 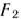 для всех допустимых значений
для всех допустимых значений 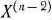 , очевидно, необходимо знать
, очевидно, необходимо знать 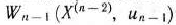 и
и 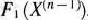 . Что касается значений
. Что касается значений 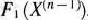 , то мы их уже определили. Поэтому нужно произвести вычисления для
, то мы их уже определили. Поэтому нужно произвести вычисления для 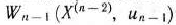 при некотором наборе допустимых значений
при некотором наборе допустимых значений 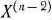 и соответствующих управлений
и соответствующих управлений 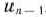 . Эти вычисления позволят определить условно оптимальное управление
. Эти вычисления позволят определить условно оптимальное управление 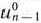 для каждого
для каждого 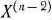 . Каждое из таких управлений совместно с уже выбранным управлением на последнем шаге обеспечивает максимальное значение дохода на двух последних шагах.
. Каждое из таких управлений совместно с уже выбранным управлением на последнем шаге обеспечивает максимальное значение дохода на двух последних шагах.
Последовательно осуществляя описанный выше итерационный процесс, дойдем, наконец, до первого шага. На этом шаге нам известно, в каком состоянии может находиться система. поэтому уже не требуется делать предположений о допустимых состояниях системы, а остается лишь только выбрать управление, которое является наилучшим с учетом условно оптимальных управлений, уже принятых на всех последующих шагах.
Таким образом, в результате последовательного прохождения всех этапов от конца к началу определяем максимальное значение выигрыша за п шагов и для каждого из них находим условно оптимальное управление.
Чтобы найти оптимальную стратегию управления, т. е. определить искомое решение задачи, нужно теперь пройти всю последовательность шагов, только на этот раз от начала к концу. А именно: на первом шаге в качестве оптимального управления 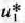 возьмем найденное условно оптимальное управление
возьмем найденное условно оптимальное управление 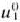 . На втором шаге найдем состояние
. На втором шаге найдем состояние 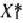 , в которое переводит систему управление
, в которое переводит систему управление 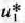 . Это состояние определяет найденное условно оптимальное управление которое теперь будем считать оптимальным. Зная
. Это состояние определяет найденное условно оптимальное управление которое теперь будем считать оптимальным. Зная  , находим
, находим 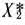 , а значит, определяем и т. д. В результате этого находим решение задачи, т. е. максимально возможный доход и оптимальную стратегию управления
, а значит, определяем и т. д. В результате этого находим решение задачи, т. е. максимально возможный доход и оптимальную стратегию управления 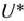 , включающую оптимальные управления на отдельных шагах;
, включающую оптимальные управления на отдельных шагах;
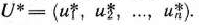
Итак, мы рассмотрели в общем виде нахождение решения задачи динамического программирования. Из изложенного видно, что этот процесс является довольно громоздким. Поэтому ниже рассмотрено нахождение решения самых простых задач, допускающих постановку в терминах общей задачи динамического программирования. Вместе с тем отметим, что использование ЭВМ позволяет находить на основе описанного выше подхода решение и более сложных практических задач.
Кстати готовые на продажу задачи тут, и там же теория из учебников может быть вам поможет она.
Примеры задач с решением:
- Задача 4.9. К началу текущей пятилетки на предприятии установлено новое оборудование. Зависимость производительности этого оборудования от времени его использования предприятием, а также зависимость затрат на содержание и ремонт оборудования при различном времени его использования
- Задача 4.10. Найти решение задачи 4.2, если тыс. руб., , а значения и приведены в табл. 4.7.
Возможно эти страницы вам будут полезны:
- Решение задач по математическому программированию
- Заказать работу по математическому программированию
- Помощь по математическому программированию
- Задачи математического программирования
- Задача линейного программирования
- Решение задач по линейному программированию
- Методы решения задач линейного программирования
- Графическое решение задач линейного программирования
- Графический метод решения задач линейного программирования
- Заказать работу по линейному программированию
- Помощь по линейному программированию
- Контрольная работа по линейному программированию
- Линейное программирование в Excel
- Курсовая работа по линейному программированию
