Задача 2.59.
Предприятие должно выпустить два вида продукции 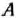 и
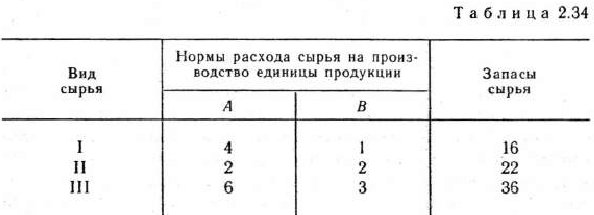
и 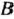 , для изготовления которых используется три вида сырья. Нормы расхода сырья каждого вида на производство единицы продукции данного вида приведены в табл. 2.34. В ней же указаны запасы сырья каждого вида, которое может быть использовано на производство единицы продукции данного вида.
, для изготовления которых используется три вида сырья. Нормы расхода сырья каждого вида на производство единицы продукции данного вида приведены в табл. 2.34. В ней же указаны запасы сырья каждого вида, которое может быть использовано на производство единицы продукции данного вида.
Известно, что цена единицы продукции может изменяться для изделия 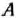 от 2 до 12 руб., а для изделия
от 2 до 12 руб., а для изделия 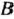 — от 13 до 3 руб., причем эти изменения определяются соотношениями
— от 13 до 3 руб., причем эти изменения определяются соотношениями 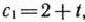
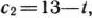 где
где 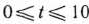 .
.
Для каждого из возможных значений цены единицы продукции каждого из видов найти такой план их производства, при котором общая стоимость продукции является максимальной.
Решение:
Предположим, что предприятие изготовит 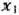 единиц продукции
единиц продукции 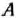 и
и 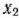 единиц продукции
единиц продукции 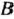 . Тогда математическая постановка задачи состоит в определении для каждого значения параметра
. Тогда математическая постановка задачи состоит в определении для каждого значения параметра 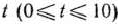 максимального значения
максимального значения
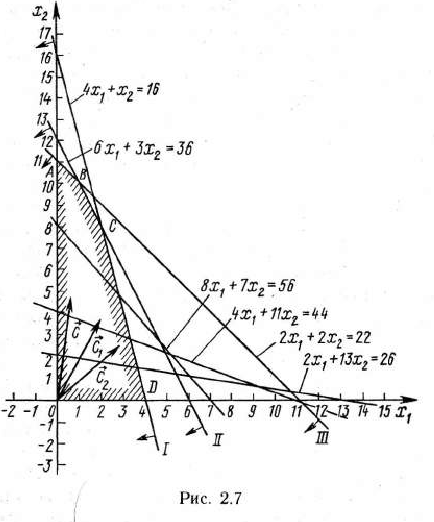
функции
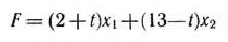
при условиях
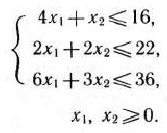
Чтобы найти решение задачи (69) — (71), строим многоугольник решений, определяемый системой линейных неравенств (70) и условием неотрицательности переменных (71) (рис. 2.7). После этого, полагая 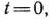 , строим прямую
, строим прямую 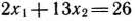 (число 26 взято произвольно) и вектор
(число 26 взято произвольно) и вектор 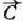 = (2; 13). Передвигая построенную прямую в направлении вектора
= (2; 13). Передвигая построенную прямую в направлении вектора 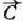 , видим, что последней общей точкой ее с многоугольником решений
, видим, что последней общей точкой ее с многоугольником решений 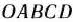 является точка
является точка 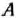 (0; 11). Следовательно, задача, полученная из задачи (69) —(71) при
(0; 11). Следовательно, задача, полученная из задачи (69) —(71) при 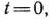 имеет оптимальный план
имеет оптимальный план 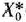 =(0;11). Это означает, что если цена единицы продукции
=(0;11). Это означает, что если цена единицы продукции 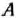 равна 2 + 0 = 2 руб., а цена единицы продукции
равна 2 + 0 = 2 руб., а цена единицы продукции 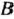 равна 13—0= 13 руб., то оптимальным планом производства является план, согласно которому производится II изделий
равна 13—0= 13 руб., то оптимальным планом производства является план, согласно которому производится II изделий 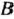 и не производятся изделия
и не производятся изделия 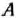 . При таком плане производства продукции ее стоимость максимальна и равна
. При таком плане производства продукции ее стоимость максимальна и равна 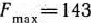 .
.
Положим теперь 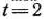 и построим прямую (2 + 2)
и построим прямую (2 + 2)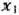 + (13-2)
+ (13-2)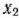 = 4
= 4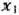 +11
+11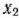 = 44 (число 44 взято произвольно) и вектор
= 44 (число 44 взято произвольно) и вектор 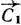 = (4;11). Передвигая построенную прямую в направлении вектора
= (4;11). Передвигая построенную прямую в направлении вектора 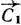 и видим, что последней ее общей точкой с многоугольником решений является точка
и видим, что последней ее общей точкой с многоугольником решений является точка 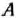 (0; 11). Следовательно, задача, полученная из задачи (69) — (71) при
(0; 11). Следовательно, задача, полученная из задачи (69) — (71) при 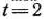 , имеет оптимальный план
, имеет оптимальный план 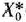 =(0; 11). Это означает, что если цена единицы продукции
=(0; 11). Это означает, что если цена единицы продукции 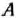 равна 2 + 2=4 руб., а цена единицы продукции
равна 2 + 2=4 руб., а цена единицы продукции 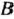 равна 13—2=11 руб., то предприятию также наиболее целесообразно производить 11 ед. продукции вида
равна 13—2=11 руб., то предприятию также наиболее целесообразно производить 11 ед. продукции вида 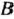 и совсем не производить продукцию вида
и совсем не производить продукцию вида 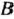 . При таком плане производства продукции ее общая стоимость является максимальной и составляет
. При таком плане производства продукции ее общая стоимость является максимальной и составляет 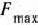 = (2 + 2)-0+(13—2)-11 = 121 руб.
= (2 + 2)-0+(13—2)-11 = 121 руб.
Как видно из рис. 2.7, данный план производства продукции будет оставаться оптимальным для всякого значения 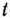 , пока прямая
, пока прямая 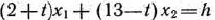 не станет параллельной прямой
не станет параллельной прямой 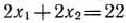 . Это произойдет тогда, когда
. Это произойдет тогда, когда 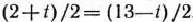 , т.е. при
, т.е. при 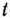 = 5,5. При этом значении
= 5,5. При этом значении 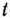 координаты любой точки отрезка
координаты любой точки отрезка 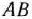 дают оптимальный план задачи (69) — (71).
дают оптимальный план задачи (69) — (71).
Таким образом, для всякого 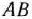 задача (69) — (71)
задача (69) — (71)
имеет оптимальный план 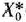 = (0; 11), при котором значение целевой функции (69) есть
= (0; 11), при котором значение целевой функции (69) есть
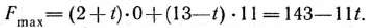
Возьмем теперь какое-нибудь значение параметра 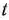 , большее 5,5, например 6. Полагая
, большее 5,5, например 6. Полагая 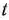 = 6, найдем решение соответствующей задачи (69) — (71). Для этого построим прямую
= 6, найдем решение соответствующей задачи (69) — (71). Для этого построим прямую 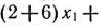
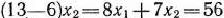 (число 56 взято произвольно) и вектор
(число 56 взято произвольно) и вектор 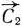 = (8; 7). Передвигая построенную прямую в направлении вектора
= (8; 7). Передвигая построенную прямую в направлении вектора 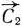 видим, что последней ее общей точкой с многоугольником решений является точка
видим, что последней ее общей точкой с многоугольником решений является точка 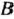 (1; 10). Следовательно, задача, полученная из задачи (69) —(71) при
(1; 10). Следовательно, задача, полученная из задачи (69) —(71) при 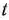 =6, имеет оптимальный план
=6, имеет оптимальный план 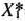 = (1; 10). Это означает, что если цена единицы продукции
= (1; 10). Это означает, что если цена единицы продукции 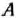 равна 2 + 6 = 8 руб., а цена единицы продукции
равна 2 + 6 = 8 руб., а цена единицы продукции 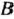 равна 13—6 = 7 руб., то оптимальным планом ее изготовления является план, согласно которому производится одно изделие вида
равна 13—6 = 7 руб., то оптимальным планом ее изготовления является план, согласно которому производится одно изделие вида 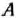 и 10 изделий вида
и 10 изделий вида 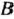 . При этом плане общая стоимость производимой продукции максимальна:
. При этом плане общая стоимость производимой продукции максимальна: 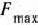 = 8-1+7-10 = 78 руб.
= 8-1+7-10 = 78 руб.
Как видно из рис. 2.7, план 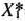 =(l; 10) является оптимальным планом задачи (69) — (71) для всякого
=(l; 10) является оптимальным планом задачи (69) — (71) для всякого 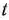 > 5,5 до тех пор, пока прямая
> 5,5 до тех пор, пока прямая
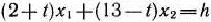
не станет параллельной прямой
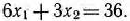
Это произойдет тогда, когда 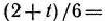
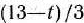 , т. е. при
, т. е. при 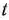 = 8. При этом значении
= 8. При этом значении 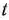 координаты любой точки отрезка
координаты любой точки отрезка 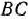 дают оптимальный план задачи (69) — (71).
дают оптимальный план задачи (69) — (71).
Таким образом, для всякого 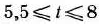 задача (69) —(71) имеет оптимальный план
задача (69) —(71) имеет оптимальный план 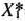 = (1; 10), при котором значение линейной функции (69) составляет
= (1; 10), при котором значение линейной функции (69) составляет
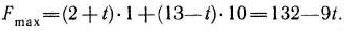
Используя рис. 2.7 и проводя аналогичные рассуждения, получим, что для всякого 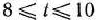 оптимальным планом задачи (69) —(71) является — 8). Это означает, что если цена единицы продукции вида
оптимальным планом задачи (69) —(71) является — 8). Это означает, что если цена единицы продукции вида 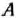 заключена между (или равна) 10 и 12 руб., а единицы продукции
заключена между (или равна) 10 и 12 руб., а единицы продукции 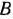 — между (или равна) 3 и 5 руб., то оптимальным планом ее производства является такой план, согласно которому изготовляется 2 ед. продукции вида
— между (или равна) 3 и 5 руб., то оптимальным планом ее производства является такой план, согласно которому изготовляется 2 ед. продукции вида 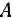 и 12 ед. продукции вида
и 12 ед. продукции вида 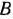 . При этом плане производства продукции ее общая стоимость для каждого значения параметра
. При этом плане производства продукции ее общая стоимость для каждого значения параметра 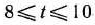 составляет
составляет 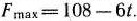 .
.
Таким образом, получаем следующее решение задачи (69) — (71): если 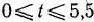 , то оптимальным планом является
, то оптимальным планом является 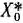 = (0; 11), причем
= (0; 11), причем 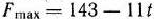 если
если 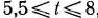 , то оптимальным планом является
, то оптимальным планом является 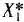 = (1; 10), причем
= (1; 10), причем 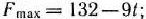 ; наконец, если
; наконец, если 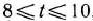 то оптимальный план
то оптимальный план 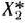 = (2; 8), причем
= (2; 8), причем 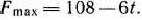
Эта задача взята со страницы решения задач по предмету «математическое программирование»:
Примеры решения задач по математическому программированию
Возможно эти страницы вам будут полезны:
